5.6: Equipartition of Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Energy Modes
Reviewing our work in the previous section in kinetic theory, one might ask, “Where did we use the assumption that the particles are monatomic?” The answer to this question certainly isn’t obvious. Imagine for a moment that we are instead talking about a diatomic gas, where the particles look more like dumbbells than tiny point particles. When one of these particles strikes the wall, one could easily imagine it going from a state of no rotation to one where it is rotating.
Figure 5.6.1 – Diatomic Molecule Bouncing Off a Container Wall
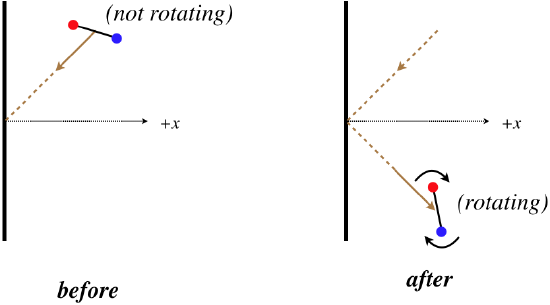
Why would this invalidate the derivation of the previous section? By assumption, the molecule cannot gain or lose energy when it strikes the wall, and we used that fact to show that the speed of the molecule stays constant, but if the molecule can now gain rotational kinetic energy upon striking the wall, then energy conservation requires that the kinetic energy that comes from its linear motion be reduced.
While we can't use the result of our previous work as it stands for diatomic molecules, we can modify things slightly so that we once again get a useful answer. This modification involves the concept of modes available to the energy. In the monatomic case, the motion of the particles involved three independent degrees of freedom – motion along the x, y, and z directions. Looking back at the derivation of the previous section, we see that each of those modes of freedom accounted for an equal amount of internal energy, equal to 12nRT. It turns out that in general the internal energy of a system divides is itself (on average) equally amongst all the available modes. This phenomenon is known as the equipartition of energy theorem.
The best way to track these modes is to imagine energy going into one of them at a time, without changing the energy in the previous ones. So for example, a particle can be moving in the x direction only, and it has a kinetic energy. We could then give it a “kick” in the y direction, and this addition of energy doesn’t change the contribution to the kinetic energy by the motion in the x direction. Once we have kicked it in all 3 directions, there is no other way to kick it that doesn’t give it additional energy in one of the modes already used, so the number of translational modes ends at three.
As we have seen, monatomic gases have only these translational modes, because they have negligible extension in space, which equates to a negligible moment of inertia, which in turn results in zero rotational energy. Diatomic particles clearly do not suffer from having zero moment of inertia, so they do have rotational modes available for kinetic energy. For any three-dimensional object, there are three axes around which any object can rotate, and it is generally convenient to choose their principal axes when discussing such rotational degrees of freedom. For a diatomic molecule which we model as two point particles joined by a rigid rod, these axes look like:
Figure 5.6.2 – Principal Axes of a Diatomic Molecule

Rotation around two of these axes features a non-zero moment of inertia, but around the z-axis rotation is similar to that of a monatomic particle – no extension in space relative to that axis, and therefore zero moment of inertia. Therefore there are really only two rotational modes into which kinetic energy can be distributed for diatomic gases.
Figure 5.6.3 – Two Rotational Modes for Diatomic Particles

So with this rigid-rod model of diatomic particles, the total number of modes into which energy can be distributed is five - three translational and two rotational. With each of these modes getting an average energy of 12kBT, the average energy per particle for this type of ideal gas is:
u=52kBT[rigid-rod model of diatomic ideal gas]
If the particles in the gas are composed of enough atoms that the single axis of symmetry no longer applies, then the I=0 axis no longer exists, and there are three rotational modes available, resulting in an average energy per particle equal to 3kBT. We therefore have the following relationships between internal energies and temperatures for various types of ideal gases:
U=32nRTmonatomicU=52nRTdiatomic with rigid bondsU=62nRTpolyatomic with rigid bonds
Example 5.6.1
One mole of monatomic nitrogen (N) and one mole of diatomic nitrogen (N2) have equal internal energies. How do their rms velocities compare? Assume the mass of N2 is twice that of N, and that N2 can be modeled with a rigid-rod dumbbell.
- Solution
-
With equal internal energies, the two gases cannot have the same temperature. Their temperatures are related by:
U1=32RT1U2=52RT2}⇒T2=35T1
The rms velocity of N2 is:
v2=√3kBT2m2
We can use the temperature relationship above and the mass relationship m2=2m1 to write this rms velocity in terms of the rms velocity of N:
v2=√3kB(35T1)2m1⇒v2=√310√3kBT1m1=√310v1
Vibrational Modes
As we have seen in a previous section, the bonds between atoms can be effectively modeled as springs. If we do this for diatomic particles, then there is yet another independent way to introduce energy into the system – through vibrations of the springs. What is especially interesting about vibrational modes is that they involve not only an additional kinetic energy degree of freedom, but also one associated with potential energy. If we look at a large collection of masses vibrating on springs and do an accounting of the energy, then on average we will find that at any given moment half of the total energy in that collection is in the form of spring potential energy, and half is kinetic energy. Therefore the equipartition of energy theorem for a diatomic molecule that can vibrate allows for two more modes. In this case, we have another relationship between internal energy and temperature:
U=72nRTdiatomic with vibration
So if these modes exist, why even mention the case of "rigid bonds?" A detailed answer to this question lies outside the scope of this course, but the short answer is this: When we get into the realm of the very small (like discussing bonds between individual atoms), we are forced to turn the discussion to an entirely different (more appropriate) model of nature, called quantum theory. In this theory, we find that energy cannot be indefinitely subdivided to smaller and smaller units – it is "quantized." The upshot of this for vibrational modes is that a certain minimum amount of energy is required for this mode to be activated. If this energy is not available (i.e. if the temperature is too low), then we say that the vibrational modes are frozen-out.
It turns out that the amount of energy needed to activate these vibrational modes is quite high, compared to typical temperatures we encounter – this happens at temperatures on the order of thousands of kelvins. Whenever we deal with diatomic gases, we will use the rigid-rod model (and its associated number of available modes) as the default – if the vibrational modes are in play, then it will be made clear that this is the case, either by saying so explicitly, or noting that the temperature of the gas is extremely high.
Digression: More Quantum Weirdness
Lest the reader think that the freezing-out vibrational modes is where the quantum weirdness ends, it should be noted that when the temperature of a diatomic gas gets sufficiently low (roughly double-digit kelvins), the rotational modes also get frozen-out! It might be possible to conceptualize that a molecule requires a certain minimum amount of energy for it to vibrate, but the idea that the same is true for it to rotate is quite bizarre. Quantum theory is full of these truth-is-stranger-than-fiction phenomena.
Molar Heat Capacity
We now return to our discussion of heat. To keep things simple, we will consider the case when two samples are exchanging heat energy (from the hotter to the colder one, obviously), and the volumes of both remain constant. This would obviously be mostly true for solids and liquids (the thermal expansion is a negligible effect), while gases would have to be held in containers with fixed volumes. Under these conditions, all of the heat lost/gained by a sample comes out of/goes into the internal energy of the sample:
Q=ΔU=Uafter−Ubefore
For the sample that gains/loses heat, Q is positive/negative, and the internal energy goes up/down. In our discussion of heat capacity in Section 5.3, we related the change in a sample's temperature to the amount of heat that the same gains or loses. With our results from kinetic theory and the equipartition of energy theorem, we can determine this heat capacity per mole. For example, for a monatomic ideal gas:
Q=ΔU=Δ(32nRT)=n(32R)ΔT
Comparing this to Equation 5.3.6, we see that the molar heat capacity (heat capacity per mole) is a simple constant. It turns out that the assumption we have made (that the gas is confined to a fixed volume) is important to this result. We will look at the more general case later, but for now we will make sure we keep this assumption in mind by adding a subscript to the symbol for the molar heat capacity:
CV=32Rmonatomic ideal gas
Despite the constraints, (the gas must be ideal, it must be monatomic, and the heat transfer must occur with the gas held at constant volume), the result is nonetheless quite remarkable. This same result works for all inert gases such as helium and neon (because they are always monatomic), as well as for other gases that can be found in a monatomic state, like hydrogen and nitrogen.
We can at least account for some of the constraints, by incorporating the number of available modes into the computation of CV:
CV=12R×(numberofavailablemodes)
While this was approached from the case of ideal gases, the result given above is actually more general, since non-ideal gases, liquids, and solids can be taken into account by including the modes associated with interactions of the particles. For example, if we consider a monatomic solid at a high temperature (so that the vibrational modes are not frozen-out), then the lattice structure will result in 6 vibrational modes: 3 kinetic, and 3 potential (springs). With that the case, the molar heat capacity of a monatomic solid is simply 3R. We don’t even care what substance we are talking about!
How do we reconcile this with the fact that we already know that different substances have different specific heat capacities? The answer is that one mole of one substance does not have the same mass as one mole of another. If these two substances have the same number of modes into which energy can be distributed, then they have equal molar heat capacities, but when one wants to convert heat capacity per mole to heat capacity per kilogram, the new constants are no longer equal.
Finally, it should be noted that because CV takes into account the number of modes available for any substance, we have a shorthand for the relationship between the internal energy and the temperature of a sample:
U=nCVT
This applies no matter what type of gas (monatomic, diatomic, etc) we are talking about, because the molar heat capacity (at constant volume) takes into account the number of modes.
Alert
This is an equation of state, relating three state variables to each other (U, n, and T) through a physical constant (CV) that depends only upon the number of modes available to the gas in question. While we got to this point by talking about a process (heat transfer with volume held constant), that process is irrelevant to the meaning of this equation. This is often a point of confusion, and we will return to it later, when we consider processes where volume is not held constant.
Example 5.6.2
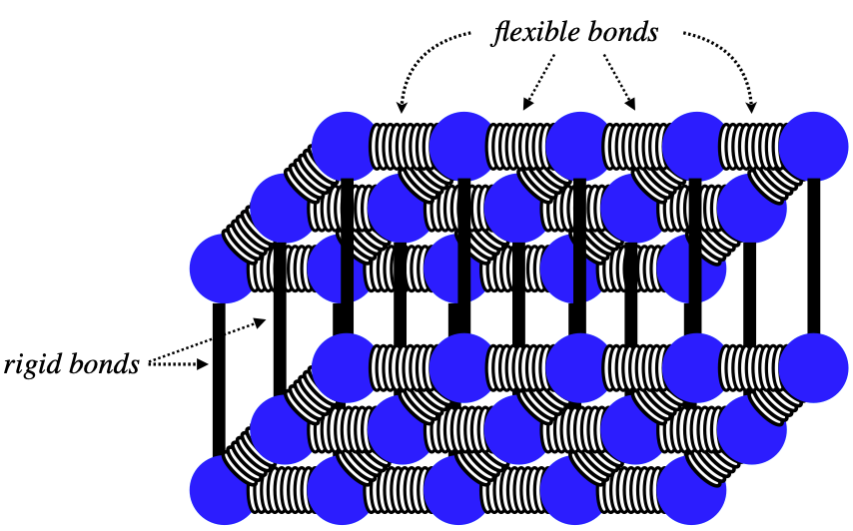
Consider a 1-mole sample of a solid which forms a simple monatomic rectangular lattice, as in the diagram. The types of bonds formed and the temperature of the substance are such that the horizontal bonds are all free to vibrate, while the vertical bonds remain rigid. This sample is brought into thermal contact with 2 moles of a monatomic ideal gas at a different temperature (and the combination of the two are insulated from their surroundings). Assume that the gas and solid neither change phase nor volume during this heat exchange. Find the ratio of the temperature changes (ΔTgas/ΔTsolid) of the gas and solid from the time when they are brought into contact to when they reach thermal equilibrium.
- Solution
-
The heat that enters or exits the solid exits or enters the gas, so they differ only by a sign. Writing the heats in terms of the molar heat capacities and applying this fact gives:
Qintogas=−Qintosolid⇒ngasCgasΔTgas=−nsolidCsolidΔTsolid⇒ΔTgasΔTsolid=−nsolidCsolidngasCgas
The number of moles of each is given, so all that remains is to determine the molar heat capacities, which we can get from Equation 5.6.7. For a monatomic ideal gas the number of modes is 3. This solid has horizontal vibrational degrees of freedom, giving it 4 modes (two KE and two PE). It has no vertical degrees of freedom, nor does it have translational or rotational degrees of freedom, so its total number of modes is 4. Plugging all of this in above (including the numbers of moles of each), we get:
ΔTgasΔTsolid=−(1)(4)(2)(3)=−23
The temperature of the gas changes two-thirds as much as the temperature of the solid, and in the opposite direction.
While we can draw some conclusions about liquids and solids, as we move on into thermodynamics, we are going to focus on ideal gases, for a couple of reasons. First, gases (unlike liquids and solids) can readily change volume, which gives us a great deal more depth of study. And second, we have a state equation we can work with (the ideal gas law) that relates the various state variables.


