5.5: Thermodynamic States of Ideal Gases
( \newcommand{\kernel}{\mathrm{null}\,}\)
State Variables
One of the most important concepts we will use in this course is the idea of a thermodynamic state. There are two key elements to this:
- In thermodynamics, we only deal with equilibrium states. By this we mean that if the physical conditions imposed on the system are not changed, then none of the macroscopically-measurable properties of that state will change. An example in terms of what we have discussed already is the temperature of a sample. We have been assuming that the sample is a uniform temperature throughout its volume. If it were not, then even if we allow no heat to enter or exit the sample (don't change the physical conditions), heat transfers within the sample would still occur, and we would be able to measure temperature changes in various regions of the sample. A sample with differing temperatures occurring in separate regions is not in an equilibrium state.
- For any given equilibrium state, we can completely describe its condition with just a few macroscopically-measurable quantities. So for example, if we have a volume of gas, we can completely define its equilibrium state by measuring its temperature (T), volume (V), and pressure (P). This may not seem to be all that amazing, but the point is that we will see there are many other quantities that can be measured as well (number of particles (N), internal energy (U), etc.) that we can compute from our three measured values, making it unnecessary to measure these new quantities separately. That is, the thermodynamic state is completely defined by the measurements of temperature, volume, and pressure, and every other measurable quantity is then uniquely defined by the fact that we know what state the system is in.
All of the measurable quantities like those mentioned above that define a thermodynamic state are called state variables. What is interesting is that we are not required to measure the three specific state variables mentioned earlier in order to completely define the system – we can mix-and-match them! Using the example above, we could measure the number of particles, the pressure, and the internal energy of the gas, and those measurements would be sufficient to compute the other unmeasured state variables like volume and temperature.
Heat and work are also important concepts in thermodynamics, but they are not state variables! We could have guessed this, since they involve transfers between systems. That is, heat and work are responsible for changing thermodynamic states – they do not serve to define them. As we continue in this subject, we will see how both of these quantities can morph one state into another, thereby changing one or more of the state variables.
Pressure
Many of the state variables mentioned above require no explanation – we have already discussed temperature, and the meanings of particle number and volume are obvious. We will get to internal energy in due course (as well as other state functions not yet mentioned), but pressure requires a brief introduction. Like temperature, the formal definition of pressure is mathematically complicated, but also like temperature, we can get a sense of what it is by the macroscopic effects it causes. Fluids (and in particular, gases, which we will be studying here) consist of many particles moving in a random fashion. When these particles are confined, they bounce off the walls of the container. The transfer of momentum caused by all these collisions is manifested as a force on the confining wall by the fluid. The amount of force is of course a function of how many particles are hitting the surface at any given moment, which means it is proportional to the area of that surface.
We want to define pressure as a property of the fluid, and not dependent upon the container, so we therefore define pressure of the fluid as the amount of force it exerts on a surface per unit area of that surface. What makes pressure tricky is that it takes into account only the disordered (random) motion of the particles. If the fluid is moving in a macroscopically-measurable way (like a river flowing), then the collisions of the particles that result from this macroscopic motion, while it does account for a force, it does not contribute to the pressure of the fluid. For example, your hand is constantly being pressed in all directions from randomly-moving particles in the air, and the force from these collisions can be used to compute the air pressure. But when you hold your hand out the window of your car as the car moves, the force of the air that you feel on your hand is not air pressure. This is because the motion of the air that contributes to this force is not random – it is ordered because it acts in a single direction.
The units of pressure in SI are: [P]=Nm2≡Pa. The renamed units are called Pascals. There are several other units that are used as well, such as psi (lbs per square inch), and torr (aka millimeters of mercury). We will discuss pressure in greater detail, including the origin of this last odd-sounding unit of measurement in Chapter 7.
Equations of State
Given that the state of a system is defined by three state variables, with all the other state variables thereby well-defined, there must be some equations that get us from the values of the state variables we measure to the values of the others. These formulas that relate state variables to each other are called equations of state. For example, the pressure of a state could be computed from (i.e. is a function of) volume, the number of particles, and the temperature:
P=f(V,N,T)
These relationships between state variables (functions) are not the same in all cases – the relationships depend upon the physical system we are talking about. The type of system we will examine extensively (because it is the simplest one for which we can derive useful information, and because it works very well as an approximation) is that of an ideal gas. Physically, an ideal gas is easy to define: It is a system of particles that are free to move (within the confined space defined by the volume), that never interact with each other. This physical system results in an equation of state (called the ideal gas law) that relates the four variables mentioned above through the following functional dependence:
P=f(V,N,T)=NkBTV,kB=1.38×10−23JK
where kB is called the Boltzmann constant. [Yes, this is the same Boltzmann mentioned in a previous section on radiative heat transfer. To say that he was a giant in this field would be an understatement.]
Alert
Note that this equation of state involves temperature as an absolute quantity, rather than just the change of temperature, as we saw previously. For this reason, it is necessary to use an absolute scale (kelvins) rather than a comparative scale (celsius) in calculations involving this formula.
A common alternative to using the particle number as a state variable is using the number of moles (n). A mole of a gas is simply defined as a specific number of particles of that gas. That "specific number" is known as Avogadro's number: NA≡Nn=6.02×1023.
Writing the ideal gas law in terms of the number of moles is therefore a simple conversion:
The constant R is known as the gas constant.
Example 5.5.1
One mole of helium gas is injected into each side of a sliding, airtight lead cylindrical piston of radius 8.00cm that separates two chambers of a sealed cylinder. The outside of the cylinder is insulated everywhere except where noted below. The cylinder and piston have lengths and cross-sectional areas as labeled in the diagram below. The helium in one of the chambers is heated from outside at a rate of 450W, and the helium in the other chamber expels heat into a cool region. The full system eventually comes to steady-state, so that cooler chamber of gas is losing heat at the same rate as the hotter chamber is receiving it. At this steady state, the pressures of the gases in both chambers are equal to 9.00×105Nm2, creating a balance in the forces exerted on the two ends of the piston. The piston therefore remains stationary at an equilibrium point that is a distance x from the end of the cylinder with the chamber receiving the heat. Find the value of x. The thermal conductivity of lead is 35.0WmK.
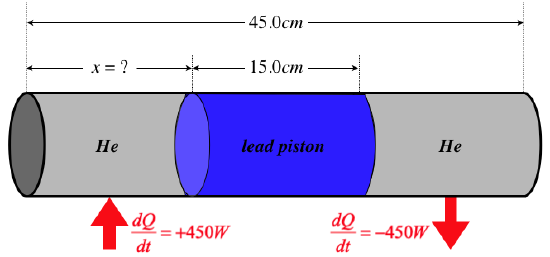
- Solution
-
Heat is being conducted from the left chamber to the right one through the lead piston. We are given the rate of heat transfer, the length of the piston, its cross-sectional area, and the thermal conductivity of lead. We can plug all of these into the steady-state heat equation to find the temperature difference:
dQdt=−kALΔT⇒ΔT=0.150m(35.0WmK)π(0.0800m)2(450W)=95.9K
We are given the pressure of the gases in the two chambers, and the number of moles of gas in each chamber. Using the ideal gas law, we can determine the difference in the volumes of the chambers in terms of the difference in their temperatures:
PV1=nRT1PV2=nRT2}⇒V1−V2=nRP(T1−T2)=(1mol)(8.31JmolK)9.00×105Nm2(95.9K)=885cm3
Now that we know the difference in the two volumes, we can combine this with the sum of the two volumes to get the volume of the left side:
V1+V2=π(8.00cm)2(30.0cm)=6030cm3⇒V1=12[(V1−V2)+(V1+V2)]=12[(885cm3)+(6030cm3)]=3460cm3
The length of this chamber is its volume divided by its area:
x=3460cm3π(8.00cm)2=17.2cm
As with everything else in physics, the idea of an ideal gas is a model. It works pretty well for gases in most real-world circumstances, but it is by no means the only model. Another model treats the gas particles as though they are tiny hard spheres that can bounce off each other. This model may work better in cases of larger molecules and/or higher densities, for example. With a new model comes a new equation of state, and in this case the governing equation is known as the van der Waals equation, which is significantly more complex than the ideal gas law:
The constant b takes into account the "hard sphere" aspect of the particles. The volume available to the gas is the volume of the vessel minus the volume occupied by the particles themselves. The constant a accounts for attractive forces (unsurprisingly called van der Waals forces) between the particles. When the particles attract each other, they don't strike the walls of the container so hard, and the pressure measured by force-per-area on the walls is lower. Notice that taking the limit as a,b→0 returns the equation of state back to the ideal gas law. When the particle radii are negligible and interactions forces vanish, then the conditions for an ideal gas are met.
Kinetic Theory of Gases
One of the most impressive aspects of the study of thermodynamics lies in how it is possible to use a simple microscopic model of how a large number ( 1023) of particles in a gas behave to derive some very specific relationships between macroscopically measurable quantities. We see this in action in the following application of the kinetic theory of gases. We will assume a gas is ideal – that the particles do not interact with each other – and that the gas is trapped within a cubical enclosure.
Figure 5.5.1 – Ideal Gas in a Cubical Container
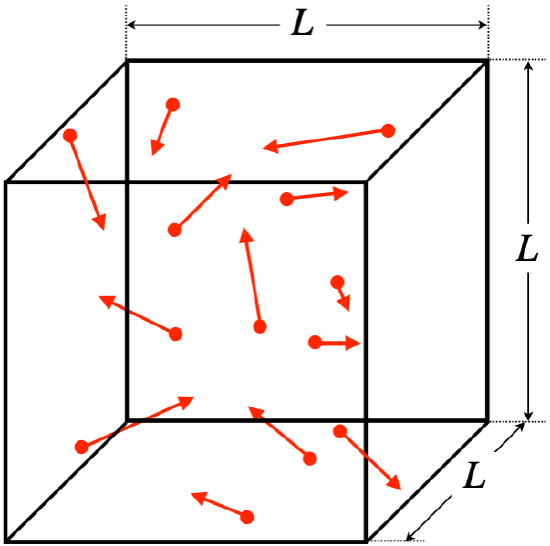
Here are some further assumptions we will make, beyond that of the particles not interacting with each other:
- particles have random positions, speeds, and directions of motion
- no energy lost to the walls (particles collide elastically with walls)
- walls are smooth, so force between particles and wall is perpendicular to wall
- gas is monatomic (individual atoms, not molecules)
We will eventually loosen the last of these constraints, but the others are reasonable and necessary to do the derivation that follows. The assumption that the walls are smooth is not necessary for the final result (nor is the use of a cubical container), but it does make the analysis that follows easier. We will not prove that these simplifying assumptions (smooth surfaces and cubical container) are unnecessary, but at a minimum it should be noted that experimental evidence confirms that the final result works for more general circumstances.
There are literally a trillion-trillion particles in this box, so looking at what they do individually might seem a bit pointless, but in fact we will have the powerful ally of averaging on our side, as you will see. So we forge ahead, looking at the effect of a single particle as it reflects off a wall of the container, hoping to parlay the information we gain into some understanding of pressure, which is manifested as the gas pushing on the walls of the container...
Figure 5.5.2 – Particle Reflection Off Container Wall

A particle that comes into a wall of the container and reflects elastically will exit with the same speed that it has coming in. With the wall being "smooth," there is no force on the particle parallel to the wall, so the component of the particle's velocity parallel to the wall remains unchanged (vy(before)=vy(after)). The elastic collision ensures that the total speed of the particle is unchanged (|→vo|=|→vf|). The combination of these two facts means that the component of the particle's velocity in the direction perpendicular to the wall (depicted in the figure above as the x-axis) is the same before and after the collision with the wall, but in opposite directions.
This particle therefore experiences a force from the wall in the +x-direction that results in a change of momentum equal to 2mvx. Newton's third law tells us that the wall experiences the same force in the −x-direction from the particle. If we average this force over a short time that spans the period from shortly before the collision to shortly after, we get:
(average force on particle over timespan Δt)=1Δttf∫to→Fdt
From the impulse-momentum theorem (a fancy version of Newton's second law), we can replace the time integral of the force with the change in momentum over that timespan:
(average force on particle over timespan Δt)=Δ→pΔt=2mvxΔtˆi
This particle will strike walls other than the two that are perpendicular to the x-axis, but for now we will focus only on the component of the particle's motion along the x-axis. Suppose we wish to know the force that the left wall exerts on this particle averaged over all time. Well, after it bounces off the wall once, it will travel across the box, strike the other wall, and come back again. The x-component of the particle's velocity won't change at the other wall either, so we know exactly how long it takes the particle to make a round trip – the total distance divided by the speed:
time of round trip=2Lvx
With the particle exerting the same force periodically, the average force exerted on this particle over all time is found directly from the last two equations above (we will remove the unit vector from here on, as the direction is clear):
average force on particle over all time=2mvx2L/vx=1Lmv2x
We now note that this is the average force exerted on just one of the many particles present, and with the particles randomly distributed (one of our assumptions), it is clear that the wall is constantly being pelted with particle collisions. The average force exerted on each particle by the wall is equal to the average force exerted on the wall by each particle (Newton's third law), and since some number of the randomly-distributed particles are constantly hitting the wall, there is no reason to expect that the total force on the wall will fluctuate over time. Therefore the force on the wall by the gas is just equal to the sum of the average forces exerted by all N particles:
force on wall by gas=F=1L∑Nmv2x
We now define the pressure of the gas as the force it exerts on a surface per unit area of that surface. In the case of the wall of the container, the area is L2, so we have for the pressure of the gas:
P=FL2=1L3∑Nmv2x=1V∑Nmv2x,
where V is the volume of the cubical container.
Nothing about what we have found here is unique to the walls of the container that are perpendicular to the x-axis, so we also have:
P=1V∑Nmv2y=1V∑Nmv2z
Now we can add the last three equations to each other, and to obtain:
3P=1V∑N(mv2x+mv2y+mv2z)=2V∑N(12mv2)
The particles in this gas do not interact, so the only form of energy they possess is kinetic energy. The sum of the kinetic energies of all the particles is the total internal energy of the gas, which gives us a result that no longer includes any reference to individual particles:
3P=2UV⇒PV=23U
Given that this is an ideal gas which also satisfies the idea gas law, we can write the internal energy in terms of the temperature:
We have been saying for awhile that temperature provides a measure of thermal energy, and now we finally have a formula that gives us exactly how these quantities are related. It is truly remarkable that such specific conclusions can be drawn about the macroscopic state of a gas from such simple assumptions about the microscopic behavior of the particles.
Average Particle Speed in a Gas
We can use Equation 5.5.2 and Equation 5.5.14 to draw another conclusion about the particles in this gas:
U=32NkBT⇒u≡UN=32kBT
This tells us that the average energy per particle u is a constant times the temperature of the gas. Keep in mind that the particles’ motions are randomly (but not uniformly) distributed, so while the average particle has this energy, the actual particles have a range of energies.
With the average kinetic energy per particle, we can determine a sort of average velocity of particles in the gas. There are many sorts of averages, and in this case the type we are referring to is called the root-mean-square, or rms velocity, so-named because its calculation involves taking the square root of the mean of the square of the velocity:
vrms=√⟨v2⟩=√2m√12m⟨v2⟩=√2m√⟨KE⟩=√2m√32kBT=√3kBTm
So the rms speeds of the particles in an ideal gas increase as the square root of the temperature. Also, if the gas is a mixture of particles of different masses, the heavier particles have a lower rms speeds.
Alert
The root-mean-square speed of particles in a gas should not be confused with the "usual" definition of "average," where the speeds of all the particles are added together and the sum is divided by the number of particles. To see the difference, consider a "gas" consisting of two particles, one of which is stationary, and the other moving with a speed of 2v. These particles have an average speed of v, and an rms speed of √2v. The main reason for preferring to use the rms value of speed is that the rms speed is well-defined by the total energy of the gas and the particle number. This is not true of the standard average speed – many average speeds are possible for the same total energy and particle number.


