2.1: Background Material
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\id}{\mathrm{id}} \newcommand{\Span}{\mathrm{span}}
( \newcommand{\kernel}{\mathrm{null}\,}\) \newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}} \newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}} \newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\kernel}{\mathrm{null}\,}
\newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}}
\newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}}
\newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}} \newcommand{\AA}{\unicode[.8,0]{x212B}}
\newcommand{\vectorA}[1]{\vec{#1}} % arrow
\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow
\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vectorC}[1]{\textbf{#1}}
\newcommand{\vectorD}[1]{\overrightarrow{#1}}
\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}
\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\avec}{\mathbf a} \newcommand{\bvec}{\mathbf b} \newcommand{\cvec}{\mathbf c} \newcommand{\dvec}{\mathbf d} \newcommand{\dtil}{\widetilde{\mathbf d}} \newcommand{\evec}{\mathbf e} \newcommand{\fvec}{\mathbf f} \newcommand{\nvec}{\mathbf n} \newcommand{\pvec}{\mathbf p} \newcommand{\qvec}{\mathbf q} \newcommand{\svec}{\mathbf s} \newcommand{\tvec}{\mathbf t} \newcommand{\uvec}{\mathbf u} \newcommand{\vvec}{\mathbf v} \newcommand{\wvec}{\mathbf w} \newcommand{\xvec}{\mathbf x} \newcommand{\yvec}{\mathbf y} \newcommand{\zvec}{\mathbf z} \newcommand{\rvec}{\mathbf r} \newcommand{\mvec}{\mathbf m} \newcommand{\zerovec}{\mathbf 0} \newcommand{\onevec}{\mathbf 1} \newcommand{\real}{\mathbb R} \newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]} \newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]} \newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]} \newcommand{\laspan}[1]{\text{Span}\{#1\}} \newcommand{\bcal}{\cal B} \newcommand{\ccal}{\cal C} \newcommand{\scal}{\cal S} \newcommand{\wcal}{\cal W} \newcommand{\ecal}{\cal E} \newcommand{\coords}[2]{\left\{#1\right\}_{#2}} \newcommand{\gray}[1]{\color{gray}{#1}} \newcommand{\lgray}[1]{\color{lightgray}{#1}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\row}{\text{Row}} \newcommand{\col}{\text{Col}} \renewcommand{\row}{\text{Row}} \newcommand{\nul}{\text{Nul}} \newcommand{\var}{\text{Var}} \newcommand{\corr}{\text{corr}} \newcommand{\len}[1]{\left|#1\right|} \newcommand{\bbar}{\overline{\bvec}} \newcommand{\bhat}{\widehat{\bvec}} \newcommand{\bperp}{\bvec^\perp} \newcommand{\xhat}{\widehat{\xvec}} \newcommand{\vhat}{\widehat{\vvec}} \newcommand{\uhat}{\widehat{\uvec}} \newcommand{\what}{\widehat{\wvec}} \newcommand{\Sighat}{\widehat{\Sigma}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9}Text References
Potentials in General
It's quite possible that you are taking on this week's lab without having seen the topic of electric potential in lecture (or perhaps you have seen it only briefly). Given that this is a lab about electric potential, this might seem to pose a problem, but a brief review of the concept of potential energy from Physics 9A (see the first text reference above) should be sufficient to get you where you need to be for this lab.
In Physics 9A, we linked the ideas of potential energy and force. We found that the force vector at a point in space is determined from the gradient of the potential energy function at that point. In conceptual terms, it works like this: Place yourself at a point in space, and note the potential energy at that position. Then turn around and around, noting the nearby potential energies that you see in every direction. Whichever direction points to the nearby potential energy that is the biggest drop from where you are positioned, that is the direction that the force is exerted.
If you turn to look in a direction in which the potential energy doesn't change at all, then there is no component of the force in that direction. If you start traveling around in the space, always moving in directions where the potential remains the same, then your motion is confined to something called an equipotential surface. With no component of the force acting parallel to the equipotential surface, the total force vector must be perpendicular to it.
Now in Physics 9C, we are using language we did not use in Physics 9A. What we called a "potential energy function" we now refer to as a "scalar field." Note that it means the very same thing – every point in space has associated with it a scalar number. The force vectors we derived from gradients of this field are different at every point in space, so with a vector defined at every point in space, we refer to that as a "vector field." The only other leap we take in Physics 9C is that we use a scalar field that is not potential energy, and a vector field that is not force. Instead, they are electrostatic potential and electric field, respectively. They have different physical meanings and are measured with different units than their 9A counterparts, but the basic ideas are exactly the same: There are equipotential surfaces – surfaces of equal electrostatic potential (voltage) – and a vector (electric) field that is perpendicular to those surfaces everywhere.
Measuring Device for Potential Differences
This week's lab involves a voltage supply connected to a pair of conductors that can come in different shapes. One conductor will be held at a lower potential, and the other at a higher potential. This potential difference will produce an electric field between the two conductors, which is manifested as a continuously-varying electric potential in the space separating them.
We will use a device called a multimeter to measure the potential difference between two points in our apparatus. We will be measuring AC voltages (we will not worry about what "AC" means, or why we use it for this lab) in the 0-20 volt range, so the setting to use on the multimeter is, unsurprisingly, AC 20V (in the "V~" section).
Figure 2.1.1 – Multimeter

The two ports where you plug the probe wires are the black "COM", and the red "V\Omega Hz". In order to measure a potential difference between two points in the apparatus, the leads (probe wires) of the multimeter need to touch those two points.
Apparatus
In order to create a potential field that we can measure with this device, we will connect two conductors to sources of positive and negative charge, and probe the region between them to map surfaces of equal potential. The multimeter can't measure the potentials in the air between the conductors, but it can do it in water, so the two conductors are positioned inside a tray with a thin layer of water in it.
We obviously cannot mark the points in the water that we have probed, so we have a piece of graph paper positioned beneath the transparent tray that we can use to note the location we have probed, and an identical piece of graph paper where we can record the positions of our measurements.
Figure 2.1.2 – The Apparatus

Equipotential Surfaces
At least part of this lab will consist of determining the equipotential surfaces. As with all potentials, we need to set a zero reference point. We know that conductors are equipotentials (i.e. every point on and in a piece of metal is at the same potential), so we will declare one of the two conductors in the apparatus to be at potential V=0. It is standard practice to call such a place the "ground" and it is labeled with a symbol resembling this: 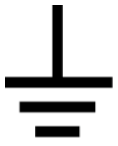 . You will find just such a label on the Pasco box. If you connect the "COM" probe of the multimeter (with an alligator clip) to the conductor connected to this ground, then the other probe will measure the potential of other positions relative to that ground. Note that in the picture above, both probes are touching the same conductor, so the potential difference shown on the multimeter display is zero.
. You will find just such a label on the Pasco box. If you connect the "COM" probe of the multimeter (with an alligator clip) to the conductor connected to this ground, then the other probe will measure the potential of other positions relative to that ground. Note that in the picture above, both probes are touching the same conductor, so the potential difference shown on the multimeter display is zero.
To find surfaces of equal potential (well, as we are confined to measuring in two dimensions, these are actually curved lines rather than surfaces), we only need to choose a potential (say 1 volt), and probe different positions in the water until the multimeter reads 1 volt, and record that position on the transcription paper. With several points recorded, we can "connect-the-dots" with a smooth curve to trace the equipotential. Then we can move on to 2 volts, 3 volts, and so on. With each of the conductors itself being an equipotential, we should expect the equipotential surfaces to gradually "morph" from one conductor to the other.


