1.1: Charges and Static Electric Forces
( \newcommand{\kernel}{\mathrm{null}\,}\)
Fundamental Forces
In Physics 9A, we studied forces. There were many such forces to discuss – gravity, tension, contact (normal), friction, etc. There was one major distinction between gravity and the others – gravity acts at a distance, while all the others required physical contact. In physics we call the different types of forces that act at a distance fundamental forces, inasmuch as all the other forces are built from them. That’s right, ultimately all forces act at a distance – "contact" has no meaning in the microscopic realm of tiny particles. The forces just mentioned, such as tension and friction, are at their core really electrical in nature. There isn’t actually any “contact” made – it’s just that the separation is so small that we can’t see the forces between individual particles with the naked eye, though we can see the aggregate of the forces between many such particles. For example, the force that causes a statically-charged balloon to cling to a wall, or freshly-combed hair to fly apart are forces that act at a distance and can be witnessed with the naked eye.
Given that we are seeing this force act at a distance, we might be inclined to compare it with the only other force we know of that behaves in this manner: gravity. Let’s have a look back at Newton’s law of universal gravitation…
→Fm1onm2=Gm1m2r2(−ˆr)
Let’s break this down, piece-by-piece:
- G – This is just a constant – it ensures that the units come out to what we are accustomed to.
- m1 and m2 – These are the masses of the two gravitating bodies (technically they are either point masses or are spherically-symmetric, but this is quibbling). Mass is both the source of the force and the reason an object reacts to the force. That is, m1 creates the gravity force that m2 feels. When the gravity source m1 is doubled, the force felt by m2 is doubled. When the gravity source m1 is left unchanged but the mass of the object m2 is doubled, the force on that object is again doubled.
- r – This is the separation of the two point masses (or the centers of the two spherical masses). We see that the force gets weaker as the separation increases, according to an inverse-square law. If the separation is doubled, the force gets weaker by a factor of 14. If the separation is tripled, the force gets weaker by a factor of 19, and so on.
- −ˆr – This is the unit vector that indicates the direction of this force. It is defined as pointing away from the source of the force. The minus sign indicates the opposite direction, which is toward the source. The force is acting on the other object, so since the direction of the force on it is toward the gravity source, gravity is said to be an attractive force.
Figure 1.1.1 – Definition of ˆr
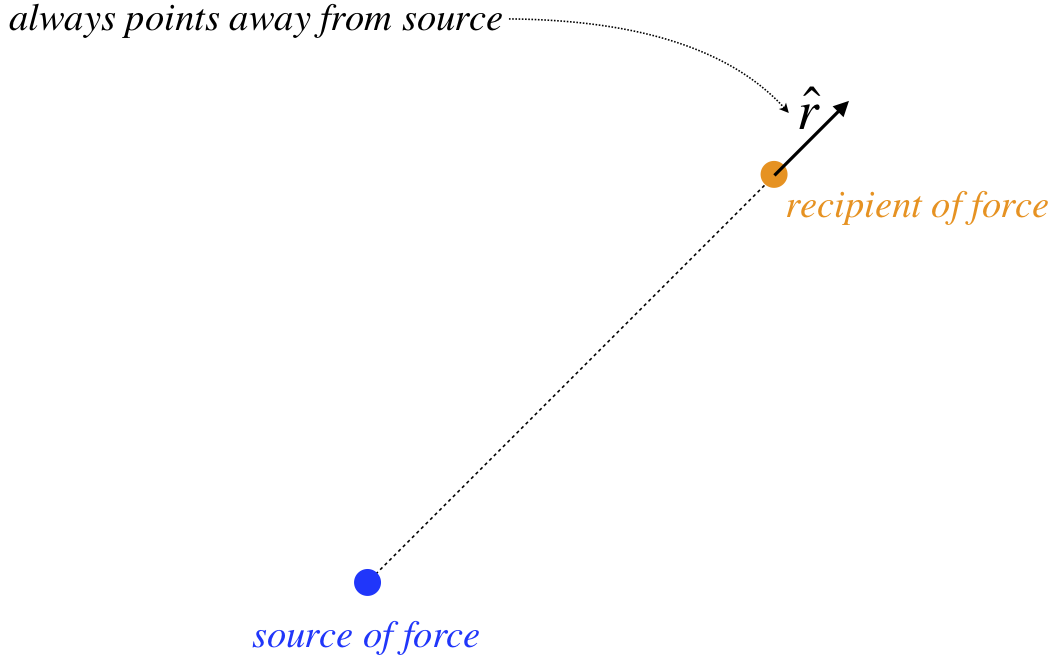
So given what we know about gravitation, we can explore the action-at-a-distance force we observe with static electricity.
Coulomb's Law
First of all, we know that the static electric force is distinctly different from gravity on two different counts. First, the if we have two neutrally-charged particles, we don't see this amount of force, so it can’t be their masses that are responsible for it. And second, besides an attractive force, we also witness a repulsive force, which we do not see for gravity.
A little playing around with the attractive and repulsive forces shows us that there must be two different types of quantities responsible for the force. Gravity had only one type – mass – but this new electric force must have two different types of “mass,” which we refer to as electric charge. The units for this quantity are named after the fellow who did the first detailed exploration of the force, Coulombs (C). When we play around with this force, we find that when two of the same kind of charge are brought together, the force is repulsive, while when we bring different types of charge together, the force is attractive. We summarize this phenomenon with the commonly-used maxim:
unlike charges attract, while like charges repel
For now, we can call these two types of charge whatever we like – black and white, left and right, dumb and dumber – anything that distinguishes them from each other. We’ll come back to a convenient description of the two types shortly.
Next we need to explore the other elements of the force, as we did for gravity. Here are the things we find:
- By holding one charge fixed and varying the other, we can determine the relationship between the amount of charge causing or experiencing the force and the strength of the force. We find that the strength of the force (like gravity) is proportional to both the amount of charge causing the force and the amount of charge feeling the force. So for gravitation we had m1 and m2, and now for electric force we have q1 and q2 (q is the traditional variable used to represent electric charge). The force between two point charges is proportional to the product q1q2.
- We can also test the dependence of the force between two charges on the separation of those charges. Remarkably, we find that when the separation is doubled, the force goes down by a factor of 14, and when it is tripled it goes down by a factor of 19, exactly as it does for gravitation! So the electric force also obeys an inverse-square relation.
Putting these two things together with a constant (similar to G, but with different units) that exists to make our units work out correctly, we end up with a magnitude of the electric force that obeys:
|→Fq1onq2|=kq1q2r2,where:k≡9.0×109Nm2C2
All that is missing is our vector direction, which we covered nicely with the −ˆr in the case of gravity. But what do we do here, append a little explanation, “repulsive if both charges are the same type, attractive if they are not?” That is not very satisfying mathematically, and it turns out there is a nice, elegant solution: Call one of the types of charge “positive,” and the other “negative,” and write the force vector as follows:
The ˆr means the same as it did before – it points away from the charge causing the force. But notice what our mathematical definition of positive and negative charges accomplishes: If both charges are the same type, then their product is positive, and the force points in the direction of ˆr, which is repulsive (object is pushed away from the source). But if the charges have opposite signs, then their product is negative, and the force direction is −ˆr, resulting in an attractive force. The above force law is called Coulomb’s law.
As with any forces, when there is more than one electrical force on a charge, the total force is computed by adding the individual forces like vectors. We call this principle superposition.
Example 1.1.1
Four identical charges are located at the corners of a square. The force exerted between two charges at opposite corners is 1N. Find the magnitude of the net force on one of the charges.
- Solution
-
First of all, with the charges being identical, the force between any pair of charges is repulsive. In the diagram below, we have labeled the length of each side of the square, and drawn in the three forces on one of the charges, one of which is due to the diagonal charge, and the other two are unknown, but they are equal in magnitude to each other, and are greater than 1.00N because the charges are identical and the adjacent charges are closer than the diagonal charge.
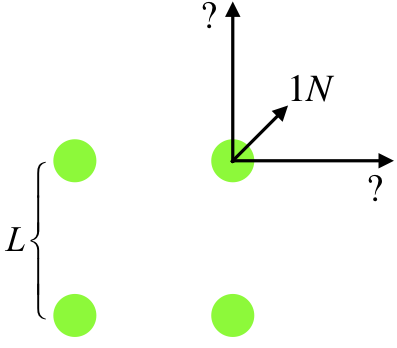
Writing the Coulomb force between the diagonal charges in terms of the charges (which we'll call Q), and the separation (which across a square of side L is √2L), we can get the magnitude of the force exerted between adjacent charges, which are separated by a distance L:
1.00N=kQ2(√2L)2⇒kQ2L2=2.00N
Now we superpose the three forces (i.e. add them like vectors) to get the magnitude of the net force, Fortunately this is easy, as the direction of the sum of the vertical and and horizontal force vectors points in the same direction as the diagonal force vector:
Fnet=√(2N)2+(2N)2+1N=3.83N
Properties of Electric Charge
There are just a few things we need to say about electric charge before we move on.
- There exists a minimum “fundamental” unit of charge, below which charge cannot be subdivided. This amount is a very small number of Coulombs:
e≡1.6×10−19C
This is the amount of charge that resides on the tiny particles we have heard about that reside within atoms: protons (+ charges), and electrons (– charges). We have Benjamin Franklin to "thank" for these sign conventions (we'll see that this choice is a bit of a pain). Despite the fact that charges come in integer numbers, we will treat them as continuous values.
- Electric charge is conserved. We know from our study of energy what this means – it can neither be created nor destroyed. It doesn’t mean that the particles on which that charge resides cannot change into other types of particles (e.g. neutron → proton + electron + antineutrinos), just that when the particles do change, the new particles’ charges have to add up to the same charge the original particle started with.
- When we deal with charges in the real world, they are usually residing on some substance. We can very crudely divide materials into two types of substances (actually there are many variations in-between, but for now this distinction will do):
- conductors (think “metals”) – charges are free to move around on (and through) these substances
- insulators (think “non-metals”) – charges are locked into place and cannot move around
As innocuous as these distinctions may seem, we will see that they lead to some profound properties.


