1.4: Dipoles
( \newcommand{\kernel}{\mathrm{null}\,}\)
Definition of a Dipole
Whenever possible, it is a good idea to “package” common physical situations into models that we can re-use without having to always reinvent the wheel. We actually discussed this to some extent in the previous section, in the context of solving for the field of an infinite line or plane of charge. We know well how to deal with single point charges, but of course physical systems rarely behave in such a simple way. What we are going to look at here is a model for two point charges that are equal in magnitude and opposite in sign. The reason this is such an important package to develop is that it appears so much in nature, in the form of neutrally-charged molecules.
Consider two equal point charges, one positive, and the other negative, that are held rigidly at a fixed separation distance (if you like, you can imagine a tiny rigid rod holding them at fixed relative positions). We have already seen what the field of such a dipole configuration looks like, in Figure 1.2.2. We could forever treat such a configuration as a combination of two point particles, but it is helpful to package them so that we can treat them as a single entity and not have to go back and recalculate things. To that end, we define a vector quantity known as an electric dipole moment as follows:
Figure 1.4.1 – Electric Dipole Moment
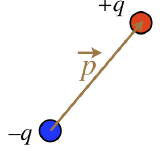
The magnitude of the dipole moment is defined as the product of the absolute value of one of the two charges, multiplied by the distance separating the two charges:
|→p|≡qd
The direction of the dipole moment is that it points from the negative charge to the positive charge.
Alert
Chemists typically define the dipole moment as pointing in the opposite direction. When creating a "package" for later use, how you define it is up to you. We will see that there are compelling reasons (at least in physics applications) for defining it as above.
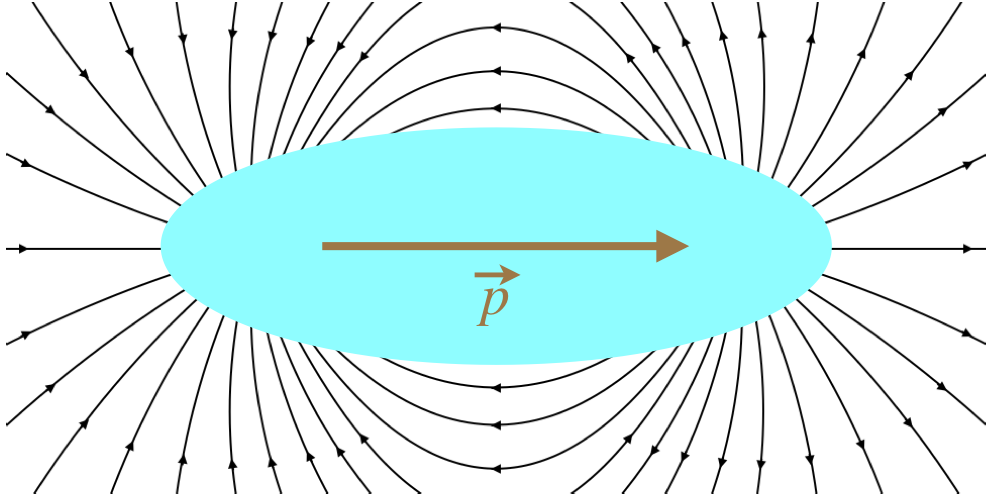
Note that the dipole moment is not the same as the dipole electric field. It may seem funny to even mention this, as these two quantities are not even close to being the same, but it does come up. One place where it gets confusing is that the dipole moment points in the opposite direction as the electric field between the two charges. But as we are forming a package with these two charges, what happens between them is of no consequence. When it comes to the direction of the dipole field, the dipole moment direction makes perfect sense.
Figure 1.4.2 – Field of a Dipole
Dipoles in External Fields
We consider now the effect that a uniform electric field has on a dipole. Note that while we will be assuming a uniform field, in reality we mean that the amount that the external field changes across the length of the dipole is negligible. Also, as will generally be the case going forward, when we draw a diagram of a uniform field, we will represent it with a set of parallel field lines.
Figure 1.4.3 – Dipole in a Uniform Field
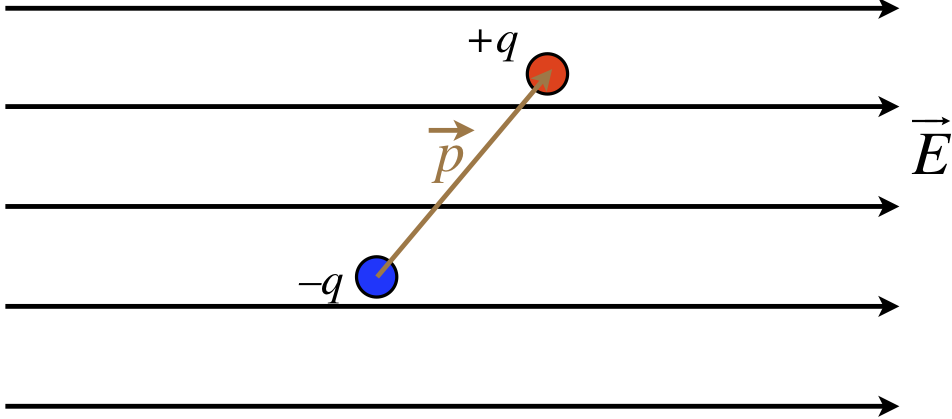
We begin by considering the force on the dipole. Certainly each individual charge feels a new force from the field, but the charges are equal in magnitude, and the forces act in opposite directions, so the net force on it is zero.
Alert
If the field is not uniform, then the dipole can experience a net force! This might seem odd, given that the "package" of two charges is neutrally-charged, but it is an important physical effect to be aware of (we will discuss it in more detail later).
With no net force, the center of mass of the dipole will not accelerate, but there will clearly be a torque exerted on this object. We can introduce a coordinate system above, and determine what this torque is, in terms of the field and dipole moment.
Figure 1.4.4 – Torque on a Dipole
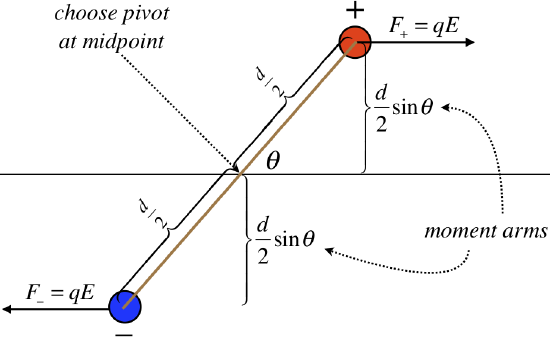
Multiplying the forces by the moment arms, and summing, we find that the magnitude of the torque on this dipole is:
τ=2[qEd2sinθ]=qdEsinθ
The magnitude of the dipole moment appears in the equation, as does the strength of the electric field, and the sine of the angle between them. This would suggest a connection to the cross product of the dipole moment and the electric field vector. Looking at the diagram, we see that the torque will cause clockwise rotational acceleration, which means that the torque vector points into the page. Indeed, the right-hand-rule applied to the cross product of →p and →E results in a vector that points into the page, so we conclude:
→τ=→p×→E
Example 1.4.1
A dipole is a distance r from an infinitely-long line of negative charge of density λ.
- The dipole moment →p is parallel to the line of charge. Find the magnitude of the torque on the dipole in terms of r, →p, and λ.
- The dipole moment is now pointing directly at the line of charge (perpendicular to it). Is there a net force on the dipole, and if so, is it toward or away from the line of charge?
- Solution
-
a. The field is the same strength at both ends of the dipole, so we can just use the torque equation. The field is axially inward to the line of charge, which means that it is perpendicular to the dipole moment, so plugging in the field of the long line of charge, we get:
τ=pEsin90o=2kpλr
b. The field from the long line of charge is not uniform – it is stronger closer to the line. Therefore the "front" of the dipole, which is closer to the line of charge, feels a strong force than the "rear." The line of charge is negative, which means the front of the dipole (which is the positive charge) is attracted more than the rear is repulsed, and the dipole feels a net force toward the line of charge.
He have talked about force and torque, so all that remains from classical mechanics to consider is potential energy. Why should there be potential energy at all? Well, suppose we release the dipole in the diagram above from rest. Clearly it will begin to rotate, which means it will gain kinetic energy. This energy must come from somewhere, and in fact it comes from the work done by the electric field. But the electric field exerts a conservative force, so we can also express it in terms of a potential energy. The change in potential energy due to a conservative force is the negative of the work done by that force. So let's consider the work done by the electric force on the charges of the dipole as the dipole rotates (note, there is no net force on the dipole as a whole, so the movement of its center of mass doesn't change the potential energy).
Figure 1.4.5 – Potential Energy Change for a Rotating Dipole
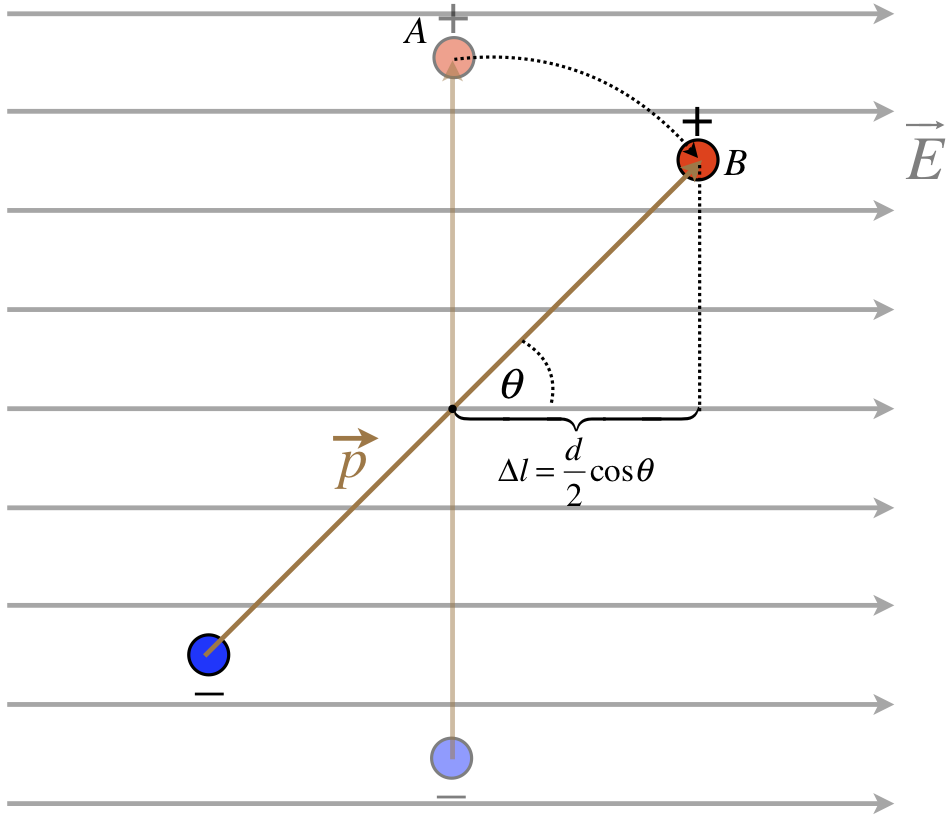
Only the displacement of each charge along the direction of the force (which is parallel to the electric field) counts toward the work done. The force on each charge has a magnitude of qE, and the force acts in the direction of the displacement for both charges (remember the force on the negative charge is the opposite direction of the field), which makes the work done positive, and the change in potential energy negative. For both charges charge we therefore have:
ΔUdipole=−2W(A→B)=−2FΔl=−2(qE)(d2cosθ)=−(qd)Ecosθ
While the torque evoked the idea of a cross product, the potential energy screams out dot product. If we follow a typical convention and define the zero potential energy exist in the configuration when the dipole is perpendicular to the field, then we have:
Udipole=−→p⋅→E
Note that the energy is a minimum when the dipole moment aligns with the external electric field.
The Dipole Field
If we are to treat dipoles as "packages," then we have to stop looking at them so closely. Okay, so what do they look like if we look at them from far away? Well, to determine this, we need to look at them as two charges (sigh, again), and look at the field they create at a distance much greater than their separation, d. As with the results above, we want our final answer in terms of the dipole moment, not the charge and separation.
We'll start with a simple part of the field – along the axis defined by the dipole moment. Clearly the field points out of the dipole on one end, and into it on the other, following the direction of the dipole moment. For this calculation, we will place both charges on the x−axis, equal distances from the origin, with the positive charge on the positive side of the origin. Along the axis a distance r from the origin (on the positive side of the origin), the field of the negative charge is a bit weaker than the field of the positive charge, as it is farther away by a distance d. The exact field at this point is:
→E=k(−q)(r+d2)2ˆi+k(+q)(r−d2)2ˆi
If we get a common denominator and do a bunch of algebra, we wind up with this:
→E=32kqdr(4r2−d2)2ˆi
Now let's rearrange things a bit. First, we'll replace the quantity qd with the magnitude of the electric dipole moment, p. Next, we'll divide both the numerator and denominator by r4:
→E=32kpr−3(4−d2r2)2ˆi
Up to now, we have made no approximations. So finally we invoke what we stated at the outset – let's look at positions that are very far from the dipole compared to the separation of the charges. With this assumption, the ratio of d to r is very small, and the square of that ratio is even smaller, so we treat it as negligible, giving:
→E=2kpr3ˆi
We find the interesting result that while the field of a monopole (point charge) falls-off as 1/r2, the field of a dipole (at least along the axis of the dipole moment, and as it turns out, everywhere else – see below) falls off faster – as 1/r3. This actually should not surprise us, if we take another look at the dipole field in Figure 1.2.2. We know that the field gets weaker as the field lines diverge from each other. The field lines of a monopole emanate straight out of the charge, and diverge at a constant angle. Along the axis of the dipole, we can see that the field lines bend away from the axis, which means they diverge faster than the monopole case, so the field gets weaker faster.
It is a little bit more complicated to work out the field of the dipole off the axis, and we won't go into the details of this derivation, but the final result is:
Example 1.4.2
Show that the general formula for the dipole field yields the proper field along the axis of the dipole.
- Solution
-
Along the axis of the dipole, the position vector (and therefore the position unit vector) for the field is parallel to the dipole vector. If the position of the field is on the positive side of the dipole, then the position unit vector points in the same direction, and:
→p⋅ˆr=|→p||ˆr|cos0o=p⇒3(→p⋅ˆr)ˆr=3pˆr=3→p
Plugging this back into the general formula gives the result on the axis.


