3.4: Matter Has Wave Properties, Too!

What About Known Particles?

Okay, so we have established that light can behave as a particle (photon) or as a wave (Maxwell).  It seems as though how it behaves simply depends upon the context we put it into.  If we do typical optics experiments (polaroids, double slit interference, etc.) then light is clearly a wave, but if we do the experiments of the 20th century (blackbody radiation curve, photoelectric effect, Compton scattering), then it acts very much like a particle.  But how can a single entity simultaneously act like two such opposite phenomena?  Is light localized into little packets of energy, or is it spread out and able to exhibit interference?  IT CAN’T BE BOTH!!

Okay, let's set aside this conundrum for a moment and change gears. If light, which we previously "knew" to be a wave, can suddenly start showing particle properties, might we not see the wave properties for things we have always "known" to be particles? Well, in fact, just such an experiment has been performed by Davisson and Germer in 1927. They fired electrons through a lattice of nickel atoms, and found that the pattern they formed on the other side looked just like that of a diffraction grating.  So not only do "known" waves have particle properties like momentum and localized energy, but "known" particles have wave properties like interference!

de Broglie's Idea

Unlike the case of Planck, who essentially worked backwards from puzzling experimental data, Louis de Broglie anticipated the results of Davisson and Germer, when a few years before their experiment, he hypothesized that if light can behave as both wave and particle, why not matter? But he did more than just say that this could be true, he found a common element between the two cases, and used it to make a prediction. It goes like this...

Light carries energy, and has momentum.  According to what we learned in relativity, light has no mass, so these quantities are linked by:

\[E^2=p^2c^2+m^2c^4~~~\Rightarrow~~~E=pc\]

But now we also know that the energy of a quantum of light is directly related to its frequency, so we can relate the momentum of light to its wavelength:

\[p=\frac{E}{c}=\frac{hf}{c}=\frac{h}{\lambda}\]

de Broglie speculated that perhaps the link between momentum and wavelength is a fundamental one, and posited that it might extend over to particles. So if we fire a beam of electrons at a known speed (or equivalently, with a known kinetic energy), then we can compute the wavelength they will exhibit in a diffraction pattern.  So for a diffraction grating with slit separations equal to \(d\), we should see "bright fringes" (lots of electron landings) at angles \(\theta_m\) that satisfy:

\[d\sin\theta=\lambda~,~~2\lambda~,~~3\lambda~,\dots~~~~~\text{where:}~~~\lambda = \frac{h}{p_e}=\frac{h}{m_ev}=\frac{h}{\sqrt{2mE}}\]

This wavelength is known as the de Broglie wavelength, and indeed we found that this explains the results of the Davisson-Germer experiment.

Alert

We have now seen two differently-defined wavelengths for matter – Compton and de Broglie wavelengths.  Don't confuse these with each other! The Compton wavelength is defined purely by the mass of the particle (so it is a fixed number), while the de Broglie wavelength is defined by a particle's momentum (so it changes, depending on how fast the particle is moving).

While both light and matter exhibit these wave & particle properties, for the sake of keeping clear what we are talking about, when we are talking about the wave properties of matter (which we will do a lot from now on), we will avoid confusion by referring to the waves associated with matter as matter waves. The reader is cautioned against misinterpreting this moniker, however. "Water waves" are waves for which the medium is water, and "string waves" indicate that the medium is string. It is incorrect, however, to interpret "matter waves" as indicating that the waves are made out of matter. Light travels through no medium whatsoever (there is no luminiferous aether), and the same is true of matter waves.

An Important Feature of Matter Waves

When we discussed double slit interference for the first time, we found that we can only see a significant interference pattern (many bright and dark fringes) if the wavelength of the light is much smaller than the slit separation.  This is because the maximum-order of bright fringe is limited by the fact that \(\sin\theta\le 1\):

\[d\sin\theta=m\lambda~~~\Rightarrow~~~m_{max}\le\frac{d\sin\theta_{max}}{\lambda}=\frac{d}{\lambda}\]

So if we wish to probe very small dimensions (characterized here by the slit separation), we can't get much information about it if the slit separation is smaller than the wavelength of the light, since we won't be able to make out any features – we can't tell how far apart the slits are if they are so close that no interference pattern is present. This means that we can only make out smaller features (like the separations of atoms in a crystal) with light that has sufficiently-short wavelengths. But very short wavelength light is also very energetic. The wavelength of a particle with mass is significantly shorter than the wavelength of a photon of equal kinetic energy.  For example, to look at features on the scale of nanometers (large molecules) requires wavelengths in the same range (about \(10^{-9} meters\)).  To do this with light requires an energy per photon of:

\[E=pc=\frac{hc}{\lambda}=\frac{\left(6.63\times 10^{-34}Js\right)\left(3\times 10^8\frac{m}{s}\right)}{10^{-9}m}=2.0\times 10^{-16}J\]

An electron of the same wavelength has a kinetic energy of:

\[E=\frac{p^2}{2m_e}=\frac{h^2}{2\lambda^2 m_e}=\frac{\left(6.63\times 10^{-34}Js\right)^2}{2\left(10^{-9}m\right)^2\left(9.11\times 10^{-31}kg\right)}=2.4\times 10^{-19}J\]

Almost 1000 times as much energy is needed for x-rays than is needed for an electron beam, to achieve the same resolution.

Richard Feynman's Question

What follows is a nice description of our confusing mess as first described by a physicist named Richard Feynman. Consider firing electrons at a double-slit apparatus, with one of the two slits blocked. With one path to the screen, we see a distribution of electron-caused dots on the screen exactly as we would expect – in a cluster centered directly opposite the slit. Next the slits are reversed – the previously-closed slit is opened, and the previous open slit is closed. Unsurprisingly, we see the same result – a cluster of dots on the screen centered across from the slit.

Figure 3.4.1 – Electrons Through a Double Slit with One Slit Blocked

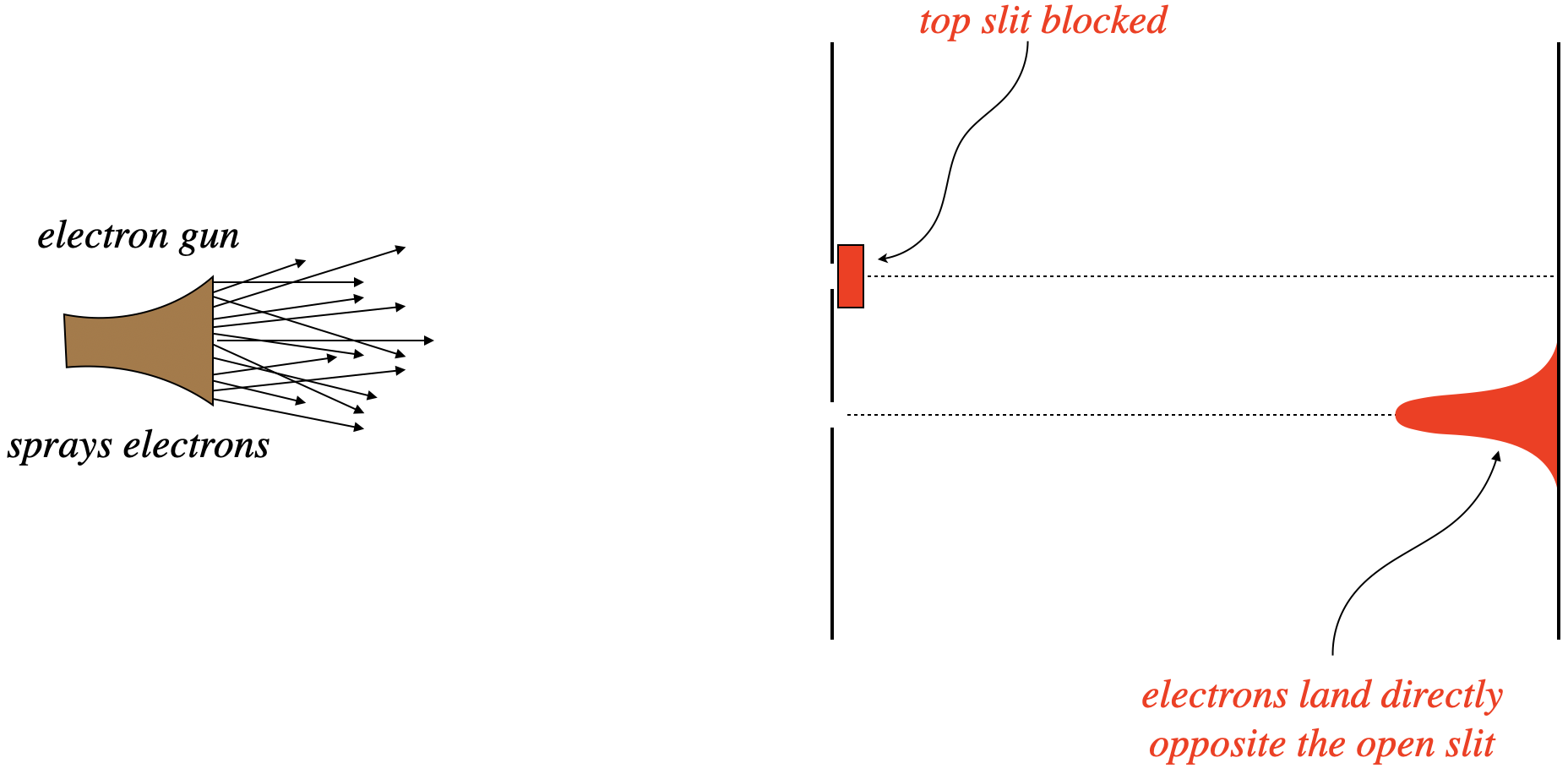
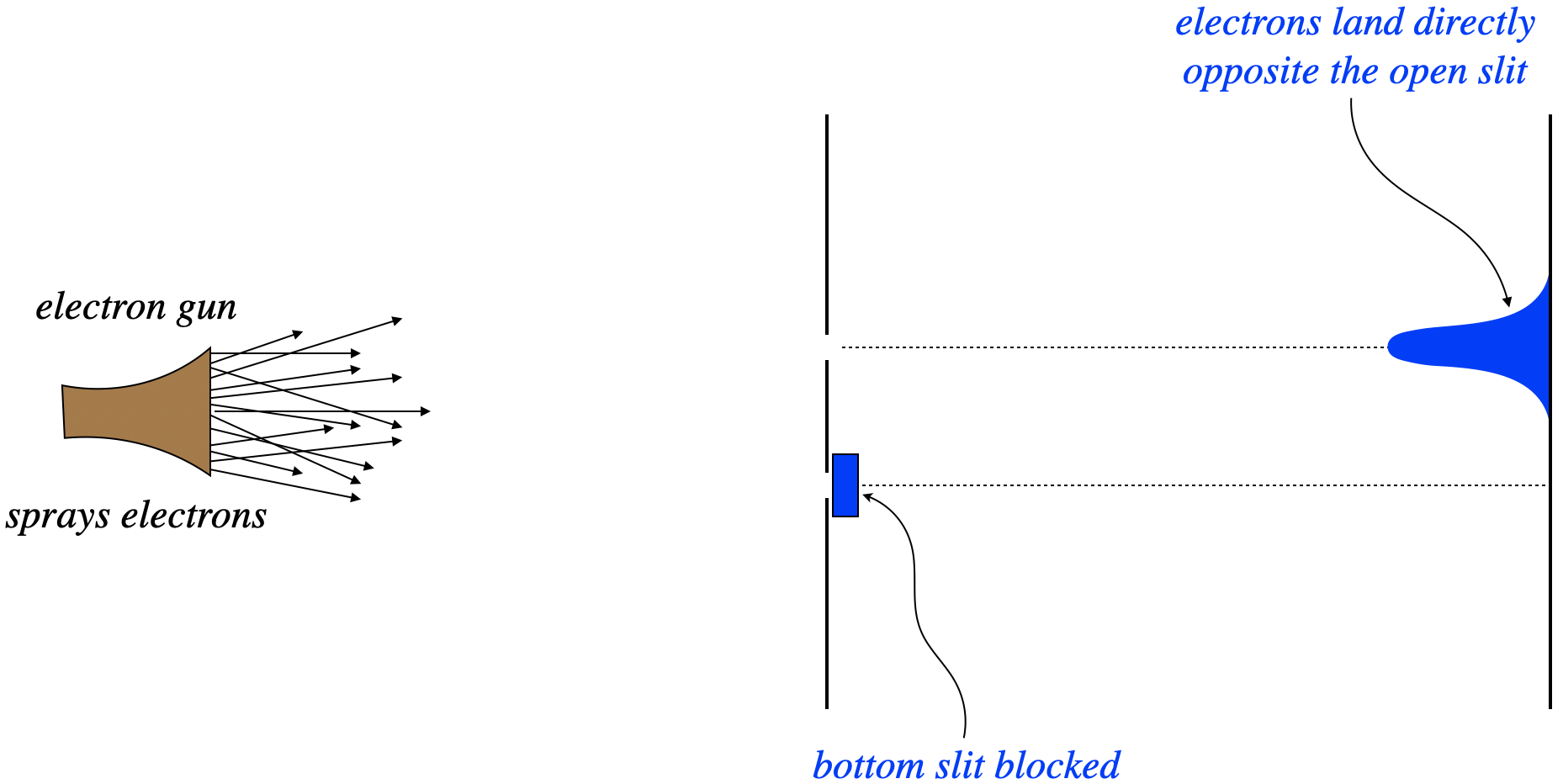
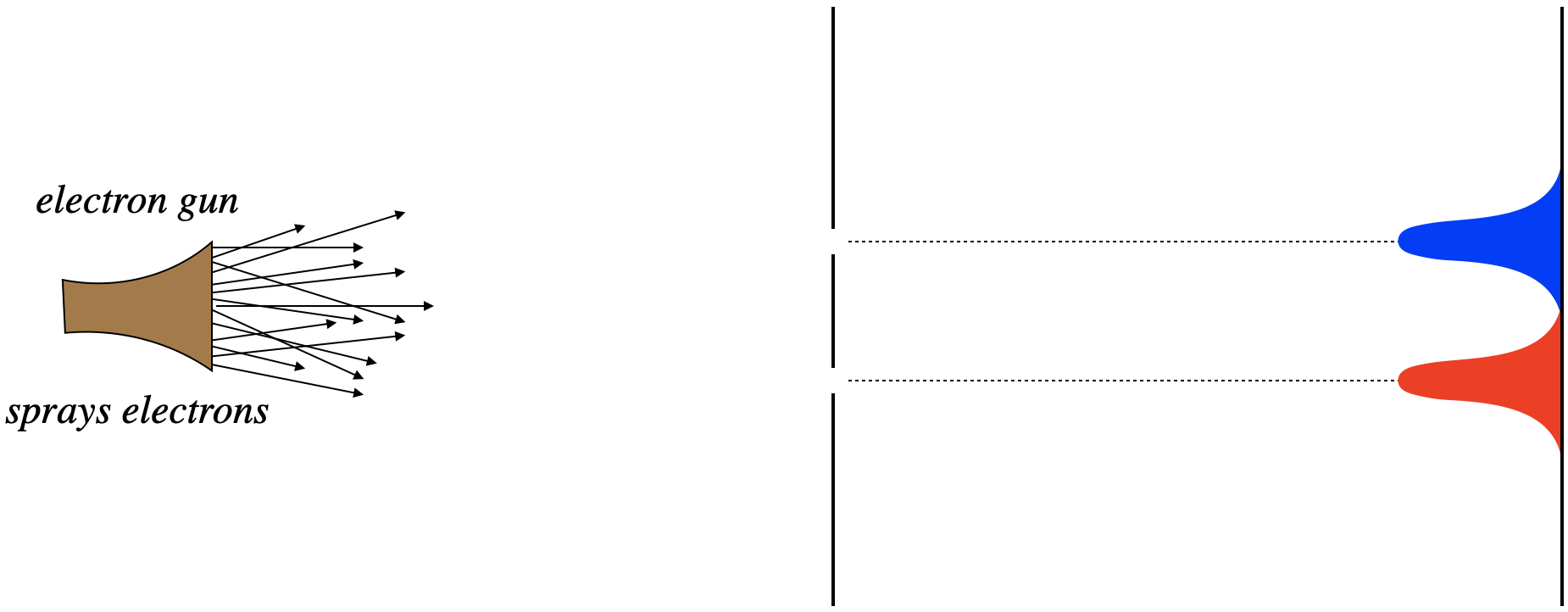
Given these results, the natural prediction of what happens when both slits are open is that we see both of the patterns we saw previously, at the same time. All the electrons that pass through the top slit should end up across from it, and all of those that pass through the bottom slit end up across that that slit.

Figure 3.4.2 – Electrons Through a Double Slit with Both Slits Open (Expected)

But the result (if the slits are spaced appropriately), is completely different. Rather than clusters of dots across from the slits, there are virtually no dots at all, and places where we expected very few dots are quite populous. In short, we see an interference pattern!

Figure 6.1.3 – Electrons Through a Double Slit with Both Slits Open (Actual)

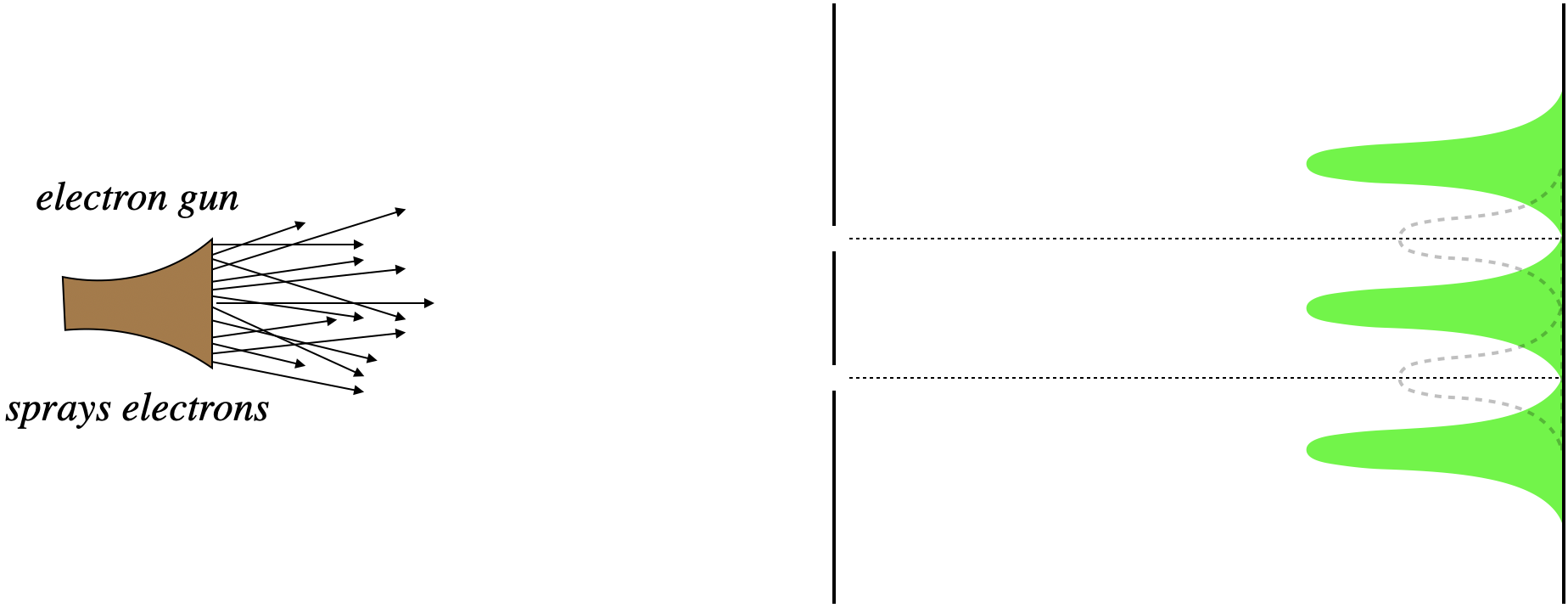
The first attempt to explain this is naturally to say that the electrons are interacting with each other after they pass through the slits. But even if the electrons are sent through one at a time, the accumulated landings follow this pattern.So Feynman's puzzling question is, "How does an electron, while going through the bottom slit, know whether or not the top slit is open?" If it is open, it's destination is different than if it is closed, but how can it tell where it is "supposed" to go? Like the case of photons, we can only conclude that the electron somehow passes through both slits at once, in the form of a wave. We will discuss this further in the next section.