3.5: Summarizing this Wave/Particle Mess

Wave-Particle Duality

Okay, so we have established that light can behave as a particle (photon) or as a wave (Maxwell).  It seems as though how it behaves simply depends upon the context we put it into.  If we do typical optics experiments (polaroids, double slit interference, etc.) then light clearly behaves like a wave, but if we do experiments related to the interaction of light with matter (blackbody radiation curve, photoelectric effect, Compton scattering), then it acts very much like a particle.  But how can a single entity simultaneously act like two such opposite phenomena?  Is light localized into little packets of energy, or is it spread out and able to exhibit interference?  IT CAN’T BE BOTH!!  This mystery is what physicists refer to as wave-particle duality.  Giving it a name helps us manage our sanity, as it fools us into thinking it is reasonable.  Okay, so we have actually done more than just give it a name, but the reader should understand at the outset that ultimately this is just another one of the incomprehensible wonders that comes from modern physics.

Very Low Intensity Double Slit Interference

It seems like there has to be some way to test both the particle and wave nature of light with the same experiment.  What most defines the wave nature of light is the phenomenon of interference. This plays no role in any of the experiments we have discussed so far that show the particle nature of light, so let's go back to an interference experiment and see if we can throw-in the particle nature.

The explanation of the photoelectric effect states that light intensity is manifested in the number of photons passing per second.  This means that we could, in principle, lower the intensity of the light to the point where only one individual "packet of light" is present.  If we fire this photon at a screen where it is detected, it will only make a single dot.  If we fire it at a double slit, assuming it makes it through to the other side (i.e. doesn't make a dot on the screen where the slits are cut out), then when it hits the back screen, do we see an interference pattern? The answer is "No, it makes a dot on that screen as well." So that settles it – photons must be particles! Not so fast.  We still have to answer where the interference pattern comes from when we should a lot of photons. Maybe they bounce off each other somehow, so that a lot land in some places (bright fringes) and none land in others (dark fringes)?  We can test this idea by sending lots of photons, one at a time. Every time a dot appears, we send another single photon. These photons don't land in the same place every time, but they don't land perfectly randomly, either – they form a pattern... a familiar pattern. Below is a simulation of what is seen, sped up many times the actual one-dot-at-a-time rate.

Figure 3.5.1 – One-Photon-at-a-Time Through a Double Slit

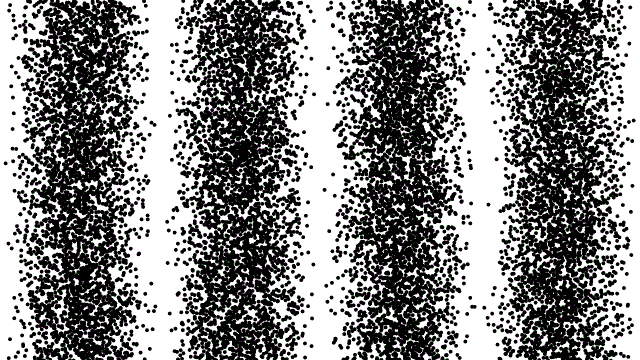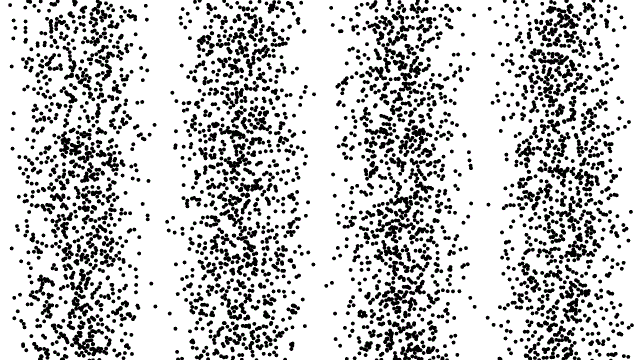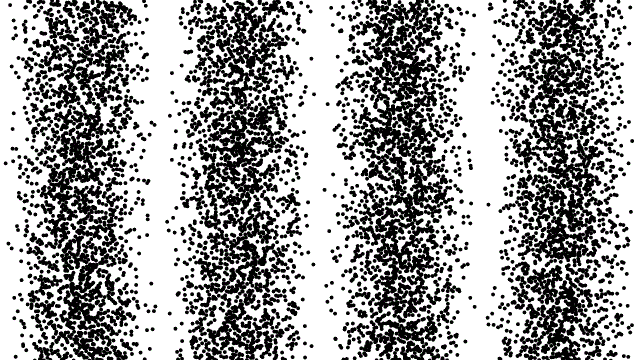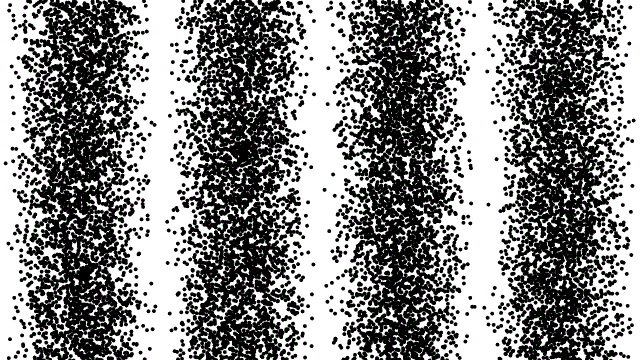
Our perfectly reasonable idea that light as particles can exhibit wavelike interference behavior by having particles interact with each other fails miserably! The photons travel alone, free from being affected by any other photons, and yet when all the photon landings are aggregated, the interference pattern emerges! We are foiled once again from definitively showing that light is either a particle or a wave.

The only explanation left to us requires a statistical argument: The pattern shown on the screen must represent a probability distribution for the landing points of the individual photons. The places dense with dots are places where a single photon has a very high probability of landing, while those less dense are less probable landing points (and those with no dots have zero probability of a photon landing there!).

The strange part of all this is that these probabilities appear to obey wave mechanics. That is, when we change the spacing between the slits, or the wavelength of the photons, the pattern changes in a manner that is precisely consistent with wave interference. This puzzle of something as abstractly mathematical as probabilities being subject to the rules that exist for waves is one of the most fundamental aspects of what is known as quantum theory. As we will see, wave-particle duality is not the only place where something we expect to be smooth and continuous (like a light wave's interference pattern) turns out to be discrete (like a single dot on a screen). This probabilistic/statistical interplay between what we see in the big picture as continuous, and what we see in the small scale as discrete leads us to invent new language to describe quantities that doesn't imbue them with inherently "particle" or "wave" properties. We then generically refer to these quantities as "quanta".

We say that until we actually force a quantum to reveal its particle properties (like a dot on a screen), it exists as a mysterious entity that is spread throughout space, and propagates & interferes with itself like a wave. This mysterious wave entity carries with it information about the probabilities of various measurements, most notably the location of the particle.

What if We "Peek"?

In an attempt to solve the puzzle of the double slit from the previous section, we might try to simply watch the electrons as they pass through the slits. To do this, let’s put a bright light source between the slits, so that when electrons pass, by the light scatters off them and we see a small flash of light coming from the location of the electron, thereby telling us which slit it went through.

Figure 3.5.2 – Watching the Electrons as They Pass Through the Slits

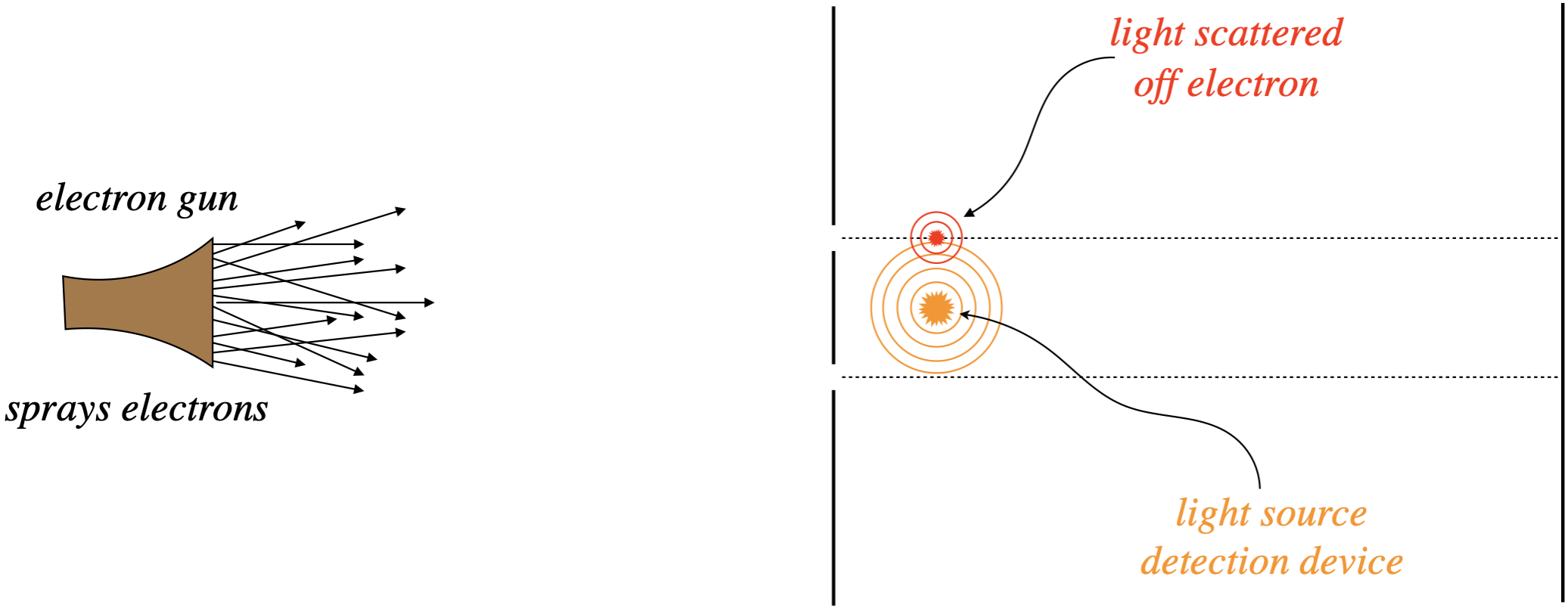
When we do this, we find we have a problem.  The interference pattern disappears, and the previous “expected” pattern of electrons landing either opposite one slit or the other emerges.  Apparently we have affected the motion of the electrons after they pass through the slit with our detection device.  But of course we have!  Light has momentum, and when we scatter it off the electrons, the momenta of the electrons are altered, apparently ruining the interference effect we were trying to study.  So the obvious solution?  Use light with less momentum, so that it doesn’t transfer so much to the electrons.  The means we have to use light of long wavelengths.

We previously discussed the limits on resolution of an observation based on the wavelength of light used to make that observation. We noted that wavelengths longer than the slit separation of a double slit will not be able to provide information about the slit separation. Well it turns out that in order to stop affecting the motions of the electrons by using longer-wavelength light, the wavelength must be longer than the space between the slits. So we can use light that doesn't transfer enough momentum to significantly affect the trajectories of the electrons (keeping the interference pattern), but in doing so, the loss of resolution for that longer wavelength makes it impossible for us to determine which slit the electron goes through, which was our whole reason for introducing the light in the first place!  Infuriating... and amazing.

Quantum States

One thing this result tells us is that our classical notion of predicting the exact motion of particles using Newton's laws and kinematics must be discarded. Trajectories of particles are inherently probabilistic, and yet there is nevertheless a certain degree of predictability – the interference pattern is quite repeatable. So our task in studying this subject is to determine what physical properties contribute to the observed behavior, and come up with a mathematical model to predict – in a probabilistic manner – the results of experiments with these particles.

We already have an example of how we can use physical properties to predict this probabilistic behavior. The momentum of a particle is directly related to the associated wave's wavelength. So we can make a prediction of where no particles will land on the screen (dark fringes) by knowing how fast the particles were moving (and of course their masses) when we shot them at the double slit.

Given the weirdness of these quanta, it's not clear what all the properties are that define the probabilities we seek to predict. When we studied thermodynamics in Physics 9HB, we defined something we called a "thermodynamic state". This was the equilibrium condition of a system, which was completely defined by several variables, like temperature, pressure, and volume. We will now define what we call a quantum state. Unlike a thermodynamic state, where knowing enough thermodynamic quantities to define the state tells us the values of other quantities (e.g. knowing the number of moles, volume, and pressure of an idea gas tells us exactly its temperature), in quantum physics, we can usually only know probabilities of the state's values being measured.

If we are interested in the position of a particle, we sort the quantum state into a collection of probabilities for every point in space. We will simplify this discussion by restricting ourselves to a "space" on one dimension. The information that the quantum state holds about the probabilities of various positions is called the wave function. In the language of the bras and kets discussed in Section 1.6, the wave function is the "component" of the quantum state vector that multiplies the unit vector defining position \(x\):

\[\psi\left(x\right)=\left<x|\psi\right>\]

We have greatly simplified things here (for example, we have not made any mention of how the quantum state evolves through time), but the general idea is this: The wave function \(\psi\left(x\right)\)...

• ... carries information about the probability of the particle being measured ("making a dot") at position \(x\),
• ... obeys the superposition principle, which means it can interfere with itself to create things like double-slit patterns and standing waves,
• ... has wave properties like wavelength (or a combination of wavelengths, if it is a superposition of waves) that correspond to physical properties like momentum,
• ... depends upon the physical situation that the particle finds itself in (like being acted-upon by external forces)

The topic of quantum mechanics is the study of solving for this wave function in various situations, and using it to make probabilistic predictions of what will be observed.