1.1: Measurement Error
( \newcommand{\kernel}{\mathrm{null}\,}\)
The result of a single measurement should be reported in the format (estimate)±(measurement error).
- The measurement error has one significant figure.
- The estimate has the same precision as the measurement error.
Suppose you use a digital multimeter to measure the current in a circuit, and the readout is stable (i.e., not fluctuating). Then you should report a result like this:
 =(0.320±0.005)A
=(0.320±0.005)A
Why? According to the readout, the value is between 0.315A (rounded up to 0.32A) and 0.324999…A (which is rounded down). So the measurement error is ±0.005A. Note that the estimate is reported as 0.320A to have the same precision as the error.
When using a device with hatch marks, such as a ruler or analog oscilloscope display, the measurement error is determined by the smallest markings. For example, if the smallest markings on a ruler have 1mm spacing, the measurement error is ±0.5mm, so a reading should be reported like this:
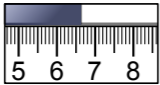 =(6.60±0.05)cm
=(6.60±0.05)cm
In more complicated situations, you must exercise your judgment. For instance, suppose you have a digital multimeter reading that is not stable: the last digit changes constantly, so that the reading fluctuates between 0.32, 0.33, and 0.34A. The value is between 0.315A and 0.344999…A, which is a range of ±0.015A. Since we use one significant figure for errors, the result is reported like this:
 =(0.33±0.02)A
=(0.33±0.02)A
Alternatively, suppose the last digit is changing so fast that you can’t make out its values at all. Then you can report the result like this:
 =(0.35±0.05)A
=(0.35±0.05)A
Measurement uncertainties can also come from other aspects of an experiment. Suppose you use a ruler to measure the distance to an object, but the object wobbles by ±2mm, larger than the 1mm hatch marks of the ruler. In that case, you should report a measurement error of ±2mm, not ±0.05mm.


