1.34: Galilean Relativity
( \newcommand{\kernel}{\mathrm{null}\,}\)
 We now extend our discussion of spatial geometry to spacetime geometry. We begin with Galilean relativity, which we will then generalize in the next section to Einstein (or Lorentz) relativity.
We now extend our discussion of spatial geometry to spacetime geometry. We begin with Galilean relativity, which we will then generalize in the next section to Einstein (or Lorentz) relativity.
The notion of relativity of motion is not something new with Einstein. It's built into Newtonian mechanics as well. The idea is that the results of experiments done in any inertial frame will be the same; i.e., one will not be able to determine by some experimental means what frame is at "absolute rest" and which frames are moving -- all motion is relative. An inertial frame is one in which Newton's laws of motion are satisfied. These laws prescribe accelerations, not velocities, so a frame that is moving at constant relative velocity with respect to an inertial frame must itself be an inertial frame.
Let's begin by considering a labeling of all points in space, at all points in time, with t,x,y,z. Further, let's assume the spatial part of this is a Cartesian coordinate system such that a ruler (at rest in this coordinate systems) with one end at t,x,y,z and the other at t,x+dx,y+dy,z+dz has length whose square is dℓ2=dx2+dy2+dz2 and the time labeling is such that a clock that goes from t,x,y,z to t+dt,x,y,z will indicate that the time elapsed is dt. Further, we will assume that this reference frame is inertial: Newton's laws of motion are satisfied in this frame.
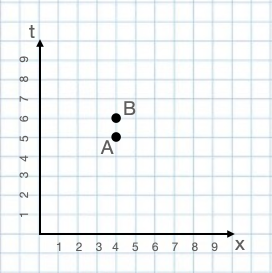
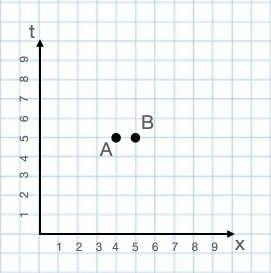
An example of such a coordinate system, although with just one spatial dimension, is shown in the first two figures in this chapter. A ruler stretching from point A to point B in the figure with these points horizontally displaced from each other, if the units of the tick marks on the x axis are in cm, would measure 1 cm. A clock that moves from A to B in the second figure, if the units on the t axis are seconds, would show a time elapsed of one second.
Now imagine a ball as it travels at uniform velocity from a spacetime point A to a spacetime point B. Let's set this up so that point A is t=2 seconds and x=4 cm and point B is at t=5 seconds and x=7 cm as in the figure to the left. From this given information we can conclude that the ball is moving toward increasing values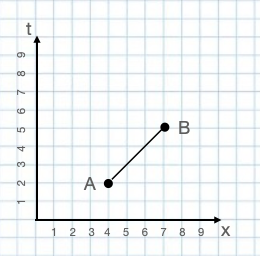 of x at constant speed v=1 cm/s. Let's define another reference frame, called the primed frame, which is coincident with the original unprimed frame at t=t′=0 but relative to the unprimed frame is moving to the right at speed v=1 cm/s just like the ball. In the primed frame (see the figure to the right) the origin of the primed frame is not moving (by definition), the ball is not moving, and the origin of the unprimed frame is moving toward decreasing values of x′ at speed v. The principle of relativity assures us that we can construct this primed frame so that it
of x at constant speed v=1 cm/s. Let's define another reference frame, called the primed frame, which is coincident with the original unprimed frame at t=t′=0 but relative to the unprimed frame is moving to the right at speed v=1 cm/s just like the ball. In the primed frame (see the figure to the right) the origin of the primed frame is not moving (by definition), the ball is not moving, and the origin of the unprimed frame is moving toward decreasing values of x′ at speed v. The principle of relativity assures us that we can construct this primed frame so that it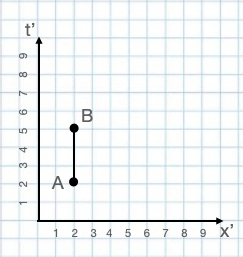 also has the same nice properties of the unprimed frame; i.e., the Pythagorean theorem applies for lengths, and the readings of stationary clocks make sense; i.e., a clock that goes from t′,x′,y′,z′ to t′+dt′,x′,y′,z′ will indicate that the time elapsed is dt′. The principle of relativity also leads us to the conclusion that if the unprimed frame is an inertial frame, the primed frame will be as well.
also has the same nice properties of the unprimed frame; i.e., the Pythagorean theorem applies for lengths, and the readings of stationary clocks make sense; i.e., a clock that goes from t′,x′,y′,z′ to t′+dt′,x′,y′,z′ will indicate that the time elapsed is dt′. The principle of relativity also leads us to the conclusion that if the unprimed frame is an inertial frame, the primed frame will be as well.
So far we have not mentioned Galileo. The above statements all follow from the principle of relativity, and our assumption that space is Euclidean. We specialize to Galilean relativity when we assume that the relationship between these two coordinate systems is:
t′=t,x′=x−vt,y′=y, andz′=z
Because the relationship is time dependent (and because we are anticipating the generalization to Lorentz transformations), we have explicitly included time in the transformation, even though time transforms trivially. We will call such a transformation a "Galilean Boost." In this case the above equations describe the relationship between a reference frame we denote without primes (the unprimed reference frame) and a reference frame that we denote with primes (the primed reference frame), where the primed reference frame is moving relative to the unprimed reference frame with speed v in the +x direction.
One can quickly verify that, if evaluated at the same time t, the distance between two infinitesimally separated points is unchanged by this transformation. Further, the transformation is symmetric. That is, there is nothing special about the primed frame relative to the unprimed frame. The reverse transformation, found by solving the above for t, x, y, and z is
t=t′,x=x′+vt′,y=y′, andz=z′
which is the same equation as above except with the replacement of v with −v. That is, it is exactly the same rule, with v→−v because while the primed frame is moving relative to the unprimed frame toward higher x, the unprimed frame is moving relative to the primed frame toward lower x′.
Box 1.34.1
Exercise 3.1.1: With the Galilean boost transformation, velocities add in a simple manner. If u′=dx′/dt′ where x′(t′) is the x′ location of some particle at time t′, find u=dx/dt as a function of u′ and v.
Box 1.34.2
Exercise 3.2.1: Show that Newton's Law for a spring is invariant under a Galilean transformation. In particular, show that the equation m¨x=−k(x−xc) is invariant under a Galilean transformation assuming the location of the force-free point of the spring, xc, is transformed as well. Here we have taken the spring equilibrium length to be zero and the spring constant to be k.
Box 1.34.3
Exercise 3.3.1: Discuss what this invariance means for applicability of Newton's laws in both the primed and unprimed frames, and the question: "is such a law consistent with the principal of Galilean relativity?"


