1.9: A Newtonian Homogeneous Expanding Universe
( \newcommand{\kernel}{\mathrm{null}\,}\)
Let's consider a homogeneous and isotropic expanding universe in a Newtonian manner: space is fixed, and the universe is filled with a fluid that is moving in such a manner as to keep the density spatially uniform. Is such a fluid flow possible? We are going to begin by assuming the fluid is undergoing a uniform expansion so we have distances between all pairs of fluid elements scaling up over time with some scale factor a(t). We will show that the fluid flow resulting from such an assumption is consistent with both the maintenance of uniform density over time and the conservation of mass. So such a flow is indeed kinematically possible. In the next section we will study the dynamics of this flow under the influence of gravity.
With uniform expansion we can write the location of all fluid elements as evolving over time as
→x(t)=a(t)→xc
where →xc is some fixed quantity for each fluid element. The 'c' stands for comoving. We consider any fluid element following this rule to be 'comoving' with the expansion; i.e., its only motion is due to the expansion. In our completely homogeneous universe, all fluid elements are 'comoving' in this way.
The velocity of any fluid element is then
→v=d→x/dt=˙a→xc=(˙a/a)→x
and, as expected for uniform expansion, we see we have Hubble's law (or rather a vector version of it).
Does this pattern of fluid flow preserve homogeneity? Let's see by looking at the continuity equation, which follows from mass conservation:
∂ρ/∂t=−→∇⋅(ρ→v).
If we assume ρ is initially uniform then the right-hand side can be written as - ρ→∇⋅→v. Substituting in the expression for the velocity field in Equation ??? one can show (see the Exercise) that →∇⋅→v=3˙a/a. By assumption, ˙a/a is independent of location so the continuity equation says that if the field is initially homogeneous, its time derivative is independent of location so it will stay homogeneous. So we have demonstrated what we wanted to demonstrate: the uniform expansion represented by Equation ??? leads to a fluid flow that indeed preserves homogeneity.
Box 1.9.1
Exercise 10.1.1: Show that if →x(t)=a(t)→xc that →v=d→x(t)/dt∝→x. Find the proportionality constant in terms of a(t) and its time derivative (where by constant here we mean the same everywhere, not necessarily constant in time). Then show that →∇⋅→v=3˙a/a.
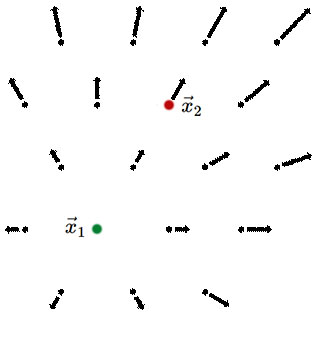
Hubble's law, as seen in the above exercise, does not look homogeneous. After all, there's a special point that has zero velocity. But this is just a matter of the choice of coordinate system and is not a real inhomogeneity. We'll explicitly demonstrate now that Hubble's law is valid even if you chose a different point to be the one at rest. If the point at rest is →x1, then any point →x, has velocity →v=(→x−→x1)˙a/a. We'll call this the vector version of Hubble's Law. An observer at rest with respect to the fluid at →x1 will see a flow as shown in the left panel of the figure below.
 |
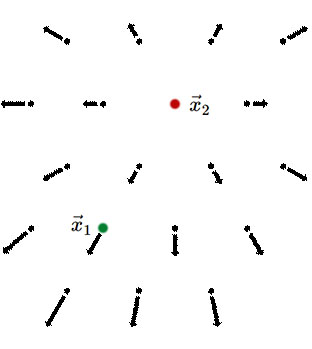 |
| Coordinate system with →x1 as the point at rest and seeming center of expansion. Image by Bryan Miller. | Coordinate system with →x2 as the point at rest. Image by Bryan Miller. |
What will an observer at rest with respect to the fluid at location x2 see? In our original unprimed coordinate system we have
→v2=(→x2−→x1)˙a/a(unprimedsystem)
and we want →v′2=0 via a Galilean transformation to the unprimed system, so we subtract →v2 from the unprimed velocities everywhere:
→v′=→v−→v2(Galilean velocity transformationrule)=(→x−→x1)˙a/a−(→x2−→x1)˙a/a=(→x−→x2)˙a/a
So we see that we still have Hubble's Law. We see that arranging the fluid so that it all flows away from a given point with speed linearly dependent on distance preserves homogeneity and isotropy.
Although we first derived Hubble's Law in the context of a relativistic description of spacetime, we now see it arising in a Newtonian context. Fundamentally, Hubble's Law follows from the uniformity of the expansion, whether that's a fluid that's expanding or space itself.
HOMEWORK Problems
Problem 1.9.1
Demonstrate that a universe obeying a nonlinear version of Hubble's law would violate homogeneity. Take v=H0d2 for specificity and work in one dimension for simplicity. Show that assuming this velocity pattern about one point leads to a different velocity pattern around other points, thereby demonstrating the violation of homogeneity. You can do this by thinking of 3 points all in one line, with the central point the same distance from the surrounding two.


