11.7: The Big Bang
- Page ID
- 4560
By the end of this section, you will be able to:
- Explain the expansion of the universe in terms of a Hubble graph and cosmological redshift
- Describe the analogy between cosmological expansion and an expanding balloon
- Use Hubble’s law to make predictions about the measured speed of distant galaxies
We have been discussing elementary particles, which are some of the smallest things we can study. Now we are going to examine what we know about the universe, which is the biggest thing we can study. The link between these two topics is high energy: The study of particle interactions requires very high energies, and the highest energies we know about existed during the early evolution of the universe. Some physicists think that the unified force theories we described in the preceding section may actually have governed the behavior of the universe in its earliest moments.
Hubble’s Law
In 1929, Edwin Hubble published one of the most important discoveries in modern astronomy. Hubble discovered that
- galaxies appear to move away from Earth and
- the velocity of recession (\(v\)) is proportional to the distance (\(d\)) of the galaxy from Earth.
Both \(v\) and \(d\) can be determined using stellar light spectra. A best fit to the sample illustrative data is given in Figure \(\PageIndex{1}\). (Hubble’s original plot had a considerable scatter but a general trend was still evident.)
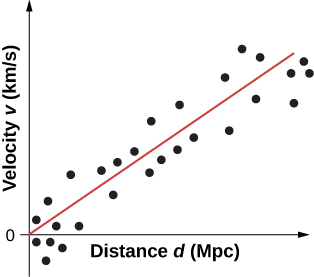
The trend in the data suggests the simple proportional relationship:
\[v = H_0d, \nonumber \]
where \(H_0 = 70 \, km /s /Mpc\) is known as Hubble’s constant. (Note: 1 Mpc is one megaparsec or one million parsecs, where one parsec is 3.26 light-years.) This relationship, called Hubble’s law, states that distant stars and galaxies recede away from us at a speed of 70 km/s for every one megaparsec of distance from us. Hubble’s constant corresponds to the slope of the line in Figure \(\PageIndex{1}\). Hubble’s constant is a bit of a misnomer, because it varies with time. The value given here is only its value today.
Watch this video to learn more about the history of Hubble’s constant.
The rate at which the universe is expanding, a value known as the Hubble constant, has been hotly debated for the last 80 years. Now the director of the Carnegie Observatories, Wendy Freedman, will lead a team who will slash the uncertainty of this value to just 3% via the new Carnegie Hubble Program using NASAs space-based Spitzer telescope.
Hubble’s law describes an average behavior of all but the closest galaxies. For example, a galaxy 100 Mpc away (as determined by its size and brightness) typically moves away from us at a speed of
\[v = \left( \left( 70 \frac{km}{s}\right)/Mpc \right) (100 \, Mpc) = 7000 \, km/s. \nonumber \]
This speed may vary due to interactions with neighboring galaxies. Conversely, if a galaxy is found to be moving away from us at speed of 100,000 km/s based on its red shift, it is at a distance
\[d = v/H_0 = (10,000 \, km/s)/ \left( \left( 70 \frac{km}{s}\right) /Mpc \right) = 143 \, Mpc. \nonumber \]
This last calculation is approximate because it assumes the expansion rate was the same 5 billion years ago as it is now.
Big Bang Model
Scientists who study the origin, evolution, and ultimate fate of the universe (cosmology) believe that the universe began in an explosion, called the Big Bang, approximately 13.7 billion years ago. This explosion was not an explosion of particles through space, like fireworks, but a rapid expansion of space itself. The distances and velocities of the outward-going stars and galaxies permit us to estimate when all matter in the universe was once together—at the beginning of time.
Scientists often explain the Big Bang expansion using an inflated-balloon model (Figure \(\PageIndex{2}\)). Dots marked on the surface of the balloon represent galaxies, and the balloon skin represents four-dimensional space-time. As the balloon is inflated, every dot “sees” the other dots moving away. This model yields two insights. First, the expansion is observed by all observers in the universe, no matter where they are located. The “center of expansion” does not exist, so Earth does not reside at the “privileged” center of the expansion.
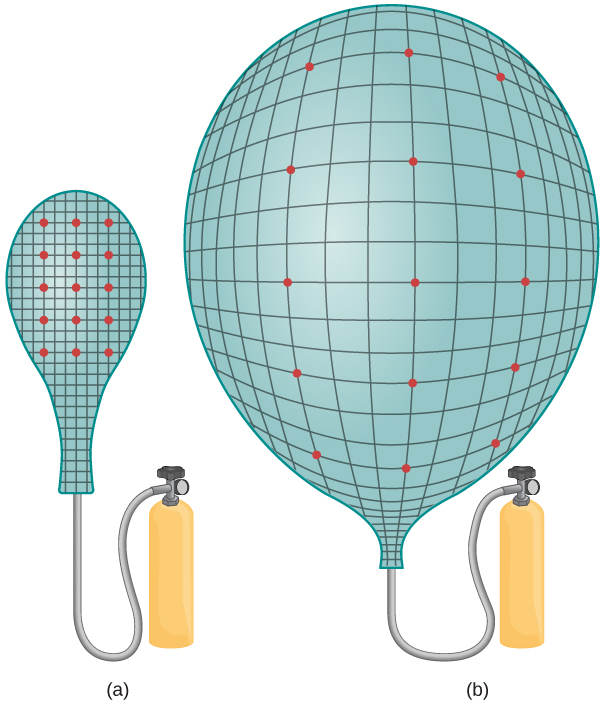
Second, as mentioned already, the Big Bang expansion is due to the expansion of space, not the increased separation of galaxies in ordinary (static) three-dimensional space. This cosmological expansion affects all things: dust, stars, planets, and even light. Thus, the wavelength of light (\(\lambda\))emitted by distant galaxies is “stretched” out. This makes the light appear “redder” (lower energy) to the observer—a phenomenon called cosmological redshift. Cosmological redshift is measurable only for galaxies farther away than 50 million light-years.
A galaxy is observed to have a redshift:
\[z = \frac{\lambda_{obs} - \lambda_{emit}}{\lambda_{emit}} = 4.5. \nonumber \]
This value indicates a galaxy moving close to the speed of light. Using the relativistic redshift formula (given in Relativity), determine:
- How fast is the galaxy receding with respect to Earth?
- How far away is the galaxy?
Strategy
We need to use the relativistic Doppler formula to determine speed from redshift and then use Hubble’s law to find the distance from the speed.
Solution
- According to the relativistic redshift formula: \[z = \sqrt{\frac{1 + \beta}{1 - \beta}} - 1, \nonumber \] where \(\beta = v/c\). Substituting the value for z and solving for \(\beta\), we get \(\beta = 0.93\). This value implies that the speed of the galaxy is \(2.8 \times 10^8 \, m/s\).
- Using Hubble’s law, we can find the distance to the galaxy if we know its recession velocity: \[d = \frac{v}{H_0} = \frac{2.8 \times 10^8 \, m/s}{73.8 \times 10^3 \, m/s \, per \, Mpc} = 3.8 \times 10^3 \, Mpc. \nonumber \]
Significance
Distant galaxies appear to move very rapidly away from Earth. The redshift of starlight from these galaxies can be used to determine the precise speed of recession, over \(90%\) of the speed of light in this case. This motion is not due to the motion of galaxy through space but by the expansion of space itself.
The light of a galaxy that moves away from us is “redshifted.” What occurs to the light of a galaxy that moves toward us?
- Answer
-
blueshifted
View this video to learn more about the cosmological expansion.
The Expanding Universe.
Structure and Dynamics of the Universe
At large scales, the universe is believed to be both isotropic and homogeneous. The universe is believed to isotropic because it appears to be the same in all directions, and homogeneous because it appears to be the same in all places. A universe that is isotropic and homogeneous is said to be smooth. The assumption of a smooth universe is supported by the Automated Plate Measurement Galaxy Survey conducted in the 1980s and 1900s (Figure \(\PageIndex{3}\)). However, even before these data were collected, the assumption of a smooth universe was used by theorists to simplify models of the expansion of the universe. This assumption of a smooth universe is sometimes called the cosmological principle.

The fate of this expanding and smooth universe is an open question. According to the general theory of relativity, an important way to characterize the state of the universe is through the space-time metric:
\[ds^2 = c^2dt^2 - a(t)^2 d\Sigma^2, \nonumber \]
where c is the speed of light, a is a scale factor (a function of time), and \(d\Sigma\) is the length element of the space. In spherical coordinates \((r, \theta, \phi)\), this length element can be written
\[d\Sigma^2 = \frac{dr^2}{1 - kr^2} + r^2(d\theta^2 + sin^2 \theta d\varphi^2), \nonumber \]
where k is a constant with units of inverse area that describes the curvature of space. This constant distinguishes between open, closed, and flat universes:
- \(k = 0\) (flat universe)
- \(k > 0\) (closed universe, such as a sphere)
- \(k < 0\) (open universe, such as a hyperbola)
In terms of the scale factor a, this metric also distinguishes between static, expanding, and shrinking universes:
- \(a = 1\) (static universe)
- \(da/dt > 0\) (expanding universe)
- \(da/dt < 0\) (shrinking universe)
The scale factor a and the curvature k are determined from Einstein’s general theory of relativity. If we treat the universe as a gas of galaxies of density \(\rho\) and pressure p, and assume \(k = 0\) (a flat universe), than the scale factor a is given by
\[\frac{d^2a}{dt^2} = - \frac{4\pi G}{3} (\rho + 3p) a, \nonumber \]
where G is the universal gravitational constant. (For ordinary matter, we expect the quantity \(\rho + 3p\) to be greater than zero.) If the scale factor is positive \((a > 0)\), the value of the scale factor “decelerates” \((d^2a/dt^2 < 0)\), and the expansion of the universe slows down over time. If the numerator is less than zero (somehow, the pressure of the universe is negative), the value of the scale factor “accelerates,” and the expansion of the universe speeds up over time. According to recent cosmological data, the universe appears to be expanding. Many scientists explain the current state of the universe in terms of a very rapid expansion in the early universe. This expansion is called inflation.


