6.5: Magnetic Field Near a Long, Straight, Current-carrying Conductor
- Page ID
- 5449
Consider a point \(P\) at a distance \(a\) from a conductor carrying a current \(I\) (Figure VI.4).
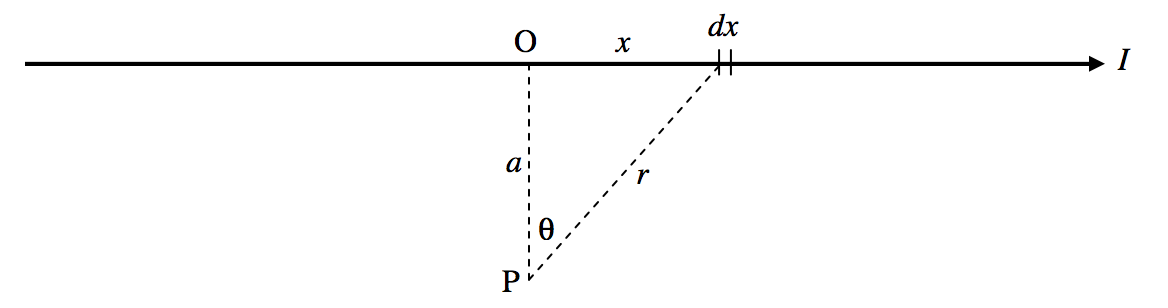
\(\text{FIGURE VI.4}\)
The contribution to the magnetic field at \(P\) from the elemental length \(dx\) is
\[dB = \frac{\mu}{4\pi}\cdot \frac{I\,dx \cos \theta }{r^2}.\label{6.5.1}\]
(Look at the way I have drawn \(\theta\) if you are worried about the cosine.)
Here I have omitted the subscript zero on the permeability to allow for the possibility that the wire is immersed in a medium in which the permeability is not the same as that of a vacuum. (The permeability of liquid oxygen, for example, is slightly greater than that of free space.) The direction of the field at \(P\) is into the plane of the “paper” (or of your computer screen).
We need to express this in terms of one variable, and we’ll choose \(\theta\). We can see that \(r=a\sec \theta\) and \(x=a\tan \theta\) so that \(dx=a\sec^2 \theta \, d\theta\). Thus Equation \ref{6.5.1} becomes
\[dB=\frac{\mu I}{4\pi a}\sin \theta \, d\theta .\]
Upon integrating this from \(-\pi/2 \text{ to }+ \pi/2\) (or from \(0\text{ to }\pi/2\) and then double it), we find that the field at \(P\) is
\[B=\frac{\mu I}{2\pi a}.\]
Note the \(2\pi\) in this problem with cylindrical symmetry.


