3.7: Angular Momentum
( \newcommand{\kernel}{\mathrm{null}\,}\)
Notation:
- LC= angular momentum of system with respect to centre of mass C.
- L = angular momentum of system relative to some other origin O.
- ¯r = position vector of C with respect to O.
- P = linear momentum of system with respect to O.
- (The linear momentum with respect to C is, of course, zero.)
L=LC+¯r×P
Thus:
L=∑ri×pi=∑mi(ri×vi)=∑mi(¯r+r′i)×(¯v+v′i)=(¯rׯv)∑mi+¯r×∑miv′i+(∑mir′i)ׯv+∑r′i×p′i=M(¯rׯv)+¯r×0+0ׯv+LC
therefore
L=LC+¯r×P
A hoop of radius a rolling along the ground (Figure III.6):
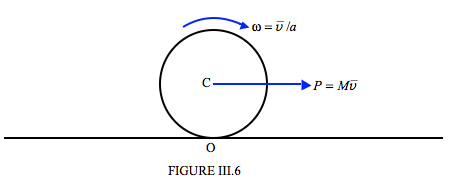
The angular momentum with respect to C is LC = ICω where IC is the rotational inertia about C. The angular momentum about O is therefore
I=ICω+M¯va=ICω+Ma2ω=(IC+Ma2)=Iω
where
I=IC+Ma2
is the rotational inertia about O.


