10.1: Relativity Requires Magnetism

Last updated
Save as PDF

Page ID: 3480

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Explain the following laws within the Ideal Gas Law

Relativity requires magnetism

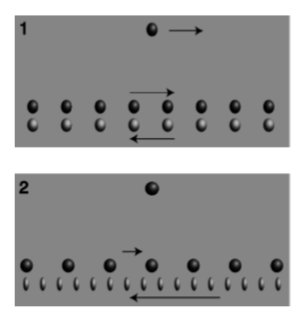
fig 10.1.1.png — Figure \(\PageIndex{1}\): A model of a charged particle and a current-carrying wire, seen in two different frames of reference. The relativistic length contraction is highly exaggerated. The force on the lone particle is purely magnetic in 1, and purely electric in 2.

Figure \(\PageIndex{1}\) is an unrealistic model of charged particle moving parallel to a current-carrying wire. What electrical force does the lone particle in figure \(\PageIndex{1}\) (1) feel? Since the density of "traffic'' on the two sides of the "road" is equal, there is zero overall electrical force on the lone particle. Each "car" that attracts the lone particle is paired with a partner on the other side of the road that repels it. If we didn’t know about magnetism, we’d think this was the whole story: the lone particle feels no force at all from the wire.

Figure \(\PageIndex{1}\) (2) shows what we’d see if we were observing all this from a frame of reference moving along with the lone charge. Relativity tells us that moving objects appear contracted to an observer who is not moving along with them. Both lines of charge are in motion in both frames of reference, but in frame \(1\) they were moving at equal speeds, so their contractions were equal. In frame \(2\), however, their speeds are unequal. The dark charges are moving more slowly than in frame \(1\), so in frame \(2\) they are less contracted. The light-colored charges are moving more quickly, so their contraction is greater now. The "cars'' on the two sides of the "road’’ are no longer paired off, so the electrical forces on the lone particle no longer cancel out as they did in \(\PageIndex{1}\) (1). The lone particle is attracted to the wire, because the particles attracting it are more dense than the ones repelling it.

Now observers in frames \(1\) and \(2\) disagree about many things, but they do agree on concrete events. Observer \(2\) is going to see the lone particle drift toward the wire due to the wire’s electrical attraction, gradually speeding up, and eventually hit the wire. If \(2\) sees this collision, then \(1\) must as well. But \(1\) knows that the total electrical force on the lone particle is exactly zero. There must be some new type of force. She invents a name for it: magnetism.

Magnetism is a purely relativistic effect. Since relativistic effects are down by a factor of \(v^2\) compared to Newtonian ones, it’s surprising that relativity can produce an effect as vigorous as the attraction between a magnet and your refrigerator. The explanation is that although matter is electrically neutral, the cancellation of electrical forces between macroscopic objects is extremely delicate, so anything that throws off the cancellation, even slightly, leads to a surprisingly large force.