Mass-Energy Equivalence
( \newcommand{\kernel}{\mathrm{null}\,}\)
Introduction
In this little document we justify Einstein's famous equation E = mc2. Sections 1 and 2 demonstrate how the relativistic mass increase arises. They are essentially non-mathematical and only require the following background information:
- According to the Special Theory of Relativity velocities do not add in the simple way that our "common sense" says.
- The Principle of Inertia, also known as Conservation of Momentum, is true for all collisions.
Sections 3 and 4 extend the discussion. They use only descriptive mathematics, but are non-trivial. Required background is knowing that:
- In the worldview of Special Relativity spacetime has four dimensions.
- The time squared minus the distance squared is the same number for all observers.
Finally, Section 5 revisits the sticky collisions of the Sections 1 and 2.
Non-relativistic Sticky Collisions
In this section we discuss non-relativistic collisions and the Principle of Inertia. Since the discussion is non-relativistic the results should conform to our "common sense" about what should happen.
To the right we show two objects approaching each other at 60 km/hr relative to us. We shall assume that the two objects have equal masses and are constructed of a "sticky" material.

When they two objects collide they stick together. Since before the collision the two objects had equal masses and were moving in opposite directions at the same speeds, their inertia or momenta were equal and opposite. Thus after the collision they will be stationary relative to us. This is an example of the Principle of Inertia, also called Conservation of Momentum.
![]()
Now we imagine looking at the same collision for the reference frame of an observer moving to the left at 60 km/hr relative to the first one. The right hand (red) ball will be stationary for this person, but the left hand (blue) ball will be moving at 60 + 60 = 120 km/hr.
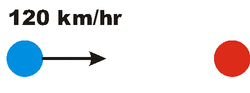
After the collision, the two balls stick together. Since the two balls that are stuck together have twice the mass of the left-hand (blue) ball by itself, after the collision the speed of the two must be one-half of 120 km/hr, i.e. 60 km/hr. Since for the first observer the two balls are stationary after the collision and the second observer is moving to the left at 60 km/hr, we can predict that after the collision the two balls will be moving at 60 km/hr relative to the second observer. So we have two ways of getting the result shown to the right: from Conservation of Momentum or from Galilean relativity.

Relativistic Sticky Collisions
Now we do a similar analysis, but this time the balls are moving at relativistic speeds. Their speeds are 60% of the speed of light relative to the shown observer Sue. We should emphasise that relative to Sue the balls have the same mass and are moving at the same speeds in opposite directions.
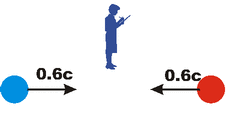
Thus, after the collision the Principle of Inertia says that the balls will be stationary relative to Sue.

Now we imagine an observer Lou who is moving to the left at 60% of the speed of light relative to Sue. The right-hand (red) ball will be stationary relative to Lou. The left-hand (blue) ball will be moving to the right relative to him. But because these are relativistic speeds, the left-hand ball will be moving at a speed less than 0.6c + 0.6c = 1.2c. It turns out that the speed of the left-hand ball is 0.88c.
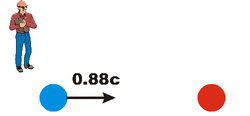
Now we have a problem. The Principle of Inertia predicts that after the collision the speed of the balls will be one-half of 0.88c, i.e. 0.44c. But if the balls were stationary relative to Sue after the collision and Lou is moving to the left at 0.6c relative to Sue, then surely the balls must be moving to the right at 0.6c relative to Lou. So Conservation of Momentum and Galilean relativity predict different results.

When Einstein was confronted with this, he refused to throw out the Principle of Inertia. Therefore, he concluded that before the collision, relative to Lou the mass of the left-hand (blue) ball must be greater than the mass of the right-hand (red) ball. Thus when an object is moving relative to some observer its mass increases as the speed increases. So the last figure above is correct.
You may wish to know that Einstein's analysis leading him to the relativistic mass increase was more complex than the above. Instead of considering the interaction of 2 massive objects he was thinking about the interaction between an electromagnetic field and a massive charged particle. This is a more difficult problem but the basic idea is the same.
It turns out that the relation between the mass m the body has when it is moving at speed v relative to an observer is related to the mass m0 it has relative to an observer for whom the body is at rest is given by the equation shown to the right. The quantity m0 is called the rest mass of the body. For Lou, before the collision the mass of the left-hand (blue) ball is greater than its rest mass by a factor of 2.11.
m=m0√1−v2/c2
Energy
Energy is a concept that has undergone continuous revision since the days of Newton. Originally it referred to a property that bodies have because they are in motion; today that property is called the kinetic energy. Other forms of energy have been discovered since then, with names like potential energy, heat energy, etc. Notice that the kinetic energy is another property, like inertia or momentum, that bodies have because of their motion.
Einstein realized that the fact that masses increase when they are moving relative to us means that the kinetic energy of a body could be related to this increase in mass. So the kinetic energy of a body is somehow related to the increase in mass:
kinetic energy ~ m - m0
However, the units of this are wrong. Energy units are a mass times a speed squared. In everyday units, this is a kg times a meter per second squared, which we call a joule. Above we say the energy goes only as the mass.
Relativity taught us that we made a mistake when we measured time in "sacred" units of seconds instead of everyday units of meters. And we learned that we can use the speed of light c as a conversion factor for units. We can apply that realization to the above to multiply the masses to the speed of light squared to get the units to come out right:
kinetic energy = (m - m0) c2
Einstein showed in 1905 that the above gives the Newtonian form for kinetic energy when the speed of the object v is small compared to the speed of light c.
Now, when the object is at rest relative to an observer, it has no kinetic energy. However what are we to make of the left-over term:
m0 c2
Einstein realized that this is yet another form of energy, a form that arises because of the body's rest mass. And the total energy of a body that is moving is this "rest energy" plus its kinetic energy. So:
Energy E = m0 c2 + (m - m0) c2 = m c2
As you probably know, there are other forms of energy than just the rest energy and the kinetic energy. There is heat energy, chemical energy, binding energies of atoms and nuclei, etc. etc. It turns out that all forms of energy are reflected in the total mass of the body. So although we have justified E = mc2 in terms of the kinetic energy, mass-energy equivalence is quite a bit more general.
Dimensionality of Spacetime
You will recall that in the worldview of Special Relativity, spacetime has four dimensions, the three spatial dimensions and the time dimension. Here we explore the consequences of this for energy. We shall be slightly mathematical, and will "push the envelope" a bit in terms of sophistication.
Now, the inertia or momentum of a body is related to its mass and its speed. But there is a bit more information than just this. The momentum of an object traveling, say, North is different than the momentum of an object traveling East or an object traveling up. So the momentum has three components, corresponding to the three spatial dimensions. By convention the momentum is given the symbol p, so the three components can be specified as px, py and pz
But spacetime has four dimensions. What can be the fourth time component of the momentum? A natural candidate is the other quantity that an object has related to its motion, its energy. So it is natural to say the the energy is the fourth component of the momentum.
The dimensions here don't quite work out. Momentum is a mass times a speed, while energy is a mass times a speed squared. But we can once again fix up the units using c. Multiply the spatial momenta by c and they will have the same units as the energy.
So to describe the position of an event occurring in spacetime we specify the four coordinates:
position = ct, x, y, z
To describe the relativistic momentum of an object we similarly specify its four components:
momentum = E, cpx, cpy, cpz
Finally, earlier we saw that although for different observers the time and position of some event may be different, there is a constant for all observers:
(ct)2 - x2 - y2 - z2
Similarly, although the momentum and energy of an object is different for different observers, there is a constant here too, the time component squared minus the spatial components squared:
E2 - (cpx)2 - (cpy)2 - (cpz)2
What can the value of this quantity be? We could go through all the math, but there is an easier approach. When the object is at rest with respect to us, it has no spatial momentum and its energy is just the rest energy. And if this is the value for an observer at rest relative to the object, then it must be the value for all observers.
E2 - (cpx)2 - (cpy)2 - (cpz)2 = (m0 c2) 2
In words, the value of the relativistic momentum squared is the rest mass squared.
Sticky Collisions Revisited
In the sticky collisions, initially the objects are moving and thus have kinetic energy. Relative to the observer for whom the objects are stationary after the collision, the objects have no kinetic energy after the collision. All the kinetic energy has been converted into heat energy. Relative to other observers, the kinetic energy after the collision is not zero, but is still less than the total kinetic energy before the collision: in this case the difference has also been converted to heat.
But according to E = mc2, energy and mass are equivalent. Thus the heat energy H generated in the collision will have a mass mheat = H/c2. This is a real mass and has inertia. It turns out that if one tries to apply Conservation of Momentum to the collisions, this additional mass and its momentum must be accounted for in the equations.
A discussion of this plus a recap of Sections 1 and 2 of this document, written for physicists, is available in pdf format here. File size is 66k and it will appear in a separate window.

