3.E: Interference (Exercises)
- Page ID
- 7855
Conceptual Questions
3.1 Young's Double-Slit Interference
1. Young’s double-slit experiment breaks a single light beam into two sources. Would the same pattern be obtained for two independent sources of light, such as the headlights of a distant car? Explain.
2. Is it possible to create a experimental setup in which there is only destructive interference? Explain.
3. Why won’t two small sodium lamps, held close together, produce an interference pattern on a distant screen? What if the sodium lamps were replaced by two laser pointers held close together?
3.2 Mathematics of Interference
4. Suppose you use the same double slit to perform Young’s double-slit experiment in air and then repeat the experiment in water. Do the angles to the same parts of the interference pattern get larger or smaller? Does the color of the light change? Explain.
5. Why is monochromatic light used in the double slit experiment? What would happen if white light were used?
3.4 Interference in Thin Films
6. What effect does increasing the wedge angle have on the spacing of interference fringes? If the wedge angle is too large, fringes are not observed. Why?
7. How is the difference in paths taken by two originally in-phase light waves related to whether they interfere constructively or destructively? How can this be affected by reflection? By refraction?
8. Is there a phase change in the light reflected from either surface of a contact lens floating on a person’s tear layer? The index of refraction of the lens is about 1.5, and its top surface is dry.
9. In placing a sample on a microscope slide, a glass cover is placed over a water drop on the glass slide. Light incident from above can reflect from the top and bottom of the glass cover and from the glass slide below the water drop. At which surfaces will there be a phase change in the reflected light?
10. Answer the above question if the fluid between the two pieces of crown glass is carbon disulfide.
11. While contemplating the food value of a slice of ham, you notice a rainbow of color reflected from its moist surface. Explain its origin.
12. An inventor notices that a soap bubble is dark at its thinnest and realizes that destructive interference is taking place for all wavelengths. How could she use this knowledge to make a nonreflective coating for lenses that is effective at all wavelengths? That is, what limits would there be on the index of refraction and thickness of the coating? How might this be impractical?
13. A nonreflective coating like the one described in Example 3.3 works ideally for a single wavelength and for perpendicular incidence. What happens for other wavelengths and other incident directions? Be specific.
14. Why is it much more difficult to see interference fringes for light reflected from a thick piece of glass than from a thin film? Would it be easier if monochromatic light were used?
3.5 The Michelson Interferometer
15. Describe how a Michelson interferometer can be used to measure the index of refraction of a gas (including air).
Problems
3.2 Mathematics of Interference
16. At what angle is the first-order maximum for 450-nm wavelength blue light falling on double slits separated by 0.0500 mm?
17. Calculate the angle for the third-order maximum of 580-nm wavelength yellow light falling on double slits separated by 0.100 mm.
18. What is the separation between two slits for which 610-nm orange light has its first maximum at an angle of \(\displaystyle 30.0°\)?
19. Find the distance between two slits that produces the first minimum for 410-nm violet light at an angle of \(\displaystyle 45.0°\).
20. Calculate the wavelength of light that has its third minimum at an angle of \(\displaystyle 30.0°\) when falling on double slits separated by \(\displaystyle 3.00μm\). Explicitly show how you follow the steps from the Problem-Solving Strategy: Wave Optics, located at the end of the chapter.
21. What is the wavelength of light falling on double slits separated by \(\displaystyle 2.00μm\) if the third-order maximum is at an angle of \(\displaystyle 60.0°\)?
22. At what angle is the fourth-order maximum for the situation in the preceding problem?
23. What is the highest-order maximum for 400-nm light falling on double slits separated by \(\displaystyle 25.0μm\)?
24. Find the largest wavelength of light falling on double slits separated by \(\displaystyle 1.20μm\) for which there is a first-order maximum. Is this in the visible part of the spectrum?
25. What is the smallest separation between two slits that will produce a second-order maximum for 720-nm red light?
26. (a) What is the smallest separation between two slits that will produce a second-order maximum for any visible light?
(b) For all visible light?
27. (a) If the first-order maximum for monochromatic light falling on a double slit is at an angle of \(\displaystyle 10.0°\), at what angle is the second-order maximum?
(b) What is the angle of the first minimum?
(c) What is the highest-order maximum possible here?
28. Shown below is a double slit located a distance x from a screen, with the distance from the center of the screen given by y. When the distance d between the slits is relatively large, numerous bright spots appear, called fringes. Show that, for small angles (where \(\displaystyle sinθ≈θ\), with \(\displaystyle θ\) in radians), the distance between fringes is given by \(\displaystyle Δy=xλ/d\)
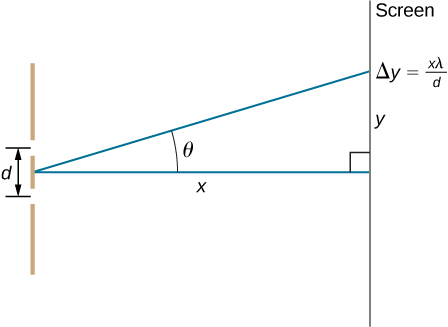
Picture shows a double slit located a distance x from a screen, with the distance from the center of the screen given by y. Distance between the slits is d.
29. Using the result of the preceding problem,
(a) calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen.
(b) What would be the distance between fringes if the entire apparatus were submersed in water, whose index of refraction is 1.33?
30. Using the result of the problem two problems prior, find the wavelength of light that produces fringes 7.50 mm apart on a screen 2.00 m from double slits separated by 0.120 mm.
31. In a double-slit experiment, the fifth maximum is 2.8 cm from the central maximum on a screen that is 1.5 m away from the slits. If the slits are 0.15 mm apart, what is the wavelength of the light being used?
32. The source in Young’s experiment emits at two wavelengths. On the viewing screen, the fourth maximum for one wavelength is located at the same spot as the fifth maximum for the other wavelength. What is the ratio of the two wavelengths?
33. If 500-nm and 650-nm light illuminates two slits that are separated by 0.50 mm, how far apart are the second-order maxima for these two wavelengths on a screen 2.0 m away?
34. Red light of wavelength of 700 nm falls on a double slit separated by 400 nm.
(a) At what angle is the first-order maximum in the diffraction pattern?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
3.3 Multiple-Slit Interference
35. Ten narrow slits are equally spaced 0.25 mm apart and illuminated with yellow light of wavelength 580 nm. (a) What are the angular positions of the third and fourth principal maxima? (b) What is the separation of these maxima on a screen 2.0 m from the slits?
36. The width of bright fringes can be calculated as the separation between the two adjacent dark fringes on either side. Find the angular widths of the third- and fourth-order bright fringes from the preceding problem.
37. For a three-slit interference pattern, find the ratio of the peak intensities of a secondary maximum to a principal maximum.
38. What is the angular width of the central fringe of the interference pattern of
(a) 20 slits separated by \(\displaystyle d=2.0×10^{−3}mm\)?
(b) 50 slits with the same separation? Assume that \(\displaystyle λ=600nm\).
3.4 Interference in Thin Films
39. A soap bubble is 100 nm thick and illuminated by white light incident perpendicular to its surface. What wavelength and color of visible light is most constructively reflected, assuming the same index of refraction as water?
40. An oil slick on water is 120 nm thick and illuminated by white light incident perpendicular to its surface. What color does the oil appear (what is the most constructively reflected wavelength), given its index of refraction is 1.40?
41. Calculate the minimum thickness of an oil slick on water that appears blue when illuminated by white light perpendicular to its surface. Take the blue wavelength to be 470 nm and the index of refraction of oil to be 1.40.
42. Find the minimum thickness of a soap bubble that appears red when illuminated by white light perpendicular to its surface. Take the wavelength to be 680 nm, and assume the same index of refraction as water.
43. A film of soapy water (\(\displaystyle n=1.33\)) on top of a plastic cutting board has a thickness of 233 nm. What color is most strongly reflected if it is illuminated perpendicular to its surface?
44. What are the three smallest non-zero thicknesses of soapy water (\(\displaystyle n=1.33\)) on Plexiglas if it appears green (constructively reflecting 520-nm light) when illuminated perpendicularly by white light?
45. Suppose you have a lens system that is to be used primarily for 700-nm red light. What is the second thinnest coating of fluorite (magnesium fluoride) that would be nonreflective for this wavelength?
46. (a) As a soap bubble thins it becomes dark, because the path length difference becomes small compared with the wavelength of light and there is a phase shift at the top surface. If it becomes dark when the path length difference is less than one-fourth the wavelength, what is the thickest the bubble can be and appear dark at all visible wavelengths? Assume the same index of refraction as water.
(b) Discuss the fragility of the film considering the thickness found.
47. To save money on making military aircraft invisible to radar, an inventor decides to coat them with a nonreflective material having an index of refraction of 1.20, which is between that of air and the surface of the plane. This, he reasons, should be much cheaper than designing Stealth bombers.
(a) What thickness should the coating be to inhibit the reflection of 4.00-cm wavelength radar?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
3.5 The Michelson Interferometer
48. A Michelson interferometer has two equal arms. A mercury light of wavelength 546 nm is used for the interferometer and stable fringes are found. One of the arms is moved by \(\displaystyle 1.5μm\). How many fringes will cross the observing field?
49. What is the distance moved by the traveling mirror of a Michelson interferometer that corresponds to 1500 fringes passing by a point of the observation screen? Assume that the interferometer is illuminated with a 606 nm spectral line of krypton-86.
50. When the traveling mirror of a Michelson interferometer is moved \(\displaystyle 2.40×10^{−5}m\), 90 fringes pass by a point on the observation screen. What is the wavelength of the light used?
51. In a Michelson interferometer, light of wavelength 632.8 nm from a He-Ne laser is used. When one of the mirrors is moved by a distance D, 8 fringes move past the field of view. What is the value of the distance D?
52. A chamber 5.0 cm long with flat, parallel windows at the ends is placed in one arm of a Michelson interferometer (see below). The light used has a wavelength of 500 nm in a vacuum. While all the air is being pumped out of the chamber, 29 fringes pass by a point on the observation screen. What is the refractive index of the air?
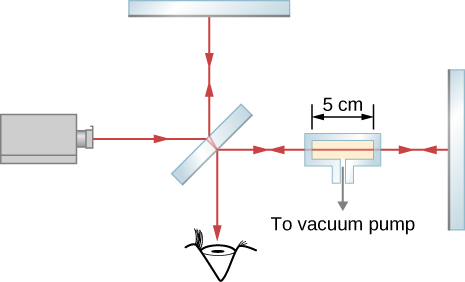
Picture shows a schematics of a set-up utilized to measure the refractive index of a gas. The glass chamber with a gas is placed in the Michelson interferometer between the half-silvered mirror M and mirror M1. The space inside the container is 5 cm wide.
Additional Problems
53. For 600-nm wavelength light and a slit separation of 0.12 mm, what are the angular positions of the first and third maxima in the double slit interference pattern?
54. If the light source in the preceding problem is changed, the angular position of the third maximum is found to be \(\displaystyle 0.57°\). What is the wavelength of light being used now?
55. Red light (\(\displaystyle λ=710.nm\)) illuminates double slits separated by a distance \(\displaystyle d=0.150mm\). The screen and the slits are 3.00 m apart.
(a) Find the distance on the screen between the central maximum and the third maximum.
(b) What is the distance between the second and the fourth maxima?
56. Two sources as in phase and emit waves with \(\displaystyle λ=0.42m\). Determine whether constructive or destructive interference occurs at points whose distances from the two sources are
(a) 0.84 and 0.42 m,
(b) 0.21 and 0.42 m,
(c) 1.26 and 0.42 m,
(d) 1.87 and 1.45 m,
(e) 0.63 and 0.84 m and
(f) 1.47 and 1.26 m.
57. Two slits \(\displaystyle 4.0×10^{−6}m\) apart are illuminated by light of wavelength 600 nm. What is the highest order fringe in the interference pattern?
58. Suppose that the highest order fringe that can be observed is the eighth in a double-slit experiment where 550-nm wavelength light is used. What is the minimum separation of the slits?
59. The interference pattern of a He-Ne laser light (\(\displaystyle λ=632.9nm\)) passing through two slits 0.031 mm apart is projected on a screen 10.0 m away. Determine the distance between the adjacent bright fringes.
60. Young’s double-slit experiment is performed immersed in water (\(\displaystyle n=1.333\)). The light source is a He-Ne laser, \(\displaystyle λ=632.9nm\) in vacuum.
(a) What is the wavelength of this light in water?
(b) What is the angle for the third order maximum for two slits separated by 0.100 mm.
61. A double-slit experiment is to be set up so that the bright fringes appear 1.27 cm apart on a screen 2.13 m away from the two slits. The light source was wavelength 500 nm. What should be the separation between the two slits?
62. An effect analogous to two-slit interference can occur with sound waves, instead of light. In an open field, two speakers placed 1.30 m apart are powered by a single-function generator producing sine waves at 1200-Hz frequency. A student walks along a line 12.5 m away and parallel to the line between the speakers. She hears an alternating pattern of loud and quiet, due to constructive and destructive interference. What is (a) the wavelength of this sound and (b) the distance between the central maximum and the first maximum (loud) position along this line?
63. A hydrogen gas discharge lamp emits visible light at four wavelengths, \(\displaystyle λ=\)410, 434, 486, and 656 nm. (a) If light from this lamp falls on a N slits separated by 0.025 mm, how far from the central maximum are the third maxima when viewed on a screen 2.0 m from the slits? (b) By what distance are the second and third maxima separated for \(\displaystyle l=486nm\)?
64. Monochromatic light of frequency \(\displaystyle 5.5×10^{14}Hz\) falls on 10 slits separated by 0.020 mm. What is the separation between the first and third maxima on a screen that is 2.0 m from the slits?
65. Eight slits equally separated by 0.149 mm is uniformly illuminated by a monochromatic light at \(\displaystyle λ=523nm\). What is the width of the central principal maximum on a screen 2.35 m away?
66. Eight slits equally separated by 0.149 mm is uniformly illuminated by a monochromatic light at \(\displaystyle λ=523nm\). What is the intensity of a secondary maxima compared to that of the principal maxima?
67. A transparent film of thickness 250 nm and index of refraction of 1.40 is surrounded by air. What wavelength in a beam of white light at near-normal incidence to the film undergoes destructive interference when reflected?
68. An intensity minimum is found for 450 nm light transmitted through a transparent film (\(\displaystyle n=1.20\)) in air.
(a) What is minimum thickness of the film?
(b) If this wavelength is the longest for which the intensity minimum occurs, what are the next three lower values of \(\displaystyle λ\) for which this happens?
69. A thin film with \(\displaystyle n=1.32\) is surrounded by air. What is the minimum thickness of this film such that the reflection of normally incident light with \(\displaystyle λ=500nm\) is minimized?
70. Repeat your calculation of the previous problem with the thin film placed on a flat glass (\(\displaystyle n=1.50\)) surface.
71. After a minor oil spill, a think film of oil (\(\displaystyle n=1.40\)) of thickness 450 nm floats on the water surface in a bay. (a) What predominant color is seen by a bird flying overhead? (b) What predominant color is seen by a seal swimming underwater?
72. A microscope slide 10 cm long is separated from a glass plate at one end by a sheet of paper. As shown below, the other end of the slide is in contact with the plate. he slide is illuminated from above by light from a sodium lamp (\(\displaystyle λ=589nm\)), and 14 fringes per centimeter are seen along the slide. What is the thickness of the piece of paper? Picture shows a microscope slide that touches the glass plate at one end and is separated from it at another end by a sheet of paper.
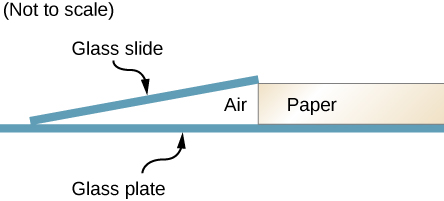
73. Suppose that the setup of the preceding problem is immersed in an unknown liquid. If 18 fringes per centimeter are now seen along the slide, what is the index of refraction of the liquid?
74. A thin wedge filled with air is produced when two flat glass plates are placed on top of one another and a slip of paper is inserted between them at one edge. Interference fringes are observed when monochromatic light falling vertically on the plates are seen in reflection. Is the first fringe near the edge where the plates are in contact a bright fringe or a dark fringe? Explain.
75. Two identical pieces of rectangular plate glass are used to measure the thickness of a hair. The glass plates are in direct contact at one edge and a single hair is placed between them hear the opposite edge. When illuminated with a sodium lamp (\(\displaystyle λ=589nm\)), the hair is seen between the 180th and 181st dark fringes. What are the lower and upper limits on the hair’s diameter?
76. Two microscope slides made of glass are illuminated by monochromatic (\(\displaystyle λ=589nm\)) light incident perpendicularly. The top slide touches the bottom slide at one end and rests on a thin copper wire at the other end, forming a wedge of air. The diameter of the copper wire is 29.45μm. How many bright fringes are seen across these slides?
77. A good quality camera “lens” is actually a system of lenses, rather than a single lens, but a side effect is that a reflection from the surface of one lens can bounce around many times within the system, creating artifacts in the photograph. To counteract this problem, one of the lenses in such a system is coated with a thin layer of material (\(\displaystyle n=1.28\)) on one side. The index of refraction of the lens glass is 1.68. What is the smallest thickness of the coating that reduces the reflection at 640 nm by destructive interference? (In other words, the coating’s effect is to be optimized for \(\displaystyle λ=640nm\).)
78. Constructive interference is observed from directly above an oil slick for wavelengths (in air) 440 nm and 616 nm. The index of refraction of this oil is \(\displaystyle n=1.54\). What is the film’s minimum possible thickness?
79. A soap bubble is blown outdoors. What colors (indicate by wavelengths) of the reflected sunlight are seen enhanced? The soap bubble has index of refraction 1.36 and thickness 380 nm.
80. A Michelson interferometer with a He-Ne laser light source (\(\displaystyle λ=632.8nm\)) projects its interference pattern on a screen. If the movable mirror is caused to move by \(\displaystyle 8.54μm\), how many fringes will be observed shifting through a reference point on a screen?
81. An experimenter detects 251 fringes when the movable mirror in a Michelson interferometer is displaced. The light source used is a sodium lamp, wavelength 589 nm. By what distance did the movable mirror move?
82. A Michelson interferometer is used to measure the wavelength of light put through it. When the movable mirror is moved by exactly 0.100 mm, the number of fringes observed moving through is 316. What is the wavelength of the light?
83. A 5.08-cm-long rectangular glass chamber is inserted into one arm of a Michelson interferometer using a 633-nm light source. This chamber is initially filled with air (\(\displaystyle n=1.000293\)) at standard atmospheric pressure but the air is gradually pumped out using a vacuum pump until a near perfect vacuum is achieved. How many fringes are observed moving by during the transition?
84. Into one arm of a Michelson interferometer, a plastic sheet of thickness \(\displaystyle 75μm\) is inserted, which causes a shift in the interference pattern by 86 fringes. The light source has wavelength of 610 nm in air. What is the index of refraction of this plastic?
85. The thickness of an aluminum foil is measured using a Michelson interferometer that has its movable mirror mounted on a micrometer. There is a difference of 27 fringes in the observed interference pattern when the micrometer clamps down on the foil compared to when the micrometer is empty. Calculate the thickness of the foil?
86. The movable mirror of a Michelson interferometer is attached to one end of a thin metal rod of length 23.3 mm. The other end of the rod is anchored so it does not move. As the temperature of the rod changes from \(\displaystyle 15°C\) to \(\displaystyle 25C\), a change of 14 fringes is observed. The light source is a He Ne laser, \(\displaystyle λ=632.8nm\). What is the change in length of the metal bar, and what is its thermal expansion coefficient?
87. In a thermally stabilized lab, a Michelson interferometer is used to monitor the temperature to ensure it stays constant. The movable mirror is mounted on the end of a 1.00-m-long aluminum rod, held fixed at the other end. The light source is a He Ne laser, \(\displaystyle λ=632.8nm\). The resolution of this apparatus corresponds to the temperature difference when a change of just one fringe is observed. What is this temperature difference?
88. A 65-fringe shift results in a Michelson interferometer when a \(\displaystyle 42.0-μm\) film made of an unknown material is placed in one arm. The light source has wavelength 632.9 nm. Identify the material using the indices of refraction found in Table 1.1.
Challenge Problems
89. Determine what happens to the double-slit interference pattern if one of the slits is covered with a thin, transparent film whose thickness is λ/[2(n−1)]λ/[2(n−1)], where λλ is the wavelength of the incident light and n is the index of refraction of the film.
90. Fifty-one narrow slits are equally spaced and separated by 0.10 mm. The slits are illuminated by blue light of wavelength 400 nm. What is angular position of the twenty-fifth secondary maximum? What is its peak intensity in comparison with that of the primary maximum?
91. A film of oil on water will appear dark when it is very thin, because the path length difference becomes small compared with the wavelength of light and there is a phase shift at the top surface. If it becomes dark when the path length difference is less than one-fourth the wavelength, what is the thickest the oil can be and appear dark at all visible wavelengths? Oil has an index of refraction of 1.40.
92. Figure 3.14 shows two glass slides illuminated by monochromatic light incident perpendicularly. The top slide touches the bottom slide at one end and rests on a 0.100-mm-diameter hair at the other end, forming a wedge of air. (a) How far apart are the dark bands, if the slides are 7.50 cm long and 589-nm light is used? (b) Is there any difference if the slides are made from crown or flint glass? Explain.
93. Figure 3.14 shows two 7.50-cm-long glass slides illuminated by pure 589-nm wavelength light incident perpendicularly. The top slide touches the bottom slide at one end and rests on some debris at the other end, forming a wedge of air. How thick is the debris, if the dark bands are 1.00 mm apart?
94. A soap bubble is 100 nm thick and illuminated by white light incident at a \(\displaystyle 45°\) angle to its surface. What wavelength and color of visible light is most constructively reflected, assuming the same index of refraction as water?
95. An oil slick on water is 120 nm thick and illuminated by white light incident at a \(\displaystyle 45°\) angle to its surface. What color does the oil appear (what is the most constructively reflected wavelength), given its index of refraction is 1.40?


