2.2: Equivalence of Gravitational and Inertial Mass
( \newcommand{\kernel}{\mathrm{null}\,}\)
We find experimentally that both gravitational and inertial mass are conserved to a high degree of precision for a great number of processes, including chemical reactions, melting, boiling, soaking up water with a sponge, and rotting of meat and vegetables. Now it's logically possible that both gravitational and inertial mass are conserved, but that there is no particular relationship between them, in which case we would say that they are separately conserved. On the other hand, the two conservation laws may be redundant, like having one law against murder and another law against killing people!
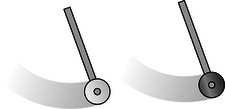
Figure a: The two pendulum bobs are constructed with equal gravitational masses. If their inertial masses are also equal, then each pendulum should take exactly the same amount of time per swing.
Here's an experiment that gets at the issue: stand up now and drop a coin and one of your shoes side by side. I used a 400-gram shoe and a 2-gram penny, and they hit the floor at the same time as far as I could tell by eye. This is an interesting result, but a physicist and an ordinary person will find it interesting for different reasons.
The layperson is surprised, since it would seem logical that heaver objects would always fall faster than light ones. However, it's fairly easy to prove that if air friction is negligible, any two objects made of the same substance must have identical motion when they fall. For instance, a 2-kg copper mass must exhibit the same falling motion as a 1-kg copper mass, because nothing would be changed by physically joining together two 1-kg copper masses to make a single 2-kg copper mass. Suppose, for example, that they are joined with a dab of glue; the glue isn't under any strain, because the two masses are doing the same thing side by side. Since the glue isn't really doing anything, it makes no difference whether the masses fall separately or side by side.2
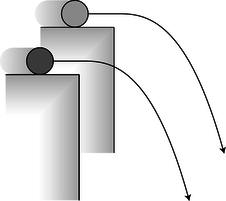
Figure b: If the cylinders have slightly unequal ratios of inertial to gravitational mass, their trajectories will be a little different.
What a physicist finds remarkable about the shoe-and-penny experiment is that it came out the way it did even though the shoe and the penny are made of different substances. There is absolutely no theoretical reason why this should be true. We could say that it happens because the greater gravitational mass of the shoe is exactly counteracted by its greater inertial mass, which makes it harder for gravity to get it moving, but that just leaves us wondering why inertial mass and gravitational mass are always in proportion to each other. It's possible that they are only approximately equivalent. Most of the mass of ordinary matter comes from neutrons and protons, and we could imagine, for instance, that neutrons and protons do not have exactly the same ratio of gravitational to inertial mass. This would show up as a different ratio of gravitational to inertial mass for substances containing different proportions of neutrons and protons.
Galileo did the first numerical experiments on this issue in the seventeenth century by rolling balls down inclined planes, although he didn't think about his results in these terms. A fairly easy way to improve on Galileo's accuracy is to use pendulums with bobs made of different materials. Suppose, for example, that we construct an aluminum bob and a brass bob, and use a double-pan balance to verify to good precision that their gravitational masses are equal. If we then measure the time required for each pendulum to perform a hundred cycles, we can check whether the results are the same. If their inertial masses are unequal, then the one with a smaller inertial mass will go through each cycle faster, since gravity has an easier time accelerating and decelerating it. With this type of experiment, one can easily verify that gravitational and inertial mass are proportional to each other to an accuracy of 10−3 or 10−4.
In 1889, the Hungarian physicist Roland Eötvös used a slightly different approach to verify the equivalence of gravitational and inertial mass for various substances to an accuracy of about 10−8, and the best such experiment, figure d, improved on even this phenomenal accuracy, bringing it to the 10−12 level.3 In all the experiments described so far, the two objects move along similar trajectories: straight lines in the penny-and-shoe and inclined plane experiments, and circular arcs in the pendulum version. The Eötvös-style experiment looks for differences in the objects' trajectories. The concept can be understood by imagining the following simplified version. Suppose, as in figure b, we roll a brass cylinder off of a tabletop and measure where it hits the floor, and then do the same with an aluminum cylinder, making sure that both of them go over the edge with precisely the same velocity. An object with zero gravitational mass would fly off straight and hit the wall, while an object with zero inertial mass would make a sudden 90-degree turn and drop straight to the floor. If the aluminum and brass cylinders have ordinary, but slightly unequal, ratios of gravitational to inertial mass, then they will follow trajectories that are just slightly different. In other words, if inertial and gravitational mass are not exactly proportional to each other for all substances, then objects made of different substances will have different trajectories in the presence of gravity.
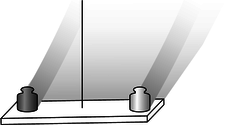
c / A simplified drawing of an Eötvös-style experiment. If the two masses, made out of two different substances, have slightly different ratios of inertial to gravitational mass, then the apparatus will twist slightly as the earth spins.
A simplified drawing of a practical, high-precision experiment is shown in figure c. Two objects made of different substances are balanced on the ends of a bar, which is suspended at the center from a thin fiber. The whole apparatus moves through space on a complicated, looping trajectory arising from the rotation of the earth superimposed on the earth's orbital motion around the sun. Both the earth's gravity and the sun's gravity act on the two objects. If their inertial masses are not exactly in proportion to their gravitational masses, then they will follow slightly different trajectories through space, which will result in a very slight twisting of the fiber between the daytime, when the sun's gravity is pulling upward, and the night, when the sun's gravity is downward. Figure d shows a more realistic picture of the apparatus.
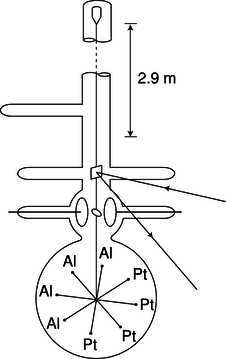
Figure d: A more realistic drawing of Braginskii and Panov's experiment. The whole thing was encased in a tall vacuum tube, which was placed in a sealed basement whose temperature was controlled to within 0.02°\textup{C}. The total mass of the platinum and aluminum test masses, plus the tungsten wire and the balance arms, was only 4.4 g. To detect tiny motions, a laser beam was bounced off of a mirror attached to the wire. There was so little friction that the balance would have taken on the order of several years to calm down completely after being put in place; to stop these vibrations, static electrical forces were applied through the two circular plates to provide very gentle twists on the ellipsoidal mass between them. After Braginskii and Panov.
This type of experiment, in which one expects a null result, is a tough way to make a career as a scientist. If your measurement comes out as expected, but with better accuracy than other people had previously achieved, your result is publishable, but won't be considered earth-shattering. On the other hand, if you build the most sensitive experiment ever, and the result comes out contrary to expectations, you're in a scary situation. You could be right, and earn a place in history, but if the result turns out to be due to a defect in your experiment, then you've made a fool of yourself.
Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


