04. Circular Motion
- Page ID
- 444
Circular Motion
If the acceleration of an object is not constant, in either magnitude or direction, the development of a kinematic description necessitates the use of calculus. A very common class of motion, in which the acceleration is guaranteed to change in at least direction, is the motion of an object on a circular path. Let's examine general circular motion in more detail before we attempt to describe a specific situation.
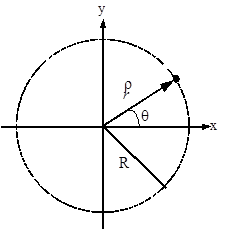
The x- and y-position of the object moving along a circular path of radius R can always be described by the functions:
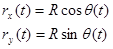
assuming the origin of the coordinate system is placed at the center of the circle.
Defining angular position, angular velocity and angular acceleration
Angular Position
The function q(t) specifies the angular position of the object, and is typically measured in radians. It specifies where, along the circle, the object is at every instant of time. For example, if q(t) is a constant, the object doesn't move. if q(t) is a linear function of time, the object moves with constant velocity around the circle. If q(t) is a more complex function, the object speeds up or slows down as it moves around the circle.
Angular Velocity
The rate at which q(t) is changing, 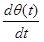 , is termed the angular velocity of the object, and denoted w(t). (w is the lower-case Greek letter "omega".) Since w(t) is the rate at which the angular position is changing, it has units of rad/s.
, is termed the angular velocity of the object, and denoted w(t). (w is the lower-case Greek letter "omega".) Since w(t) is the rate at which the angular position is changing, it has units of rad/s.
Angular Acceleration
The rate at which w(t) is changing, 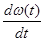 , is termed the angular acceleration of the object, and denoted a(t). (a is the lower-case Greek letter "alpha".) Since a(t) is the rate at which the angular velocity is changing, it has units rad/s2.
, is termed the angular acceleration of the object, and denoted a(t). (a is the lower-case Greek letter "alpha".) Since a(t) is the rate at which the angular velocity is changing, it has units rad/s2.
Deriving Relationships for velocity and acceleration
Now that we have the definitions of the angular quantities out of the way, let's determine the velocity and acceleration of an object undergoing circular motion. I'll begin by writing the position function in 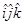 notation, common "short-hand" method of writing the x-,
notation, common "short-hand" method of writing the x-,
y-, and z- components of a vector all together. In this notation, the 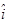 simply stands for the x-component, the
simply stands for the x-component, the 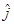 for the y-component, and the
for the y-component, and the 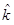 for any z-component. Hold onto your hat and try not to get lost in the calculus.
for any z-component. Hold onto your hat and try not to get lost in the calculus.
Position
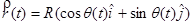
Velocity
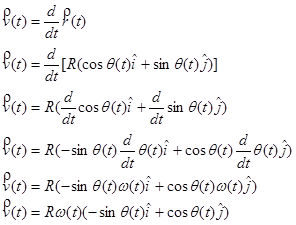
Acceleration
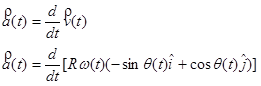
Remembering to use the chain rule for differentiation,
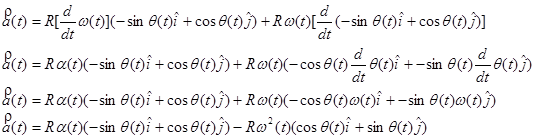
These relationships for velocity and acceleration look intimidating, but are actually rather simple. (You don't have to believe me just yet...) The problem is that they are written using an awkward choice of coordinate system. In a previous Model, we used inclined coordinates for situations involving objects moving on an inclined surface. For an object moving in a circle, it's almost as if the surface upon which the object moves is continually changing its angle of incline! Perhaps we whould use a coordinate system in which the orientation of the system continually changes, always keeping one axis parallel and one axis perpendicular to the motion. This is exactly what we will do. This coordinate system is referred to as the polar coordinate system.


