12.4: Ampère's Law In Differential Form (Optional)
( \newcommand{\kernel}{\mathrm{null}\,}\)
11.4.1 The curl operator
The differential form of Gauss' law is more physically satisfying than the integral form, because it relates the charges that are present at some point to the properties of the electric field at the same point. Likewise, it would be more attractive to have a differential version of Ampère's law that would relate the currents to the magnetic field at a single point.
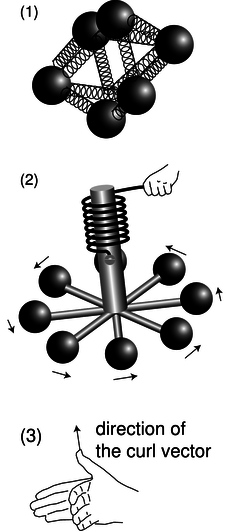
a / The div-meter, 1, and the curl-meter, 2 and 3.
Intuitively, the divergence was based on the idea of the div-meter, a/1. The corresponding device for measuring the curliness of a field is the curl-meter, a/2. If the field is curly, then the torques on the charges will not cancel out, and the wheel will twist against the resistance of the spring. If your intuition tells you that the curlmeter will never do anything at all, then your intuition is doing a beautiful job on static fields; for nonstatic fields, however, it is perfectly possible to get a curly electric field.
Gauss' law in differential form relates divE, a scalar, to the charge density, another scalar. Ampère's law, however, deals with directions in space: if we reverse the directions of the currents, it makes a difference. We therefore expect that the differential form of Ampère's law will have vectors on both sides of the equal sign, and we should be thinking of the curl-meter's result as a vector. First we find the orientation of the curl-meter that gives the strongest torque, and then we define the direction of the curl vector using the right-hand rule shown in figure a/3.
To convert the div-meter concept to a mathematical definition, we found the infinitesimal flux, dΦ through a tiny cubical Gaussian surface containing a volume dv. By analogy, we imagine a tiny square Ampèrian surface with infinitesimal area dA. We assume this surface has been oriented in order to get the maximum circulation. The area vector dA will then be in the same direction as the one defined in figure a/3. Ampère's law is
The complete set of Maxwell's equations in differential form is collected on page 914.
11.4.2 Properties of the curl operator
Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


