1.6D: Field on the Axis of and in the Plane of a Charged Ring

Field on the axis of a charged ring.

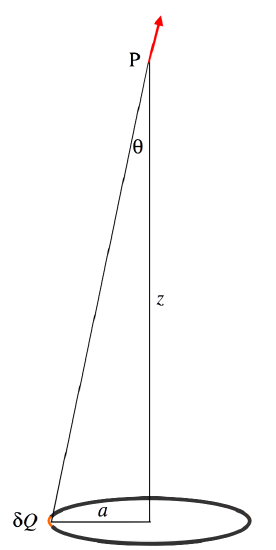
Ring, radius $a$, charge $Q$. Field at P from element of charge $δQ = \dfrac{\delta Q}{4\pi\epsilon_0 (a^2+z^2)}$. Vertical component of this $= \dfrac{\delta Q \cos \theta}{4\pi\epsilon_0 (a^2+z^2)}=\dfrac{\delta Qz}{4\pi\epsilon_0 (a^2+z^2)^{3/2}}$. Integrate for entire ring:

Field $E = \dfrac{Q}{4\pi\epsilon_0}\dfrac{z}{(a^2+z^2)^{3/2}}$.

In terms of dimensionless variables:

$$E=\dfrac{z}{(1+z^2)^{3/2}}.$$

where E is in units of $\dfrac{Q}{4\pi\epsilon_0 a^2}$, and $z$ is in units of $a$.

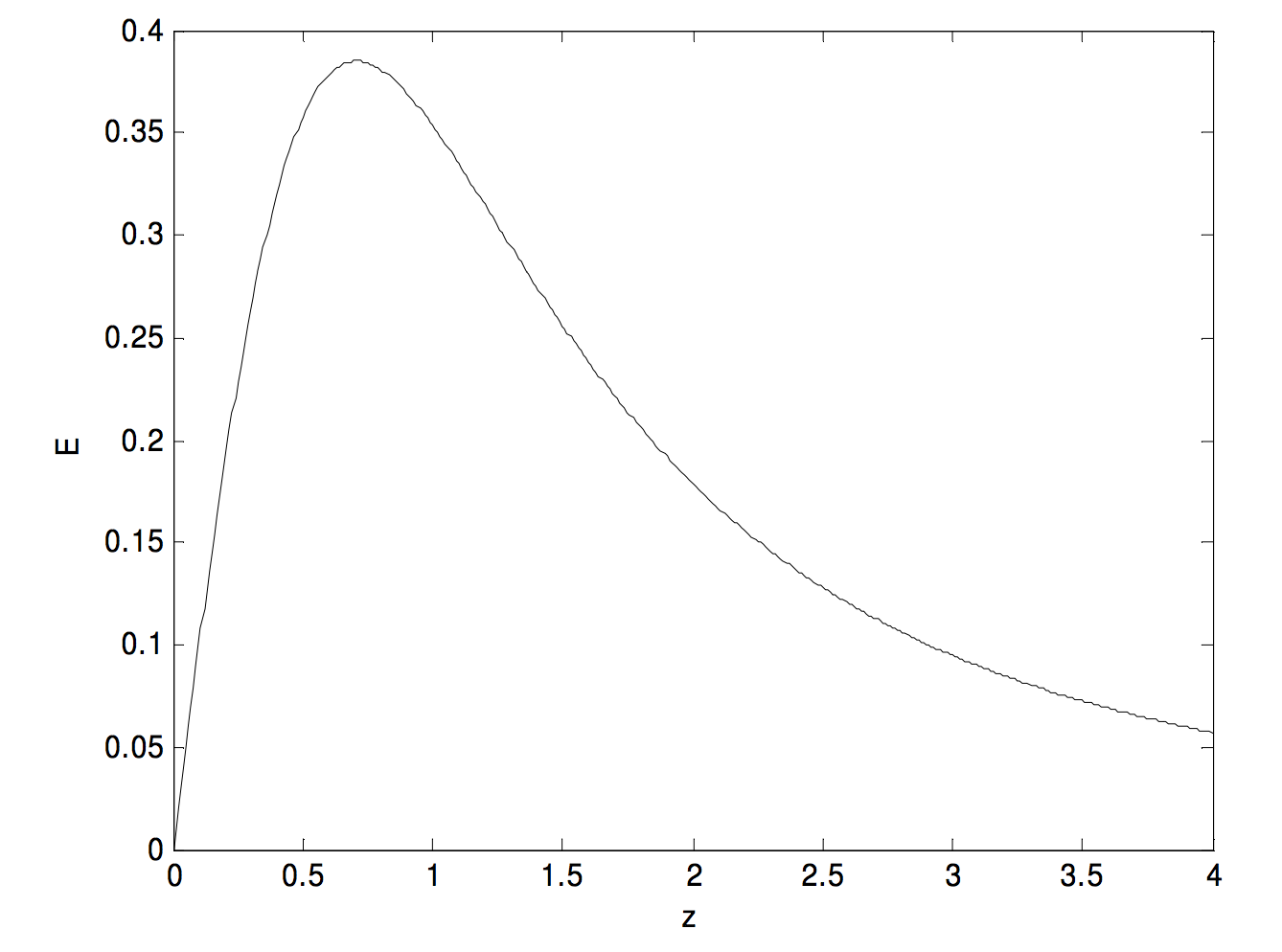
From calculus, we find that this reaches a maximum value of $\dfrac{2\sqrt{3}}{9}=0.3849$ at $z=1/\sqrt{2}=0.7071$.

It reaches half of its maximum value where $\dfrac{z}{(1+z^2)^{3/2}}=\dfrac{\sqrt{3}}{9}$.

That is, $3-72Z+9Z^2+3Z^2=0$, where $Z=z^2$.

The two positive solution are $Z = 0.041889 \text{ and }3.596267$.

That is, $z = 0.2047 \text{ and }1.8964$.

Field in the plane of a charged ring.

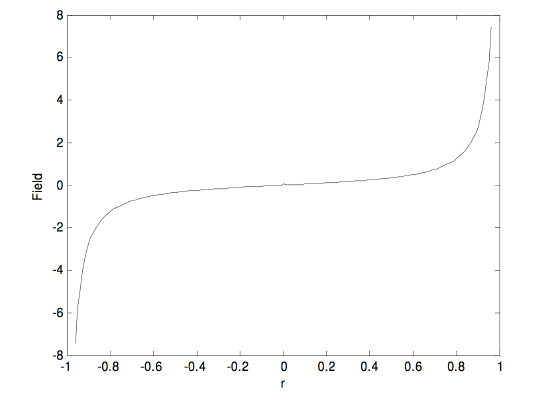
We suppose that we have a ring of radius $a$ bearing a charge $Q$. We shall try to find the field at a point in the plane of the ring and at a distance $r (0 ≤ r < a)$ from the centre of the ring.

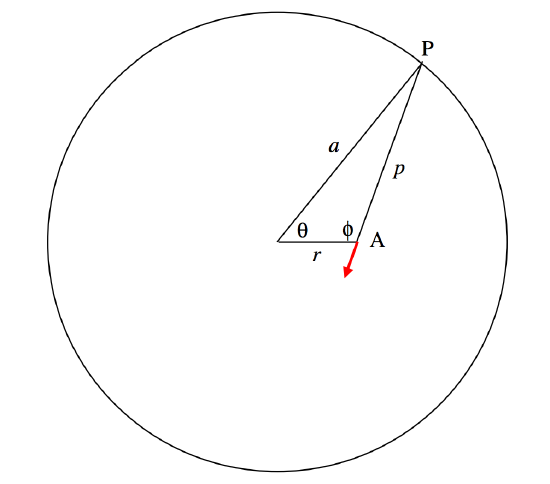
Consider an element $δθ$ of the ring at P. The charge on it is $\dfrac{Q\delta \theta}{2\pi}$. The field at A from this element of charge is

$$\dfrac{1}{4\pi\epsilon_0}\cdot \dfrac{Q\delta\theta}{2\pi}\cdot \dfrac{1}{a^2+r^2-2ar\cos \theta}=\dfrac{Q}{4\pi\epsilon_0 .2\pi a^2}\cdot \dfrac{\delta\theta}{b-c\cos \theta},$$

where $b=1+r^2/a^2$ and $c = 2r / a$. The component of this toward the centre is

$-\dfrac{Q}{4\pi\epsilon_0 .2 \pi a^2}\cdot\dfrac{\cos \phi \delta\theta}{b-c\cos \theta}$.

To find the field at A due to the entire ring, we must express $\phi$ in terms of $θ$, $r$ and $a$, and integrate with respect to $θ \text{ from }0 \text{ to }2π$ (or from $0 \text{ to }π$ and double it). The necessary relations are

$$p^2=a^2+r^2-2ar\cos \theta$$

$$\cos \phi = \dfrac{r^2+p^2-a^2}{2rp}.$$

The result of the numerical integration is shown below, in which the field is expressed in units of $Q/(4\pi\epsilon_0 a^2)$ and $r$ is in units of $a$.