2.2B: Spherical Charge Distributions
- Page ID
- 5836
Outside any spherically-symmetric charge distribution, the field is the same as if all the charge were concentrated at a point in the centre, and so, then, is the potential. Thus
\[V=\frac{Q}{4\pi\epsilon_0 r}.\tag{2.2.3}\]
Inside a hollow spherical shell of radius a and carrying a charge \(Q\) the field is zero, and therefore the potential is uniform throughout the interior, and equal to the potential on the surface, which is
\[V=\frac{Q}{4\pi\epsilon_0 a}.\tag{2.2.4}\]
A solid sphere of radius a bearing a charge \(Q\) that is uniformly distributed throughout the sphere is easier to imagine than to achieve in practice, but, for all we know, a proton might be like this (it might be – but it isn’t!), so let’s calculate the field at a point P inside the sphere at a distance \((r < a)\) from the centre. See Figure \(II.1\)
We can do this in two parts. First the potential from the part of the sphere “below” P. If the charge is uniformly distributed throughout the sphere, this is just \(\frac{Q_r}{4\pi\epsilon_0 r}\). Here \(Q_r\) is the charge contained within radius \(r\), which, if the charge is uniformly distributed throughout the sphere, is \(Q(r^3/a^3)\). Thus, that part of the potential is \(\frac{Qr^2}{4\pi\epsilon_0 a^3}\).
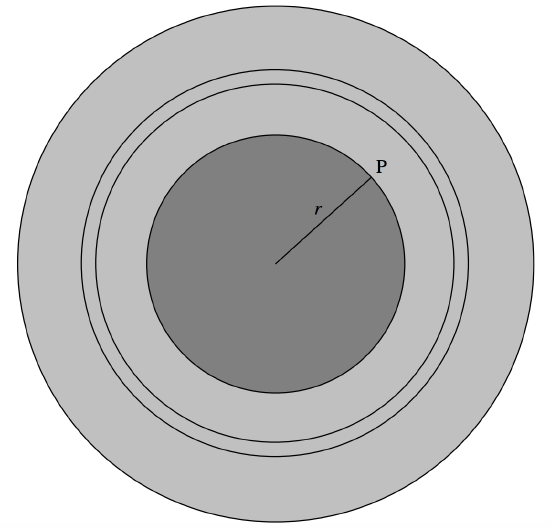
\(\text{FIGURE II.1}\)
Next, we calculate the contribution to the potential from the charge “above” P. Consider an elemental shell of radii \(x ,\, x + δx\). The charge held by it is \(\delta Q = \frac{4\pi x^2 \delta x}{\frac{4}{3}\pi a^3}\times Q=\frac{3Qx^2 \delta x}{a^3}\). The contribution to the potential at P from the charge in this elemental shell is \(\frac{\delta Q}{4\pi\epsilon_0 x}=\frac{3Qx\delta x}{4\pi\epsilon_0 a^3}\). The contribution to the potential from all the charge “above” P is \(\frac{3Q}{4\pi\epsilon_0 a^3}\int_r^a x\,dx=\frac{3Q(a^2-r^2)}{4\pi\epsilon_0 2a^3}\). Adding together the two parts of the potential, we obtain
\[V=\frac{Q}{8\pi\epsilon_0 a^3}(3a^2-r^2).\tag{2.2.5}\]


