5.18: Discharging a Capacitor Through a Resistor
( \newcommand{\kernel}{\mathrm{null}\,}\)
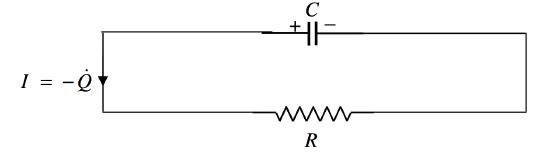
FIGURE V.24
What you have to be sure of in this section and the following section is to get the signs right. For example, if the charge held in the capacitor at some time is Q, then the symbol ˙Q, or dQ/dt means the rate of increase of Q with respect to time. If the capacitor is discharging, ˙Q is negative. Expressed otherwise, the symbol to be used for the rate at which a capacitor is losing charge is −˙Q.
In Figure V.24 a capacitor is discharging through a resistor, and the current as drawn is given by I=−˙Q. The potential difference across the plates of the capacitor is Q/C, and the potential difference across the resistor is IR=−˙QR.
Thus:
QC−IR=QC+˙QR=0
On separating the variables (Q and t) and integrating we obtain
∫QQ0dQQ=−1RC∫t0dt,
where Q0 is the charge in the capacitor at t=0.
Hence
Q=Q0e−t/(RC).
Here RC is the time constant. (Verify that it has the dimensions of time.) It is the time for the charge to be reduced to 1/e=36.8% of the initial charge. The half life of the charge is RCln2=0.6931RC.


