6.1: Introduction
( \newcommand{\kernel}{\mathrm{null}\,}\)
Most of us are familiar with the more obvious properties of magnets and compass needles. A magnet, often in the form of a short iron bar, will attract small pieces of iron such as nails and paper clips. Two magnets will either attract each other or repel each other, depending upon their orientation. If a bar magnet is placed on a sheet of paper and iron filings are scattered around the magnet, the iron filings arrange themselves in a manner that reminds us of the electric field lines surrounding an electric dipole. All in all, a bar magnet has some properties that are quite similar to those of an electric dipole. The region of space around a magnet within which it exerts its magic influence is called a magnetic field, and its geometry is rather similar to that of the electric field around an electric dipole – although its nature seems a little different, in that it interacts with iron filings and small bits of iron rather than with scraps of paper or pith-balls.
The resemblance of the magnetic field of a bar magnet to the electric field of an electric dipole was sometimes demonstrated in Victorian times by means of a Robison Ball-ended Magnet, which was a magnet shaped something like this:
FIGURE VI.1
The geometry of the magnetic field (demonstrated, for example, with iron filings) then greatly resembled the geometry of an electric dipole field. Indeed it looked as though a magnet had two poles (analogous to, but not the same as, electric charges), and that one of them acts as a source for magnetic field lines (i.e. field lines diverge from it), and the other acts as a sink (i.e. field lines converge to it). Rather than calling the poles “positive” and “negative”, we somewhat arbitrarily call them “north” and “south” poles, the “north” pole being the source and the “south” pole the sink. By experimenting with two or more magnets, we find that like poles repel and unlike poles attract.
We also observe that a freely-suspended magnet (i.e. a compass needle) will orient itself so that one end points approximately north, and the other points approximately south, and it is these poles that are called the “north” and “south” poles of the magnet.
Since unlike poles attract, we deduce (or rather William Gilbert, in his 1600 book De Magnete, Magneticisque Corporibus, et de Magno Magnete Tellure deduced) that Earth itself acts as a giant magnet, with a south magnetic pole somewhere in the Arctic and a north magnetic pole in the Antarctic. The Arctic magnetic pole is at present in Bathurst Island in northern Canada and is usually marked in atlases as the “North Magnetic Pole”, though magnetically it is a sink, rather than a source. The Antarctic magnetic pole is at present just offshore from Wilkes Land in the Antarctic continent. The Antarctic magnetic pole is a source, although it is usually marked in atlases as the “South Magnetic Pole”. Some people have advocated calling the end of a compass needle that points north the “north-seeking pole”, and the other end the “south-seeking pole. This has much to commend it, but usually, instead, we just call them the “north” and “south” poles. Unfortunately this means that the Earth’s magnetic pole in the Arctic is really a south magnetic pole, and the pole in the Antarctic is a north magnetic pole.
The resemblance of the magnetic field of a bar magnet to a dipole field, and the very close resemblance of a “Robison Ball-ended Magnet” to a dipole, with a point source (the north pole) at one end and a point sink (the south pole) at the other, is, however, deceptive.
In truth a magnetic field has no sources and no sinks. This is even expressed as one of Maxwell’s equations, div B=0, as being one of the defining characteristics of a magnetic field. The magnetic lines of force always form closed loops. Inside a bar magnet (even inside the connecting rod of a Robison magnet) the magnetic field lines are directed from the south pole to the north pole. If a magnet, even a Robison magnet, is cut in two, we do not isolate two separate poles. Instead each half of the magnet becomes a dipolar magnet itself.
All of this is very curious, and matters stood like this until Oersted made an outstanding discovery in 1820 (it is said while giving a university lecture in Copenhagen), which added what may have seemed like an additional complication, but which turned out to be in many ways a great simplification. He observed that, if an electric current is made to flow in a wire near to a freely suspended compass needle, the compass needle is deflected. Similarly, if a current flows in a wire that is free to move and is near to a fixed bar magnet, the wire experiences a force at right angles to the wire.
From this point on we understand that a magnetic field is something that is primarily associated with an electric current. All the phenomena associated with magnetized iron, nickel or cobalt, and “lodestones” and compass needles are somehow secondary to the fundamental phenomenon that an electric current is always surrounded by a magnetic field. Indeed, Ampère speculated that the magnetic field of a bar magnet may be caused by many circulating current loops within the iron. He was right! – the little current loops are today identified with electron spin.
If the direction of the magnetic field is taken to be the direction of the force on the north pole of a compass needle, Oersted’s observation showed that the magnetic field around a current is in the form of concentric circles surrounding the current. Thus in Figure VI.2, the current is assumed to be going away from you at right angles to the plane of your computer screen (or of the paper, if you have printed this page out), and the magnetic field lines are concentric circles around the current,
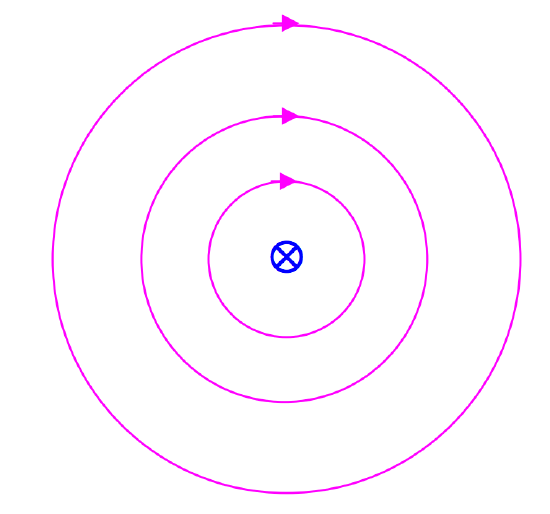
FIGURE VI.2
In the remainder of this chapter, we shall no longer be concerned with magnets, compass needles and lodestones. These may come in a later chapter. In the remainder of this chapter we shall be concerned with the magnetic field that surrounds an electric current.


