6.5: Magnetic Field Near a Long, Straight, Current-carrying Conductor
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider a point P at a distance a from a conductor carrying a current I (Figure VI.4).
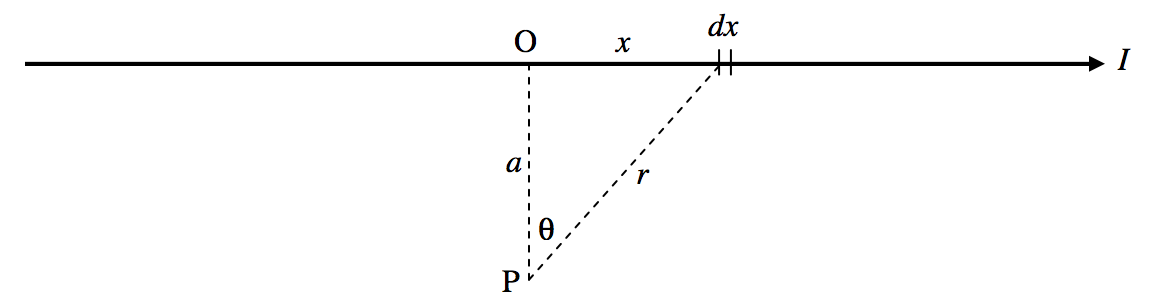
FIGURE VI.4
The contribution to the magnetic field at P from the elemental length dx is
dB=μ4π⋅Idxcosθr2.
(Look at the way I have drawn θ if you are worried about the cosine.)
Here I have omitted the subscript zero on the permeability to allow for the possibility that the wire is immersed in a medium in which the permeability is not the same as that of a vacuum. (The permeability of liquid oxygen, for example, is slightly greater than that of free space.) The direction of the field at P is into the plane of the “paper” (or of your computer screen).
We need to express this in terms of one variable, and we’ll choose θ. We can see that r=asecθ and x=atanθ so that dx=asec2θdθ. Thus Equation ??? becomes
dB=μI4πasinθdθ.
Upon integrating this from −π/2 to +π/2 (or from 0 to π/2 and then double it), we find that the field at P is
B=μI2πa.
Note the 2π in this problem with cylindrical symmetry.


