3.3: Irreversibility and Poincaré Recurrence

$\newcommand\bes{\begin{equation}\begin{split}}$
$\newcommand\ltwid{\propto}$
$\newcommand\ees{\end{split}\end{equation}}$
$\newcommand\mib{\mathbf}$
$\newcommand\Sa{\textsf a}$
$\newcommand\Sb{\textsf b}$
$\newcommand\Sc{\textsf c}$
$\newcommand\Sd{\textsf d}$
$\newcommand\Se{\textsf e}$
$\newcommand\Sf{\textsf f}$
$\newcommand\Sg{\textsf g}$
$\newcommand\Sh{\textsf h}$
$\newcommand\Si{\textsf i}$
$\newcommand\Sj{\textsf j}$
$\newcommand\Sk{\textsf k}$
$\newcommand\Sl{\textsf l}$
$\newcommand\Sm{\textsf m}$
$\newcommand\Sn{\textsf n}$
$\newcommand\So{\textsf o}$
$\newcommand\Sp{\textsf p}$
$\newcommand\Sq{\textsf q}$
$\newcommand\Sr{\textsf r}$
$\newcommand\Ss{\textsf s}$
$\newcommand\St{\textsf t}$
$\newcommand\Su{\textsf u}$
$\newcommand\Sv{\textsf v}$
$\newcommand\Sw{\textsf w}$
$\newcommand\Sx{\textsf x}$
$\newcommand\Sy{\textsf y}$
$\newcommand\Sz{\textsf z}$
$\newcommand\SA{\textsf A}$
$\newcommand\SB{\textsf B}$
$\newcommand\SC{\textsf C}$
$\newcommand\SD{\textsf D}$
$\newcommand\SE{\textsf E}$
$\newcommand\SF{\textsf F}$
$\newcommand\SG{\textsf G}$
$\newcommand\SH{\textsf H}$
$\newcommand\SI{\textsf I}$
$\newcommand\SJ{\textsf J}$
$\newcommand\SK{\textsf K}$
$\newcommand\SL{\textsf L}$
$\newcommand\SM{\textsf M}$
$\newcommand\SN{\textsf N}$
$\newcommand\SO{\textsf O}$
$\newcommand\SP{\textsf P}$
$\newcommand\SQ{\textsf Q}$
$\newcommand\SR{\textsf R}$
$\newcommand\SS{\textsf S}$
$\newcommand\ST{\textsf T}$
$\newcommand\SU{\textsf U}$
$\newcommand\SV{\textsf V}$
$\newcommand\SW{\textsf W}$
$\newcommand\SX{\textsf X}$
$\newcommand\SY{\textsf Y}$
$\newcommand\SZ{\textsf Z}$
$\newcommand\Ha{\hat a}$
$\newcommand\Hb{\hat b}$
$\newcommand\Hc{\hat c}$
$\newcommand\Hd{\hat d}$
$\newcommand\He{\hat e}$
$\newcommand\Hf{\hat f}$
$\newcommand\Hg{\hat g}$
$\newcommand\Hh{\hat h}$
$\newcommand\Hi{\hat \imath}$
$\newcommand\Hj{\hat \jmath}$
$\newcommand\Hk{\hat k}$
$\newcommand\Hl{\hat l}$
$\newcommand\Hm{\hat m}$
$\newcommand\Hn{\hat n}$
$\newcommand\Ho{\hat o}$
$\newcommand\Hp{\hat p}$
$\newcommand\Hq{\hat q}$
$\newcommand\Hr{\hat r}$
$\newcommand\Hs{\hat s}$
$\newcommand\Ht{\hat t}$
$\newcommand\Hu{\hat u}$
$\newcommand\Hv{\hat v}$
$\newcommand\Hw{\hat w}$
$\newcommand\Hx{\hat x}$
$\newcommand\Hy{\hat y}$
$\newcommand\Hz{\hat z}$
$\newcommand\HA{\hat A}$
$\newcommand\HB{\hat B}$
$\newcommand\HC{\hat C}$
$\newcommand\HD{\hat D}$
$\newcommand\HE{\hat E}$
$\newcommand\HF{\hat F}$
$\newcommand\HG{\hat G}$
$\newcommand\HH{\hat H}$
$\newcommand\HI{\hat I}$
$\newcommand\HJ{\hat J}$
$\newcommand\HK{\hat K}$
$\newcommand\HL{\hat L}$
$\newcommand\HM{\hat M}$
$\newcommand\HN{\hat N}$
$\newcommand\HO{\hat O}$
$\newcommand\HP{\hat P}$
$\newcommand\HQ{\hat Q}$
$\newcommand\HR{\hat R}$
$\newcommand\HS{\hat S}$
$\newcommand\HT{\hat T}$
$\newcommand\HU{\hat U}$
$\newcommand\HV{\hat V}$
$\newcommand\HW{\hat W}$
$\newcommand\HX{\hat X}$
$\newcommand\HY{\hat Y}$
$\newcommand\HZ{\hat Z}$
$\newcommand\Halpha{\hat\alpha}$
$\newcommand\Hbeta{\hat\beta}$
$\newcommand\Hgamma{\hat\gamma}$
$\newcommand\Hdelta{\hat\delta}$
$\newcommand\Hepsilon{\hat\epsilon}$
$\newcommand\Hvarepsilon{\hat\varepsilon}$
$\newcommand\Hzeta{\hat\zeta}$
$\newcommand\Heta{\hat\eta}$
$\newcommand\Htheta{\hat\theta}$
$\newcommand\Hvartheta{\hat\vartheta}$
$\newcommand\Hiota{\hat\iota}$
$\newcommand\Hkappa{\hat\kappa}$
$\newcommand\Hlambda{\hat\lambda}$
$\newcommand\Hmu{\hat\mu}$
$\newcommand\Hnu{\hat\nu}$
$\newcommand\Hxi{\hat\xi}$
$\newcommand\Hom{\hat\omicron}$
$\newcommand\Hpi{\hat\pi}$
$\newcommand\Hvarpi{\hat\varpi}$
$\newcommand\Hrho{\hat\rho}$
$\newcommand\Hvarrho{\hat\varrho}$
$\newcommand\Hsigma{\hat\sigma}$
$\newcommand\Hvarsigma{\hat\varsigma}$
$\newcommand\Htau{\var\tau}$
$\newcommand\Hupsilon{\hat\upsilon}$
$\newcommand\Hphi{\hat\phi}$
$\newcommand\Hvarphi{\hat\varphi}$
$\newcommand\Hchi{\hat\chi}$
$\newcommand\Hxhi{\hat\xhi}$
$\newcommand\Hpsi{\hat\psi}$
$\newcommand\Homega{\hat\omega}$
$\newcommand\HGamma{\hat\Gamma}$
$\newcommand\HDelta{\hat\Delta}$
$\newcommand\HTheta{\hat\Theta}$
$\newcommand\HLambda{\hat\Lambda}$
$\newcommand\HXi{\hat\Xi}$
$\newcommand\HPi{\hat\Pi}$
$\newcommand\HSigma{\hat\Sigma}$
$\newcommand\HUps{\hat\Upsilon}$
$\newcommand\HPhi{\hat\Phi}$
$\newcommand\HPsi{\hat\Psi}$
$\newcommand\HOmega{\hat\Omega}$
$\newcommand\xhat{\hat\Bx}$
$\newcommand\yhat{\hat\By}$
$\newcommand\zhat{\hat\Bz}$
$\newcommand\ehat{\hat\Be}$
$\newcommand\khat{\hat\Bk}$
$\newcommand\nhat{\hat\Bn}$
$\newcommand\rhat{\hat\Br}$
$\newcommand\phihat{\hat\Bphi}$
$\newcommand\thetahat{\hat\Btheta}$
$\newcommand\MA{\mathbb A}$
$\newcommand\MB{\mathbb B}$
$\newcommand\MC{\mathbb C}$
$\newcommand\MD{\mathbb D}$
$\newcommand\ME{\mathbb E}$
$\newcommand\MF{\mathbb F}$
$\newcommand\MG{\mathbb G}$
$\newcommand\MH{\mathbb H}$
$\newcommand\MI{\mathbb I}$
$\newcommand\MJ{\mathbb J}$
$\newcommand\MK{\mathbb K}$
$\newcommand\ML{\mathbb L}$
$\newcommand\MM{\mathbb M}$
$\newcommand\MN{\mathbb N}$
$\newcommand\MO{\mathbb O}$
$\newcommand\MP{\mathbb P}$
$\newcommand\MQ{\mathbb Q}$
$\newcommand\MR{\mathbb R}$
$\newcommand\MS{\mathbb S}$
$\newcommand\MT{\mathbb T}$
$\newcommand\MU{\mathbb U}$
$\newcommand\MV{\mathbb V}$
$\newcommand\MW{\mathbb W}$
$\newcommand\MX{\mathbb X}$
$\newcommand\MY{\mathbb Y}$
$\newcommand\MZ{\mathbb Z}$
$\newcommand\CA{\mathcal A}$
$\newcommand\CB{\mathcal B}$
$\newcommand\CC{\mathcal C}$
$\newcommand\CD{\mathcal D}$
$\newcommand\CE{\mathcal E}$
$\newcommand\CF{\mathcal F}$
$\newcommand\CG{\mathcal G}$
$\newcommand\CH{\mathcal H}$
$\newcommand\CI{\mathcal I}$
$\newcommand\CJ{\mathcal J}$
$\newcommand\CK{\mathcal K}$
$\newcommand\CL{\mathcal L}$
$\newcommand\CM{\mathcal M}$
$\newcommand\CN{\mathcal N}$
$\newcommand\CO{\mathcal O}$
$\newcommand\CP{\mathcal P}$
$\newcommand\CQ{\mathcal Q}$
$\newcommand\CR{\mathcal R}$
$\newcommand\CS{\mathcal S}$
$\newcommand\CT{\mathcal T}$
$\newcommand\CU{\mathcal U}$
$\newcommand\CV{\mathcal V}$
$\newcommand\CW{\mathcal W}$
$\newcommand\CX{\mathcal X}$
$\newcommand\CY{\mathcal Y}$
$\newcommand\CZ{\mathcal Z}$
$\newcommand\Fa{\mathfrak a}$
$\newcommand\Fb{\mathfrak b}$
$\newcommand\Fc{\mathfrak c}$
$\newcommand\Fd{\mathfrak d}$
$\newcommand\Fe{\mathfrak e}$
$\newcommand\Ff{\mathfrak f}$
$\newcommand\Fg{\mathfrak g}$
$\newcommand\Fh{\mathfrak h}$
$\newcommand\Fi{\mathfrak i}$
$\newcommand\Fj{\mathfrak j}$
$\newcommand\Fk{\mathfrak k}$
$\newcommand\Fl{\mathfrak l}$
$\newcommand\Fm{\mathfrak m}$
$\newcommand\Fn{\mathfrak n}$
$\newcommand\Fo{\mathfrak o}$
$\newcommand\Fp{\mathfrak p}$
$\newcommand\Fq{\mathfrak q}$
$\newcommand\Fr{\mathfrak r}$
$\newcommand\Fs{\mathfrak s}$
$\newcommand\Ft{\mathfrak t}$
$\newcommand\Fu{\mathfrak u}$
$\newcommand\Fv{\mathfrak v}$
$\newcommand\Fw{\mathfrak w}$
$\newcommand\Fx{\mathfrak x}$
$\newcommand\Fy{\mathfrak y}$
$\newcommand\Fz{\mathfrak z}$
$\newcommand\FA{\mathfrak A}$
$\newcommand\FB{\mathfrak B}$
$\newcommand\FC{\mathfrak C}$
$\newcommand\FD{\mathfrak D}$
$\newcommand\FE{\mathfrak E}$
$\newcommand\FF{\mathfrak F}$
$\newcommand\FG{\mathfrak G}$
$\newcommand\FH{\mathfrak H}$
$\newcommand\FI{\mathfrak I}$
$\newcommand\FJ{\mathfrak J}$
$\newcommand\FK{\mathfrak K}$
$\newcommand\FL{\mathfrak L}$
$\newcommand\FM{\mathfrak M}$
$\newcommand\FN{\mathfrak N}$
$\newcommand\FO{\mathfrak O}$
$\newcommand\FP{\mathfrak P}$
$\newcommand\FQ{\mathfrak Q}$
$\newcommand\FR{\mathfrak R}$
$\newcommand\FS{\mathfrak S}$
$\newcommand\FT{\mathfrak T}$
$\newcommand\FU{\mathfrak U}$
$\newcommand\FV{\mathfrak V}$
$\newcommand\FW{\mathfrak W}$
$\newcommand\FX{\mathfrak X}$
$\newcommand\FY{\mathfrak Y}$
$\newcommand\FZ{\mathfrak Z}$
$\newcommand\Da{\dot a}$
$\newcommand\Db{\dot b}$
$\newcommand\Dc{\dot c}$
$\newcommand\Dd{\dot d}$
$\newcommand\De{\dot e}$
$\newcommand\Df{\dot f}$
$\newcommand\Dg{\dot g}$
$\newcommand\Dh{\dot h}$
$\newcommand\Di{\dot \imath}$
$\newcommand\Dj{\dot \jmath}$
$\newcommand\Dk{\dot k}$
$\newcommand\Dl{\dot l}$
$\newcommand\Dm{\dot m}$
$\newcommand\Dn{\dot n}$
$\newcommand\Do{\dot o}$
$\newcommand\Dp{\dot p}$
$\newcommand\Dq{\dot q}$
$\newcommand\Dr{\dot r}$
$\newcommand\Ds{\dot s}$
$\newcommand\Dt{\dot t}$
$\newcommand\Du{\dot u}$
$\newcommand\Dv{\dot v}$
$\newcommand\Dw{\dot w}$
$\newcommand\Dx{\dot x}$
$\newcommand\Dy{\dot y}$
$\newcommand\Dz{\dot z}$
$\newcommand\DA{\dot A}$
$\newcommand\DB{\dot B}$
$\newcommand\DC{\dot C}$
$\newcommand\DD{\dot D}$
$\newcommand\DE{\dot E}$
$\newcommand\DF{\dot F}$
$\newcommand\DG{\dot G}$
$\newcommand\DH{\dot H}$
$\newcommand\DI{\dot I}$
$\newcommand\DJ{\dot J}$
$\newcommand\DK{\dot K}$
$\newcommand\DL{\dot L}$
$\newcommand\DM{\dot M}$
$\newcommand\DN{\dot N}$
$\newcommand\DO{\dot O}$
$\newcommand\DP{\dot P}$
$\newcommand\DQ{\dot Q}$
$\newcommand\DR{\dot R}$
$\newcommand\DS{\dot S}$
$\newcommand\DT{\dot T}$
$\newcommand\DU{\dot U}$
$\newcommand\DV{\dot V}$
$\newcommand\DW{\dot W}$
$\newcommand\DX{\dot X}$
$\newcommand\DY{\dot Y}$
$\newcommand\DZ{\dot Z}$
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\Dmu{\dot\mu}$
$\newcommand\Dnu{\dot\nu}$
$\newcommand\Dxi{\dot\xi}$
$\newcommand\Dom{\dot\omicron}$
$\newcommand\Dpi{\dot\pi}$
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\Drho{\dot\rho}$
$\newcommand\Dvarrho{\dot\varrho}$
$\newcommand\Dsigma{\dot\sigma}$
$\newcommand\Dvarsigma{\dot\varsigma}$
$\newcommand\Dtau{\var\tau}$
$\newcommand\Dupsilon{\dot\upsilon}$
$\newcommand\Dphi{\dot\phi}$
$\newcommand\Dvarphi{\dot\varphi}$
$\newcommand\Dchi{\dot\chi}$
$\newcommand\Dpsi{\dot\psi}$
$\newcommand\Domega{\dot\omega}$
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\DLambda{\dot\Lambda}$
$\newcommand\DXi{\dot\Xi}$
$\newcommand\DPi{\dot\Pi}$
$\newcommand\DSigma{\dot\Sigma}$
$\newcommand\DUps{\dot\Upsilon}$
$\newcommand\DPhi{\dot\Phi}$
$\newcommand\DPsi{\dot\Psi}$
$\newcommand\DOmega{\dot\Omega}$
$\newcommand\Va{\vec a}$
$\newcommand\Vb{\vec b}$
$\newcommand\Vc{\vec c}$
$\newcommand\Vd{\vec d}$
$\newcommand\Ve{\vec e}$
$\newcommand\Vf{\vec f}$
$\newcommand\Vg{\vec g}$
$\newcommand\Vh{\vec h}$
$\newcommand\Vi{\vec \imath}$
$\newcommand\Vj{\vec \jmath}$
$\newcommand\Vk{\vec k}$
$\newcommand\Vl{\vec l}$
$\newcommand\Vm{\vec m}$
$\newcommand\Vn{\vec n}$
$\newcommand\Vo{\vec o}$
$\newcommand\Vp{\vec p}$
$\newcommand\Vq{\vec q}$
$\newcommand\Vr{\vec r}$
$\newcommand\Vs{\vec s}$
$\newcommand\Vt{\vec t}$
$\newcommand\Vu{\vec u}$
$\newcommand\Vv{\vec v}$
$\newcommand\Vw{\vec w}$
$\newcommand\Vx{\vec x}$
$\newcommand\Vy{\vec y}$
$\newcommand\Vz{\vec z}$
$\newcommand\VA{\vec A}$
$\newcommand\VB{\vec B}$
$\newcommand\VC{\vec C}$
$\newcommand\VD{\vec D}$
$\newcommand\VE{\vec E}$
$\newcommand\VF{\vec F}$
$\newcommand\VG{\vec G}$
$\newcommand\VH{\vec H}$
$\newcommand\VI{\vec I}$
$\newcommand\VJ{\vec J}$
$\newcommand\VK{\vec K}$
$\newcommand\VL{\vec L}$
$\newcommand\VM{\vec M}$
$\newcommand\VN{\vec N}$
$\newcommand\VO{\vec O}$
$\newcommand\VP{\vec P}$
$\newcommand\VQ{\vec Q}$
$\newcommand\VR{\vec R}$
$\newcommand\VS{\vec S}$
$\newcommand\VT{\vec T}$
$\newcommand\VU{\vec U}$
$\newcommand\VV{\vec V}$
$\newcommand\VW{\vec W}$
$\newcommand\VX{\vec X}$
$\newcommand\VY{\vec Y}$
$\newcommand\VZ{\vec Z}$
$\newcommand\Valpha{\vec\alpha}$
$\newcommand\Vbeta{\vec\beta}$
$\newcommand\Vgamma{\vec\gamma}$
$\newcommand\Vdelta{\vec\delta}$
$\newcommand\Vepsilon{\vec\epsilon}$
$\newcommand\Vvarepsilon{\vec\varepsilon}$
$\newcommand\Vzeta{\vec\zeta}$
$\newcommand\Veta{\vec\eta}$
$\newcommand\Vtheta{\vec\theta}$
$\newcommand\Vvartheta{\vec\vartheta}$
$\newcommand\Viota{\vec\iota}$
$\newcommand\Vkappa{\vec\kappa}$
$\newcommand\Vlambda{\vec\lambda}$
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\VTheta{\vec\Theta}$
$\newcommand\VLambda{\vec\Lambda}$
$\newcommand\VXi{\vec\Xi}$
$\newcommand\VPi{\vec\Pi}$
$\newcommand\VSigma{\vec\Sigma}$
$\newcommand\VUps{\vec\Upsilon}$
$\newcommand\VPhi{\vec\Phi}$
$\newcommand\VPsi{\vec\Psi}$
$\newcommand\VOmega{\vec\Omega}$
$\newcommand\BA{\mib A}$
$\newcommand\BB{\mib B}$
$\newcommand\BC{\mib C}$
$\newcommand\BD{\mib D}$
$\newcommand\BE{\mib E}$
$\newcommand\BF{\mib F}$
$\newcommand\BG{\mib G}$
$\newcommand\BH{\mib H}$
$\newcommand\BI{\mib I}}$
$\newcommand\BJ{\mib J}$
$\newcommand\BK{\mib K}$
$\newcommand\BL{\mib L}$
$\newcommand\BM{\mib M}$
$\newcommand\BN{\mib N}$
$\newcommand\BO{\mib O}$
$\newcommand\BP{\mib P}$
$\newcommand\BQ{\mib Q}$
$\newcommand\BR{\mib R}$
$\newcommand\BS{\mib S}$
$\newcommand\BT{\mib T}$
$\newcommand\BU{\mib U}$
$\newcommand\BV{\mib V}$
$\newcommand\BW{\mib W}$
$\newcommand\BX{\mib X}$
$\newcommand\BY{\mib Y}$
$\newcommand\BZ{\mib Z}$
$\newcommand\Ba{\mib a}$
$\newcommand\Bb{\mib b}$
$\newcommand\Bc{\mib c}$
$\newcommand\Bd{\mib d}$
$\newcommand\Be{\mib e}$
$\newcommand\Bf{\mib f}$
$\newcommand\Bg{\mib g}$
$\newcommand\Bh{\mib h}$
$\newcommand\Bi{\mib i}$
$\newcommand\Bj{\mib j}$
$\newcommand\Bk{\mib k}$
$\newcommand\Bl{\mib l}$
$\newcommand\Bm{\mib m}$
$\newcommand\Bn{\mib n}$
$\newcommand\Bo{\mib o}$
$\newcommand\Bp{\mib p}$
$\newcommand\Bq{\mib q}$
$\newcommand\Br{\mib r}$
$\newcommand\Bs{\mib s}$
$\newcommand\Bt{\mib t}$
$\newcommand\Bu{\mib u}$
$\newcommand\Bv{\mib v}$
$\newcommand\Bw{\mib w}$
$\newcommand\Bx{\mib x}$
$\newcommand\By{\mib y}$
$\newcommand\Bz{\mib z}$\)
$\newcommand\vrh{\varrho}$
$\newcommand\vsig{\varsigma}$
$\newcommand\ups{\upsilon}$
$\newcommand\eps{\epsilon}$
$\newcommand\ve{\varepsilon}$
$\newcommand\vth{\vartheta}$
$\newcommand\vphi{\varphi}$
$\newcommand\xhi{\chi}$
$\newcommand\Ups{\Upsilon}$
$\newcommand\Balpha{\mib\alpha}$
$\newcommand\Bbeta{\mib\beta}$
$\newcommand\Bgamma{\mib\gamma}$
$\newcommand\Bdelta{\mib\delta}$
$\newcommand\Beps{\mib\epsilon}$
$\newcommand\Bve{\mib\varepsilon}$
$\newcommand\Bzeta{\mib\zeta}$
$\newcommand\Beta{\mib\eta}$
$\newcommand\Btheta{\mib\theta}$
$\newcommand\Bvth{\mib\vartheta}$
$\newcommand\Biota{\mib\iota}$
$\newcommand\Bkappa{\mib\kappa}$
$\newcommand\Blambda{\mib\lambda}$
$\newcommand\Bmu{\mib\mu}$
$\newcommand\Bnu{\mib\nu}$
$\newcommand\Bxi{\mib\xi}$
$\newcommand\Bom{\mib\omicron}$
$\newcommand\Bpi{\mib\pi}$
$\newcommand\Bvarpi{\mib\varpi}$
$\newcommand\Brho{\mib\rho}$
$\newcommand\Bvrh{\mib\varrho}$
$\newcommand\Bsigma{\mib\sigma}$
$\newcommand\Bvsig{\mib\varsigma}$
$\newcommand\Btau{\mib\tau}$
$\newcommand\Bups{\mib\upsilon}$
$\newcommand\Bphi{\mib\phi}$
$\newcommand\Bvphi{\mib\vphi}$
$\newcommand\Bchi{\mib\chi}$
$\newcommand\Bpsi{\mib\psi}$
$\newcommand\Bomega{\mib\omega}$
$\newcommand\BGamma{\mib\Gamma}$
$\newcommand\BDelta{\mib\Delta}$
$\newcommand\BTheta{\mib\Theta}$
$\newcommand\BLambda{\mib\Lambda}$
$\newcommand\BXi{\mib\Xi}$
$\newcommand\BPi{\mib\Pi}$
$\newcommand\BSigma{\mib\Sigma}$
$\newcommand\BUps{\mib\Upsilon}$
$\newcommand\BPhi{\mib\Phi}$
$\newcommand\BPsi{\mib\Psi}$
$\newcommand\BOmega{\mib\Omega}$
$\newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}$
$\newcommand\RGamma{ \Gamma}$
$\newcommand\RDelta{ \Delta}$
$\newcommand\RTheta{ \Theta}$
$\newcommand\RLambda{ \Lambda}$
$\newcommand\RXi{ \Xi}$
$\newcommand\RPi{ \Pi}$
$\newcommand\RSigma{ \Sigma}$
$\newcommand\RUps{ \Upsilon}$
$\newcommand\RPhi{ \Phi}$
$\newcommand\RPsi{ \Psi}$
$\newcommand\ROmega{ \Omega}$
$\newcommand\RA{ A}$
$\newcommand\RB{ B}$
$\newcommand\RC{ C}$
$\newcommand\RD{ D}$
$\newcommand\RE{ E}$
$\newcommand\RF{ F}$
$\newcommand\RG{ G}$
$\newcommand\RH{ H}$
$\newcommand\RI{ I}$
$\newcommand\RJ{ J}$
$\newcommand\RK{ K}$
$\newcommand\RL{ L}$
$\newcommand { M}$
$\newcommand\RN{ N}$
$\newcommand\RO{ O}$
$\newcommand\RP{ P}$
$\newcommand\RQ{ Q}$
$\newcommand\RR{ R}$
$\newcommand\RS{ S}$
$\newcommand\RT{ T}$
$\newcommand\RU{ U}$
$\newcommand\RV{ V}$
$\newcommand\RW{ W}$
$\newcommand\RX{ X}$
$\newcommand\RY{ Y}$
$\newcommand\RZ{ Z}$
$\newcommand\Ra{ a}$
$\newcommand\Rb{ b}$
$\newcommand\Rc{ c}$
$\newcommand\Rd{ d}$
$\newcommand\Re{ e}$
$\newcommand\Rf{ f}$
$\newcommand\Rg{ g}$
$\newcommand\Rh{ h}$
$\newcommand\Ri{ i}$
$\newcommand\Rj{ j}$
$\newcommand\Rk{ k}$
$\newcommand\Rl{ l}$
$\newcommand { m}$
$\newcommand\Rn{ n}$
$\newcommand\Ro{ o}$
$\newcommand\Rp{ p}$
$\newcommand\Rq{ q}$
$\newcommand\Rr{ r}$
$\newcommand\Rs{ s}$
$\newcommand\Rt{ t}$
$\newcommand\Ru{ u}$
$\newcommand\Rv{ v}$
$\newcommand\Rw{ w}$
$\newcommand\Rx{ x}$
$\newcommand\Ry{ y}$
$\newcommand\Rz{ z}$
$\newcommand\BBA{\boldsymbol\RA}$
$\newcommand\BBB{\boldsymbol\RB}$
$\newcommand\BBC{\boldsymbol\RC}$
$\newcommand\BBD{\boldsymbol\RD}$
$\newcommand\BBE{\boldsymbol\RE}$
$\newcommand\BBF{\boldsymbol\RF}$
$\newcommand\BBG{\boldsymbol\RG}$
$\newcommand\BBH{\boldsymbol\RH}$
$\newcommand\BBI{\boldsymbol\RI}$
$\newcommand\BBJ{\boldsymbol\RJ}$
$\newcommand\BBK{\boldsymbol\RK}$
$\newcommand\BBL{\boldsymbol\RL}$
$\newcommand\BBM{\boldsymbol }$
$\newcommand\BBN{\boldsymbol\RN}$
$\newcommand\BBO{\boldsymbol\RO}$
$\newcommand\BBP{\boldsymbol\RP}$
$\newcommand\BBQ{\boldsymbol\RQ}$
$\newcommand\BBR{\boldsymbol\RR}$
$\newcommand\BBS{\boldsymbol\RS}$
$\newcommand\BBT{\boldsymbol\RT}$
$\newcommand\BBU{\boldsymbol\RU}$
$\newcommand\BBV{\boldsymbol\RV}$
$\newcommand\BBW{\boldsymbol\RW}$
$\newcommand\BBX{\boldsymbol\RX}$
$\newcommand\BBY{\boldsymbol\RY}$
$\newcommand\BBZ{\boldsymbol\RZ}$
$\newcommand\BBa{\boldsymbol\Ra}$
$\newcommand\BBb{\boldsymbol\Rb}$
$\newcommand\BBc{\boldsymbol\Rc}$
$\newcommand\BBd{\boldsymbol\Rd}$
$\newcommand\BBe{\boldsymbol\Re}$
$\newcommand\BBf{\boldsymbol\Rf}$
$\newcommand\BBg{\boldsymbol\Rg}$
$\newcommand\BBh{\boldsymbol\Rh}\}$
$\newcommand\BBi{\boldsymbol\Ri}$
$\newcommand\BBj{\boldsymbol\Rj}$
$\newcommand\BBk{\boldsymbol\Rk}$
$\newcommand\BBl{boldsymbol\Rl}$
$\newcommand\BBm{\boldsymbol }$
$\newcommand\BBn{\boldsymbol\Rn}$
$\newcommand\BBo{\boldsymbol\Ro}$
$\newcommand\BBp{\boldsymbol\Rp}$
$\newcommand\BBq{\boldsymbol\Rq}$
$\newcommand\BBr{\boldsymbol\Rr}$
$\newcommand\BBs{\boldsymbol\Rs}$
$\newcommand\BBt{\boldsymbol\Rt}$
$\newcommand\BBu{\boldsymbol\Ru}$
$\newcommand\BBv{\boldsymbol\Rv}$
$\newcommand\BBw{\boldsymbol\Rw}$
$\newcommand\BBx{\boldsymbol\Rx}$
$\newcommand\BBy{\boldsymbol\Ry}$
$\newcommand\BBz{\boldsymbol\Rz}$
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
$\newcommand\bnabla{\boldsymbol{\nabla}}$
$\newcommand\Bell{\boldsymbol\ell}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\newcommand\ns{^\vphantom{*}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}$
$\newcommand\izpi{\int\limits_{0}^{\infty}\!\!}$
$\newcommand\etc{\it etc.\/}$
$\newcommand\etal{\it et al.\/}$
$\newcommand\opcit{\it op. cit.\/}$
$\newcommand\ie{\it i.e.\/}$
$\newcommand\Ie{\it I.e.\/}$
$\newcommand\viz{\it viz.\/}$
$\newcommand\eg{\it e.g.\/}$
$\newcommand\Eg{\it E.g.\/}$
$\newcommand\dbar{\,{\mathchar'26\mkern-12mu d}}$
$\def\sss#1{\scriptscriptstyle #1}$
$\def\ss#1{\scriptstyle #1}$
$\def\ssr#1{\scriptstyle #1}$
$\def\ssf#1{\scriptstyle #1}$
$\newcommand\NA{N_{\ssr{\!A}}}$
$\newcommand\lala{\langle\!\langle}$
$\newcommand\rara{\rangle\!\rangle}$
$\newcommand\blan{\big\langle}$
$\newcommand\bran{\big\rangle}$
$\newcommand\Blan{\Big\langle}$
$\newcommand\Bran{\Big\rangle}$
$\newcommand\intl{\int\limits}$
$\newcommand\half{\frac{1}{2}}$
$\newcommand\third{\frac{1}{3}}$
$\newcommand\fourth{\frac{1}{4}}$
$\newcommand\eighth{\frac{1}{8}}$
$\newcommand\uar{\uparrow}$
$\newcommand\dar{\downarrow}$
$\newcommand\undertext#1{$\underline{\hbox{#1}}$}$
$\newcommand\Tra{\mathop{\textsf{Tr}}\,}$
$\newcommand\det{\mathop{\textsf{det}}\,}$
$\def\tket#1{|  #1 \rangle}$
$\def\tbra#1{\langle #1|}$
$\def\tbraket#1#2{\langle #1  |   #2 \rangle}$
$\def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}$
$\def\sket#1{|  \, #1 \,  \rangle}$
$\def\sbra#1{\langle \,  #1 \, |}$
$\def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}$
$\def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}$
$\def\ket#1{\big| \, #1\, \big\rangle}$
$\def\bra#1{\big\langle \, #1 \, \big|}$
$\def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}$
$\def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}$
$\newcommand\pz{\partial}$
$\newcommand\pzb{\bar{\partial}}$
$\newcommand\svph{\vphantom{\int}}$
$\newcommand\vph{\vphantom{\sum_i}}$
$\newcommand\bvph{\vphantom{\sum_N^N}}$
$\newcommand\nd{^{\vphantom{\dagger}}}$
$\newcommand\ns{^{\vphantom{*}}}$
$\newcommand\yd{^\dagger}$
$\newcommand\zb{\bar z}$
$\newcommand\zdot{\dot z}$
$\newcommand\zbdot{\dot{\bar z}}$
$\newcommand\kB{k_{\sss{B}}}$
$\newcommand\kT{k_{\sss{B}}T}$
$\newcommand\gtau{g_\tau}$
$\newcommand\Htil{\tilde H}$
$\newcommand\pairo{(\phi\nd_0,J\nd_0)}$
$\newcommand\pairm{(\phi\nd_0,J)}$
$\newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}$
$\newcommand\pairmb{(\Bphi\nd_0,\BJ)}$
$\newcommand\pair{(\phi,J)}$
$\newcommand\Hz{H\nd_0}$
$\newcommand\Ho{H\nd_1}$
$\newcommand\Htz{\Htil\nd_0}$
$\newcommand\Hto{\Htil\nd_1}$
$\newcommand\oc{\omega_\Rc}$

$\newcommand \gtwid{\approx}$

$\newcommand\index{\textsf{ind}}$
$\newcommand\csch{\,{ csch\,}}$
$\newcommand\ctnh{\,{ ctnh\,}}$
$\newcommand\ctn{\,{ ctn\,}}$
$\newcommand\sgn{\,{ sgn\,}}$
$\def\tmapright#1{\xrightarrow \limits^{#1}}$
$\def\bmapright#1{\xrightarrow\limits_{#1}}$
$\newcommand\hfb{\hfill\break}$
$\newcommand\Rep{\textsf{Re}\,}$
$\newcommand\Imp{\textsf{Im}\,}$
$\newcommand\ncdot{\!\cdot\!}$
$\def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }$
$\def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }$
$\newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}$

$\def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}$
$\def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}$
$\def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}$
$\def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}$
$\newcommand\subA{\ns_\ssr{A}}$
$\newcommand\subB{\ns_\ssr{B}}$
$\newcommand\subC{\ns_\ssr{C}}$
$\newcommand\subD{\ns_\ssr{D}}$
$\newcommand\subAB{\ns_\ssr{AB}}$
$\newcommand\subBC{\ns_\ssr{BC}}$
$\newcommand\subCD{\ns_\ssr{CD}}$
$\newcommand\subDA{\ns_\ssr{DA}}$
$\def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }$
$\def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}$
$\newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}$
$\newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}$
$\newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}$
$\newcommand\cds{\,\bullet\,}$
$\newcommand\ccs{\,\circ\,}$
$\newcommand\nsub{_{\vphantom{\dagger}}}$
$\newcommand\rhohat{\hat\rho}$
$\newcommand\vrhhat{\hat\vrh}$
$\newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}$
$\newcommand\brangle{\big\rangle}$
$\newcommand\blangle{\big\langle}$
$\newcommand\vet{\tilde\ve}$
$\newcommand\zbar{\bar z}$
$\newcommand\ftil{\tilde f}$
$\newcommand\XBE{\RXi\ns_\ssr{BE}}$
$\newcommand\XFD{\RXi\ns_\ssr{FD}}$
$\newcommand\OBE{\Omega\ns_\ssr{BE}}$
$\newcommand\OFD{\Omega\ns_\ssr{FD}}$
$\newcommand\veF{\ve\ns_\RF}$
$\newcommand\kF{k\ns_\RF}$
$\newcommand\kFu{k\ns_{\RF\uar}}$
$\newcommand\SZ{\textsf Z}}$ \( \newcommand\kFd{k\ns_{\RF\dar}\)
$\newcommand\muB{\mu\ns_\ssr{B}}$
$\newcommand\mutB{\tilde\mu}\ns_\ssr{B}$
$\newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}$
$\newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}$
$\newcommand\xhiOZ{\xhi^\ssr{OZ}}$
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\jhz{\HJ(0)}$
$\newcommand\nda{\nd_\alpha}$
$\newcommand\ndap{\nd_{\alpha'}}$
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/03:_Ergodicity_and_the_Approach_to_Equilibrium/3.03:_Irreversibility_and_Poincare_Recurrence), /content/body/p[1]/span, line 1, column 23

\)
$\newcommand\msa{m\ns_\ssr{A}}$
$\newcommand\msb{m\ns_\ssr{B}}$
$\newcommand\mss{m\ns_\Rs}$
$\newcommand\HBx{\hat\Bx}$
$\newcommand\HBy{\hat\By}$
$\newcommand\HBz{\hat\Bz}$
$\newcommand\thm{\theta\ns_m}$
$\newcommand\thp{\theta\ns_\phi}$
$\newcommand\mtil{\widetilde m}$
$\newcommand\phitil{\widetilde\phi}$
$\newcommand\delf{\delta\! f}$
$\newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}$
$\newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}$
$\newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}$
$\newcommand\vbar{\bar v}$
$\newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}$
$\newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}$
$\newcommand\gla{g\nd_{\RLambda\nd}}$
$\newcommand\TA{T\ns_\ssr{A}}$
$\newcommand\TB{T\ns_\ssr{B}}$
$\newcommand\ncdot{\!\cdot\!}$
$\newcommand\NS{N\ns_{\textsf S}}$

The dynamics of the master equation describe an approach to equilibrium. These dynamics are irreversible: $d\SH/dt \le 0$, where $\SH$ is Boltzmann’s $\SH$-function. However, the microscopic laws of physics are (almost) time-reversal invariant⁴, so how can we understand the emergence of irreversibility? Furthermore, any dynamics which are deterministic and volume-preserving in a finite phase space exhibits the phenomenon of Poincaré recurrence, which guarantees that phase space trajectories are arbitrarily close to periodic if one waits long enough.

Poincaré Recurrence Theorem

The proof of the recurrence theorem is simple. Let $\gtau$ be the ‘$\tau$-advance mapping’ which evolves points in phase space according to Hamilton’s equations. Assume that $\gtau$ is invertible and volume-preserving, as is the case for Hamiltonian flow. Further assume that phase space volume is finite. Since energy is preserved in the case of time-independent Hamiltonians, we simply ask that the volume of phase space at fixed total energy $E$ be finite,

$$\int\!\!d\mu\,\delta\big(E-H(\Bq,\Bp)\big) < \infty\ ,$$

where $d\mu=d\Bq\,d\Bp$ is the phase space uniform integration measure.

In any finite neighborhood $\CR\ns_0$ of phase space there exists a point $\Bvphi\nd_0$ which will return to $\CR\ns_0$ after $m$ applications of $\gtau$, where $m$ is finite.

Figure $\PageIndex{1}$: Successive images of a set $\CR_0$ under the $\tau$-advance mapping $g_\tau$, projected onto a two-dimensional phase plane. The Poincaré recurrence theorem guarantees that if phase space has finite volume, and $g_\tau$ is invertible and volume preserving, then for any set $\CR_0$ there exists an integer $m$ such that $\CR_0\cap g_\tau^m\,\CR_0\ne\emptyset$.

Assume the theorem fails; we will show this assumption results in a contradiction. Consider the set $\RUps$ formed from the union of all sets $\gtau^k\,\CR$ for all $m$:

$$\RUps=\bigcup_{k=0}^\infty \gtau^k\,\CR\ns_0$$

We assume that the set $\{\gtau^k\,\CR\ns_0\, | \, k\!\in \MN\}$ is disjoint⁵. The volume of a union of disjoint sets is the sum of the individual volumes. Thus,

$$\begin{split} {vol}(\RUps)&=\sum_{k=0}^\infty{vol}\big(\gtau^k\,\CR\ns_0\big)\\ &={vol}(\CR\ns_0)\cdot\sum_{k=0}^\infty 1 = \infty\ , \end{split}$$

since ${vol}\big(\gtau^k\,\CR\ns_0\big)={vol}\big(\CR\ns_0\big)$ from volume preservation. But clearly $\RUps$ is a subset of the entire phase space, hence we have a contradiction, because by assumption phase space is of finite volume.

Thus, the assumption that the set $\{\gtau^k\,\CR\ns_0\, | \, k\!\in\! \MZ\ns_+\}$ is disjoint fails. This means that there exists some pair of integers $k$ and $l$, with $k\ne l$, such that $\gtau^k\,\CR\ns_0\cap \gtau^l\,\CR\ns_0\ne\emptyset$. Without loss of generality we may assume $k<l$. Apply the inverse $\gtau^{-1}$ to this relation $k$ times to get $\gtau^{l-k}\,\CR\ns_0\cap \CR\ns_0\ne\emptyset$. Now choose any point $\Bvphi\ns_1\in\gtau^m\,\CR\ns_0\cap \CR\ns_0$, where $m=l-k$, and define $\Bvphi\nd_0=\gtau^{-m}\Bvphi\ns_1$. Then by construction both $\Bvphi\nd_0$ and $\gtau^m\,\Bvphi\nd_0$ lie within $\CR\ns_0$ and the theorem is proven.

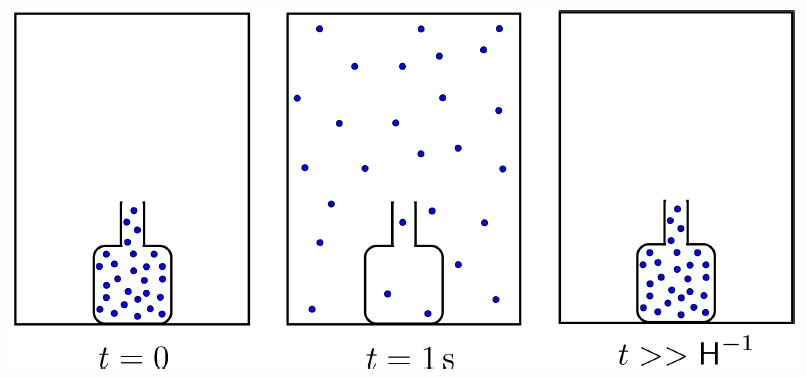
Poincaré recurrence has remarkable implications. Consider a bottle of perfume which is opened in an otherwise evacuated room, as depicted in Figure $\PageIndex{2}$. The perfume molecules evolve according to Hamiltonian evolution. The positions are bounded because physical space is finite. The momenta are bounded because the total energy is conserved, hence no single particle can have a momentum such that $T(\Bp)>E\ns_{\ssr{TOT}}$, where $T(\Bp)$ is the single particle kinetic energy function⁶. Thus, phase space, however large, is still bounded. Hamiltonian evolution, as we have seen, is invertible and volume preserving, therefore the system is recurrent. All the molecules must eventually return to the bottle. What’s more, they all must return with momenta arbitrarily close to their initial momenta!⁷ In this case, we could define the region $\CR\ns_0$ as

$$\CR\ns_0=\big\{ (q\ns_1,\ldots,q\ns_r,p\ns_1,\ldots,p\ns_r)\ \big|\ |q\ns_i-q^0_i| \le\RDelta q \ {and}\ |p\ns_j-p^0_j| \le\RDelta p\ \forall\ i,j\big\}\ ,$$

which specifies a hypercube in phase space centered about the point $(\Bq^0,\Bp^0)$.

Figure $\PageIndex{2}$: Poincaré recurrence guarantees that if we remove the cap from a bottle of perfume in an otherwise evacuated room, all the perfume molecules will eventually return to the bottle! (Here $\SH$ is the Hubble constant.)

Each of the three central assumptions – finite phase space, invertibility, and volume preservation – is crucial. If any one of these assumptions does not hold, the proof fails. Obviously if phase space is infinite the flow needn’t be recurrent since it can keep moving off in a particular direction. Consider next a volume-preserving map which is not invertible. An example might be a mapping $f\colon\MR\to\MR$ which takes any real number to its fractional part. Thus, $f(\pi)=0.14159265\ldots$. Let us restrict our attention to intervals of width less than unity. Clearly $f$ is then volume preserving. The action of $f$ on the interval $[2,3)$ is to map it to the interval $[0,1)$. But $[0,1)$ remains fixed under the action of $f$, so no point within the interval $[2,3)$ will ever return under repeated iterations of $f$. Thus, $f$ does not exhibit Poincaré recurrence.

Consider next the case of the damped harmonic oscillator. In this case, phase space volumes contract. For a one-dimensional oscillator obeying ${\ddot x} + 2\beta{\dot x} + \Omega_0^2\, x=0$ one has $\nabla\!\cdot\!\BV=-2\beta<0$, since $\beta>0$ for physical damping. Thus the convective derivative is $D_t\vrh=-(\nabla\!\cdot \!\BV)\vrh=2\beta\vrh$ which says that the density increases exponentially in the comoving frame, as $\vrh(t)=e^{2\beta t}\, \vrh(0)$. Thus, phase space volumes collapse: $\ROmega(t)=e^{-2\beta 2}\,\ROmega(0)$, and are not preserved by the dynamics. The proof of recurrence therefore fails. In this case, it is possible for the set $\RUps$ to be of finite volume, even if it is the union of an infinite number of sets $\gtau^k\,\CR\ns_0$, because the volumes of these component sets themselves decrease exponentially, as ${vol}(\gtau^n\,\CR\ns_0)=e^{-2n\beta\tau}\, {vol}(\CR\ns_0)$. A damped pendulum, released from rest at some small angle $\theta\nd_0$, will not return arbitrarily close to these initial conditions.

Kac ring model

The implications of the Poincaré recurrence theorem are surprising – even shocking. If one takes a bottle of perfume in a sealed, evacuated room and opens it, the perfume molecules will diffuse throughout the room. The recurrence theorem guarantees that after some finite time $T$ all the molecules will go back inside the bottle (and arbitrarily close to their initial velocities as well). The hitch is that this could take a very long time, much much longer than the age of the Universe.

On less absurd time scales, we know that most systems come to thermodynamic equilibrium. But how can a system both exhibit equilibration and Poincaré recurrence? The two concepts seem utterly incompatible!

A beautifully simple model due to Kac shows how a recurrent system can exhibit the phenomenon of equilibration. Consider a ring with $N$ sites. On each site, place a ‘spin’ which can be in one of two states: up or down. Along the $N$ links of the system, $F$ of them contain ‘flippers’. The configuration of the flippers is set at the outset and never changes. The dynamics of the system are as follows: during each time step, every spin moves clockwise a distance of one lattice spacing. Spins which pass through flippers reverse their orientation: up becomes down, and down becomes up.

Figure $\PageIndex{3}$: Left: A configuration of the Kac ring with $N=16$ sites and $F=4$ flippers. The flippers, which live on the links, are represented by blue dots. Right: The ring system after one time step. Evolution proceeds by clockwise rotation. Spins passing through flippers are flipped.

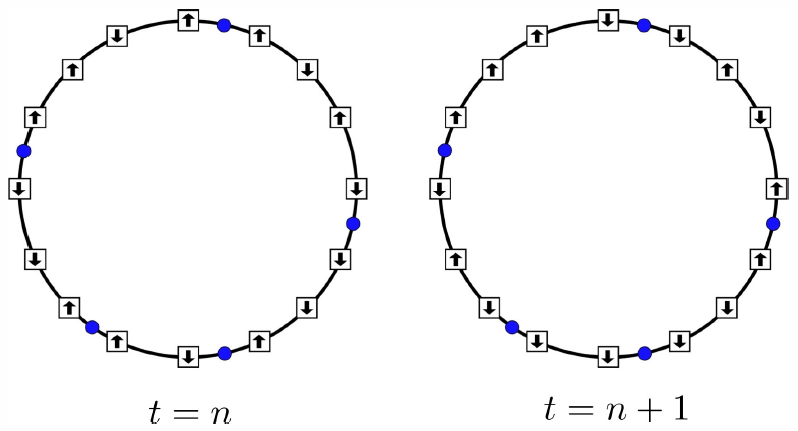
The ‘phase space’ for this system consists of $2^N$ discrete configurations. Since each configuration maps onto a unique image under the evolution of the system, phase space ‘volume’ is preserved. The evolution is invertible; the inverse is obtained simply by rotating the spins counterclockwise. Figure $\PageIndex{3}$ depicts an example configuration for the system, and its first iteration under the dynamics.

Figure $\PageIndex{4}$: Three simulations of the Kac ring model with $N=2500$ sites and three different concentrations of flippers. The red line shows the magnetization as a function of time, starting from an initial configuration in which 100% of the spins are up. The blue line shows the prediction of the Stosszahlansatz, which yields an exponentially decaying magnetization with time constant $\tau$.

Suppose the flippers were not fixed, but moved about randomly. In this case, we could focus on a single spin and determine its configuration probabilistically. Let $p_n$ be the probability that a given spin is in the up configuration at time $n$. The probability that it is up at time $(n+1)$ is then

$$p_{n+1}=(1-x)\,p_n + x\,(1-p_n)\ ,\label{stoss}$$

where $x=F/N$ is the fraction of flippers in the system. In words: a spin will be up at time $(n+1)$ if it was up at time $n$ and did not pass through a flipper, or if it was down at time $n$ and did pass through a flipper. If the flipper locations are randomized at each time step, then the probability of flipping is simply $x=F/N$. Equation $\ref{stoss}$ can be solved immediately:

$$p_n=\half+(1-2x)^n\,(p_0-\half)\ ,$$

which decays exponentially to the equilibrium value of $p\nd_{eq}=\half$ with time scale

$$\tau(x)=-{1\over \ln|1-2x|}\ .$$

We identify $\tau(x)$ as the microscopic relaxation time over which local equilibrium is established. If we define the magnetization $m\equiv (N\nd_\uar-N\nd_\dar)/N$, then $m=2p-1$, so $m_n=(1-2x)^n\,m_0$. The equilibrium magnetization is $m\nd_{eq}=0$. Note that for $\half < x < 1$ that the magnetization reverses sign each time step, as well as decreasing exponentially in magnitude.

Figure $\PageIndex{5}$: Simulations of the Kac ring model. Top: $N=2500$ sites with $F=201$ flippers. After $2500$ iterations, each spin has flipped an odd number of times, so the recurrence time is $2N$. Middle: $N=2500$ with $F=2400$, resulting in a near-complete reversal of the population with every iteration. Bottom: $N=25000$ with $N=1000$, showing long time equilibration and dramatic resurgence of the spin population.

The assumption that leads to equation $\ref{stoss}$ is called the Stosszahlansatz⁸, a long German word meaning, approximately, ‘assumption on the counting of hits’. The resulting dynamics are irreversible: the magnetization inexorably decays to zero. However, the Kac ring model is purely deterministic, and the Stosszahlansatz can at best be an approximation to the true dynamics. Clearly the Stosszahlansatz fails to account for correlations such as the following: if spin $i$ is flipped at time $n$, then spin $i+1$ will have been flipped at time $n-1$. Also if spin $i$ is flipped at time $n$, then it also will be flipped at time $n+N$. Indeed, since the dynamics of the Kac ring model are invertible and volume preserving, it must exhibit Poincaré recurrence. We see this most vividly in Figures $\PageIndex{4}$ and $\PageIndex{5}$.

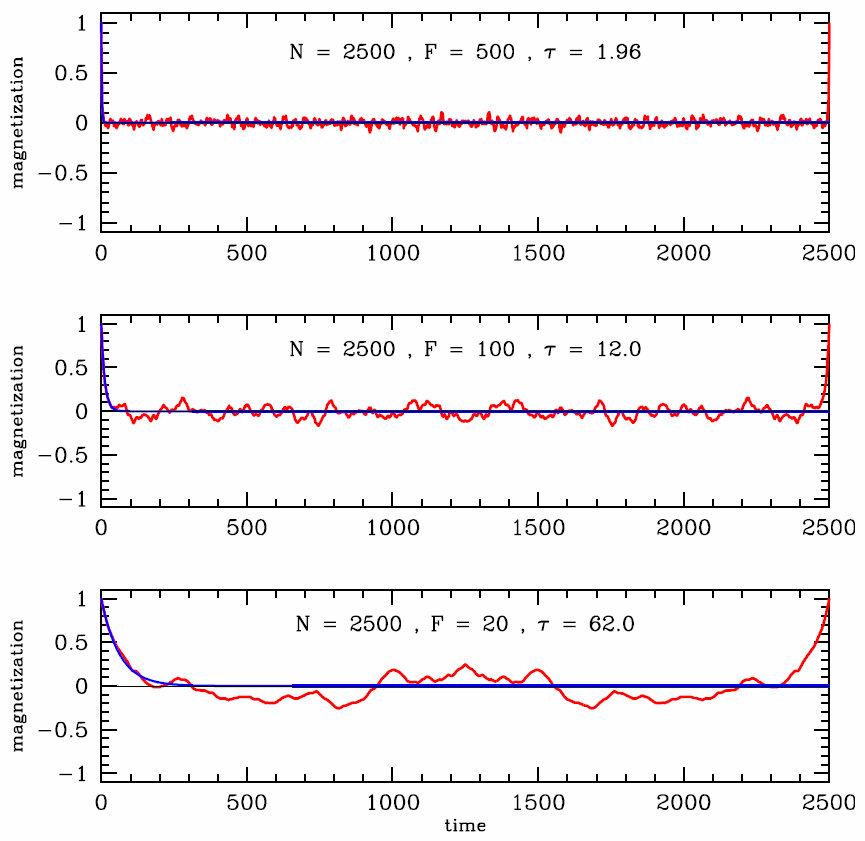
The model is trivial to simulate. The results of such a simulation are shown in Figure $\PageIndex{4}$ for a ring of $N=1000$ sites, with $F=100$ and $F=24$ flippers. Note how the magnetization decays and fluctuates about the equilibrium value $m\nd_{eq}=0$, but that after $N$ iterations $m$ recovers its initial value: $m\nd_N=m\nd_0$. The recurrence time for this system is simply $N$ if $F$ is even, and $2N$ if $F$ is odd, since every spin will then have flipped an even number of times.

In Figure $\PageIndex{5}$ we plot two other simulations. The top panel shows what happens when $x>\half$, so that the magnetization wants to reverse its sign with every iteration. The bottom panel shows a simulation for a larger ring, with $N=25000$ sites. Note that the fluctuations in $m$ about equilibrium are smaller than in the cases with $N=1000$ sites. Why?