7.1: The van der Waals system
( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand\Dalpha
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dbeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dgamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Ddelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Depsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarepsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dzeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Deta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dtheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dvartheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Diota
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dkappa
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dlambda
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\DGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\DDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\DTheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vmu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vnu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vxi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vom
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vtau
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vupsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vchi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vpsi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\Vomega
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\VGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\VDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\newcommand\BI{\mib I}}
\)
\newcommand { M}
\newcommand { m}
}
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
1$#1_$
\newcommand\SZ{\textsf Z}} \( \newcommand\kFd{k\ns_{\RF\dar}\)
\newcommand\mutB{\tilde\mu}\ns_\ssr{B}
\( \newcommand\xhihOZ
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
\( \newcommand\labar
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23
Equation of state
Recall the van der Waals equation of state,
(p+av2)(v−b)=RT ,
where v=N∗AV/N is the molar volume. Solving for p(v,T), we have
p=RTv−b−av2.
Let us fix the temperature T and examine the function p(v). Clearly p(v) is a decreasing function of volume for v just above the minimum allowed value v=b, as well as for v→∞. But is p(v) a monotonic function for all v∈[b,∞]?
We can answer this by computing the derivative,
(∂p∂v)∗T=2av3−RT(v−b)2.
Setting this expression to zero for finite v, we obtain the equation1
2abRT=u3(u−1)2 ,
where u≡v/b is dimensionless. It is easy to see that the function f(u)=u3/(u−1)2 has a unique minimum for u>1. Setting f′(u∗)=0 yields u∗=3, and so f∗min=f(3)=274. Thus, for T>T∗c=8a/27bR, the LHS of Equation ??? lies below the minimum value of the RHS, and there is no solution. This means that p(v,T>T∗c) is a monotonically decreasing function of v.
At T=T∗c there is a saddle-node bifurcation. Setting v∗c=bu∗=3b and evaluating p∗c=p(v∗c,T∗c), we have that the location of the critical point for the van der Waals system is
p∗c=a27b2,v∗c=3b,T∗c=8a27bR.
For T<T∗c, there are two solutions to Equation ???, corresponding to a local minimum and a local maximum of the function p(v). The locus of points in the (v,p) plane for which (∂p/∂v)∗T=0 is obtained by setting Equation ??? to zero and solving for T, then substituting this into Equation ???. The result is
p∗(v)=av2−2abv3.
Expressed in terms of dimensionless quantities ˉp=p/p∗c and ˉv=v/v∗c, this equation becomes
ˉp∗(ˉv)=3ˉv2−2ˉv3.
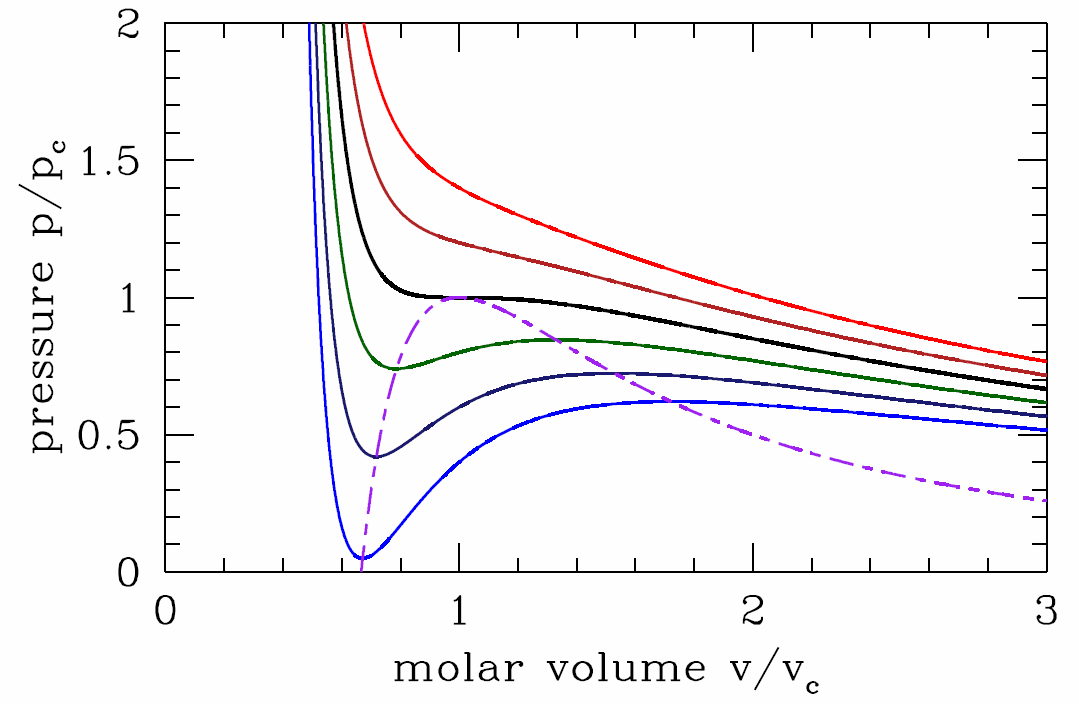
Along the curve p=p∗(v), the isothermal compressibility, κ∗T=−1v(∂v∂p)∗T diverges, heralding a thermodynamic instability. To understand better, let us compute the free energy of the van der Waals system, F=E−TS. Regarding the energy E, we showed back in chapter 2 that
(∂ε∂v)∗T=T(∂p∂T)∗V−p=av2 ,
which entails
ε(T,v)=12fRT−av ,
where ε=E/ν is the molar internal energy. The first term is the molar energy of an ideal gas, where f is the number of molecular freedoms, which is the appropriate low density limit. The molar specific heat is then c∗V=(∂ε∂T)∗v=f2R, which means that the molar entropy is
s(T,v)=∫TdT′ c∗VT′=f2Rln(T/T∗c)+s∗1(v) .
We then write f=ε−Ts, and we fix the function s∗1(v) by demanding that p=−(∂f∂v)∗T . This yields s∗1(v)=Rln(v−b)+s∗0, where s∗0 is a constant. Thus2,
f(T,v)=f2RT(1−ln(T/T∗c))−av−RTln(v−b)−Ts∗0 .
| gas | a (L2⋅barmol2) | b (Lmol) | p∗c (bar) | T∗c (K) | v∗c ( L/mol) |
|---|---|---|---|---|---|
| Acetone | 14.09 | 0.0994 | 52.82 | 505.1 | 0.2982 |
| Argon | 1.363 | 0.03219 | 48.72 | 150.9 | 0.0966 |
| Carbon dioxide | 3.640 | 0.04267 | 7404 | 304.0 | 0.1280 |
| Ethanol | 12.18 | 0.08407 | 63.83 | 516.3 | 0.2522 |
| Freon | 10.78 | 0.0998 | 40.09 | 384.9 | 0.2994 |
| Helium | 0.03457 | 0.0237 | 2.279 | 5.198 | 0.0711 |
| Hydrogen | 0.2476 | 0.02661 | 12.95 | 33.16 | 0.0798 |
| Mercury | 8.200 | 0.01696 | 1055 | 1723 | 0.0509 |
| Methane | 2.283 | 0.04278 | 46.20 | 190.2 | 0.1283 |
| Nitrogen | 1.408 | 0.03913 | 34.06 | 128.2 | 0.1174 |
| Oxygen | 1.378 | 0.03183 | 50.37 | 154.3 | 0.0955 |
| Water | 5.536 | 0.03049 | 220.6 | 647.0 | 0.0915 |
We know that under equilibrium conditions, f is driven to a minimum by spontaneous processes. Now suppose that ∂2f∂v2|†T<0 over some range of v at a given temperature T. This would mean that one mole of the system at volume v and temperature T could lower its energy by rearranging into two half-moles, with respective molar volumes v±δv, each at temperature T. The total volume and temperature thus remain fixed, but the free energy changes by an amount Δf=12∂2f∂v2|†T(δv)2<0. This means that the system is unstable – it can lower its energy by dividing up into two subsystems each with different densities ( molar volumes). Note that the onset of stability occurs when
∂2f∂v2|†T=−∂p∂v|†T=1vκ∗p=0 ,
which is to say when κ∗p=∞. As we saw, this occurs at p=p∗(v), given in Equation [pstar].
However, this condition, ∂2f∂v2|†T<0, is in fact too strong. That is, the system can be unstable even at molar volumes where ∂2f∂v2|†T>0. The reason is shown graphically in Figure 7.1.2. At the fixed temperature T, for any molar volume v between v∗liquid≡v∗1 and v∗gas≡v∗2, the system can lower its free energy by phase separating into regions of different molar volumes. In general we can write
v=(1−x)v∗1+xv∗2 ,
so v=v∗1 when x=0 and v=v∗2 when x=1. The free energy upon phase separation is simply
f=(1−x)f∗1+xf∗2 ,
where f∗j=f(v∗j,T). This function is given by the straight black line connecting the points at volumes v∗1 and v∗2 in Figure 7.1.2.
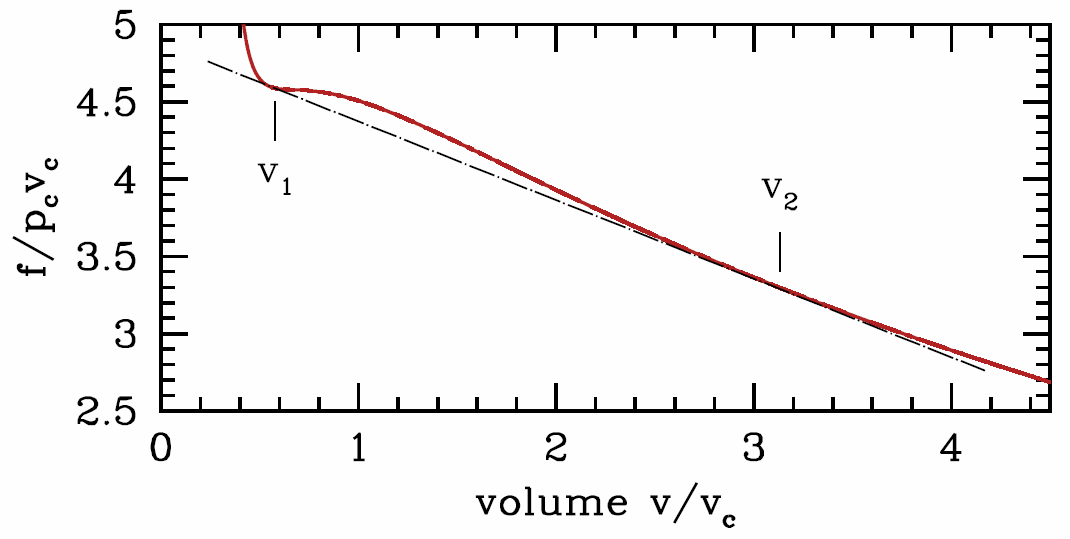
The two equations which give us v∗1 and v∗2 are
∂f∂v|†v∗1,T= ∂f∂v|†v∗2,T=f(T,v∗2)−f(T,v∗1)(v∗2−v∗1).
Equivalently, in terms of the pressure, p=−∂f∂v|†T , these equations are equivalent to
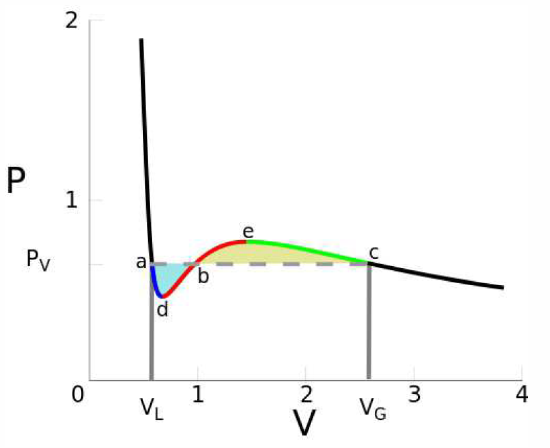
p(T,v∗1)=p(T,v∗2)=1v∗2−v∗1v∗2∫v∗1dvp(T,v).
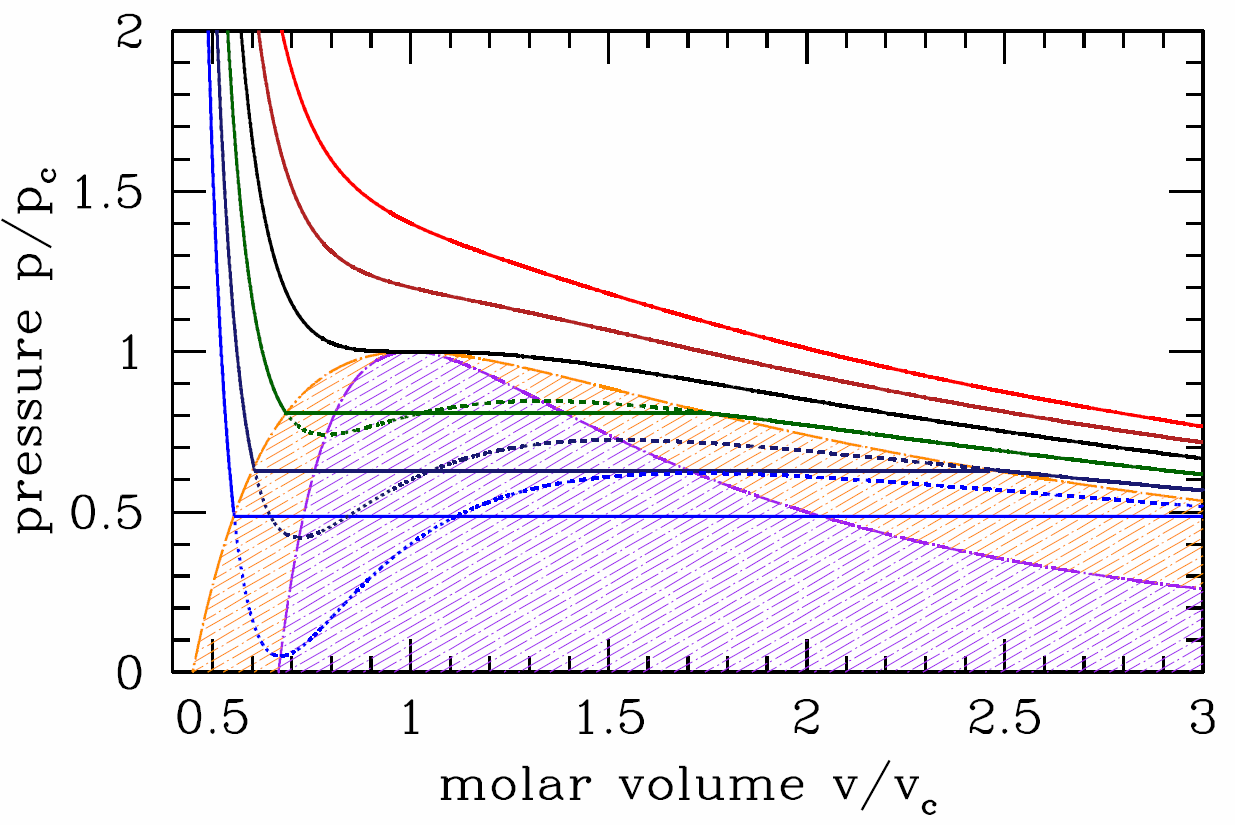
This procedure is known as the Maxwell construction, and is depicted graphically in Figure 7.1.3. When the Maxwell construction is enforced, the isotherms resemble the curves in Figure 7.1.1. In this figure, all points within the purple shaded region have ∂2f∂v2<0, hence this region is unstable to infinitesimal fluctuations. The boundary of this region is called the spinodal, and the spontaneous phase separation into two phases is a process known as spinodal decomposition. The dot-dashed orange curve, called the coexistence curve, marks the instability boundary for nucleation. In a nucleation process, an energy barrier must be overcome in order to achieve the lower free energy state. There is no energy barrier for spinodal decomposition – it is a spontaneous process.
Analytic form of the coexistence curve near the critical point
We write v∗L=v∗c+w∗L and v∗G=v∗c+w∗G. One of our equations is p(v∗c+w∗L,T)=p(v∗c+w∗G,T). Taylor expanding in powers of w∗L and w∗G , we have
0=p∗v(v∗c,T)(w∗G−w∗L)+12p∗vv(v∗c,T)(w2G−w2L)+16p∗vvv(v∗c,T)(w3G−w3L)+… ,
where
p∗v≡∂p∂v,p∗vv≡∂2p∂v2,p∗vvv≡∂3p∂v3,p∗vT≡∂2p∂v∂T,etc.
The second equation we write as
w∗G∫w∗Ldwp(v∗c+w,T)=12(w∗G−w∗L)(p(v∗c+w∗L,T)+p(v∗c+w∗G,T)) .
Expanding in powers of w∗L and w∗G, this becomes
p(v∗c,T)(w∗G−w∗L)+12p∗v(v∗c,T)(w2G−w2L)+16p∗vv(v∗c,T)(w3G−w3L)+124p∗vvv(v∗c,T)(w4G−w4L)+1120p∗vvvv(v∗c,T)(w5G−w5L)+…=12(w∗G−w∗L){2p(v∗c,T)+p∗v(v∗c,T)(w∗G+w∗L)+12p∗vv(v∗c,T)(w2G+w2L)+16p∗vvv(v∗c,T)(w3G+w3L)+124p∗vvvv(v∗c,T)(w4G+w4L)+…}
Subtracting the LHS from the RHS, we find that we can then divide by 16(w2G−w2L), resulting in
0=p∗vv(v∗c,T)+12p∗vvv(v∗c,T)(w∗G+w∗L)+120p∗vvvv(v∗c,T)(3w2G+4w∗Gw∗L+3w2L)+O(w3G,L) .
We now define w∗±≡w∗G±w∗L. In terms of these variables, Equations ??? and ??? become
0=p∗v(v∗c,T)+12p∗vv(v∗c,T)w∗++18p∗vvv(v∗c,T)(w2++13w2−)+O(w3±)∑i0=p∗vv(v∗c,T)+12p∗vvv(v∗c,T)w∗++18p∗vvvv(v∗c,T)(w2++15w2−)+O(w3±) .
We now evaluate w∗± to order T. Note that p∗v(v∗c,T∗c)=p∗vv(v∗c,T∗c)=0, since the critical point is an inflection point in the (v,p) plane. Thus, we have p∗v(v∗c,T)=p∗vTΘ+O(Θ2), where T=T∗c+Θ and p∗vT=p∗vT(v∗c,T∗c). We can then see that w∗− is of leading order √−Θ, while w∗+ is of leading order Θ. This allows us to write
0=p∗vTΘ+124p∗vvvw2−+O(Θ2)∑i0=p∗vvTΘ+12p∗vvvw∗++140p∗vvvvw2−+O(Θ2) .
Thus,
w∗−=(24p∗vTpvvv)1/2√−Θ+…∑iw∗+=(6p∗vTp∗vvvv−10p∗vvvp∗vvT5p2vvv)Θ+… .
We then have
w∗L=−(6p∗vTpvvv)1/2√−Θ+(3p∗vTp∗vvvv−5p∗vvvp∗vvT5p2vvv)Θ+O(Θ3/2)∑iw∗G=(6p∗vTpvvv)1/2√−Θ+(3p∗vTp∗vvvv−5p∗vvvp∗vvT5p2vvv)Θ+O(Θ3/2) .
Suppose we follow along an isotherm starting from the high molar volume (gas) phase. If T>T∗c, the volume v decreases continuously as the pressure p increases. If T<T∗c, then at the instant the isotherm first intersects the orange boundary curve in Figure 7.1.4, there is a discontinuous change in the molar volume from high (gas) to low (liquid). This discontinuous change is the hallmark of a first order phase transition. Note that the volume discontinuity, Δv=w∗−∝(T∗c−T)1/2. This is an example of a critical behavior in which the order parameter ϕ, which in this case may be taken to be the difference ϕ=v∗G−v∗L, behaves as a power law in |T−T∗c|, where T∗c is the critical temperature. In this case, we have ϕ(T)∝(T∗c−T)β+, where β=12 is the exponent, and where (T∗c−T)+ is defined to be T∗c−T if T<T∗c and 0 otherwise. The isothermal compressibility is κ∗T=−v/p∗v(v,T). This is finite along the coexistence curve – it diverges only along the spinodal. It therefore diverges at the critical point, which lies at the intersection of the spinodal and the coexistence curve.
It is convenient to express the equation of state and the coexistence curve in terms of dimensionless variables. Write
ˉp=pp∗c,ˉv=vv∗c,ˉT=TT∗c.
The van der Waals equation of state then becomes
ˉp=8ˉT3ˉv−1−3ˉv2 .
Further expressing these dimensionless quantities in terms of distance from the critical point, we write
ˉp=1+π,ˉv=1+ϵ,ˉT=1+t .
Thus,
π(ϵ,t)=8(1+t)2+3ϵ−3(1+ϵ)2−1 .
Note that the LHS and the RHS of this equation vanish identically for (π,ϵ,t)=(0,0,0). We can then write
ϵ∗L,G=∓(6π∗ϵtπ∗ϵϵϵ)1/2(−t)1/2+(3π∗ϵtπ∗ϵϵϵϵ−5π∗ϵϵϵπ∗ϵϵt5π2ϵϵϵ)t+O((−t)3/2) .
History of the van der Waals equation
The van der Waals equation of state first appears in van der Waals’ 1873 PhD thesis3, “Over de Continuïteit van den Gas - en Vloeistoftoestand” (“On the continuity of the gas and liquid state”). In his Nobel lecture4, van der Waals writes of how he was inspired by Rudolf Clausius’ 1857 treatise on the nature of heat, where it is posited that a gas in fact consists of microscopic particles whizzing around at high velocities. van der Waals reasoned that liquids, which result when gases are compressed, also consist of ’small moving particles’: "Thus I conceived the idea that there is no essential difference between the gaseous and the liquid state of matter…"
Clausius’ treatise showed how his kinetic theory of heat was consistent with Boyle’s law for gases ( pV=constant at fixed temperature). van der Waals pondered why this might fail for the non-dilute liquid phase, and he reasoned that there were two principal differences: inter-particle attraction and excluded volume. These considerations prompted him to posit his famous equation,
p=RTv−b−av2.
The first term on the RHS accounts for excluded volume effects, and the second for mutual attractions.
In the limiting case of p→∞, the molar volume approaches v=b. On physical grounds, one might expect b=v∗0/ζ, where v∗0=NAω∗0 is NA times the volume ω∗0 of a single molecule, and the packing fraction is ζ=Nω∗0/V=v∗0/v, which is the ratio of the total molecular volume to the total system volume. In three dimensions, the maximum possible packing fraction is for fcc and hcp lattices, each of which have coordination number 12, with ζ∗max=π3√2=0.74078. Dense random packing results in ζ∗drp=0.634. Expanding the vdW equation of state in inverse powers of v yields
p=RTv+(b−aRT)⋅RTv2+O(v−3) ,
and we read of the second virial coefficient B∗2=(b−aRT)/NA. For hard spheres, a=0, and the result B∗2=4ω∗0 from the Mayer cluster expansion corresponds to b∗Mayer=4v∗0 , which is larger than the result from even the loosest regular sphere packing, that for a cubic lattice, with ζ∗cub=π6.
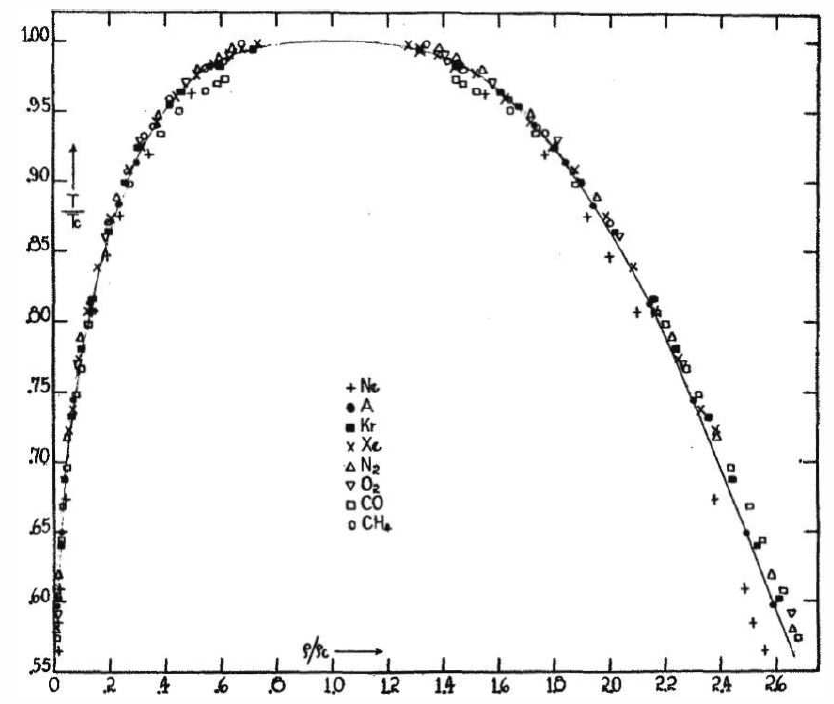
Another of van der Waals’ great achievements was his articulation of the law of corresponding states. Recall that the van der Waals equation of state, when written in terms of dimensionless quantities ˉp=p/p∗c , ˉv=v/v∗c , and ˉT=T/T∗c, takes the form of Equation ???. Thus, while the a and b parameters are specific to each fluid – see Table 7.1.1 – when written in terms of these scaled dimensionless variables, the equation of state and all its consequent properties ( the liquid-gas phase transition) are universal.
The van der Waals equation is best viewed as semi-phenomenological. Interaction and excluded volume effects surely are present, but the van der Waals equation itself only captures them in a very approximate way. It is applicable to gases, where it successfully predicts features that are not present in ideal systems ( throttling). It is of only qualitative and pedagogical use in the study of fluids, the essential physics of which lies in the behavior of quantities like the pair distribution function g(r). As we saw in chapter 6, any adequate first principles derivation of g(r) - a function which can be measured in scattering experiments - involves rather complicated approximation schemes to close the BBGKY hierarchy. Else one must resort to numerical simulations such as the Monte Carlo method. Nevertheless, the lessons learned from the van der Waals system are invaluable and they provide us with a first glimpse of what is going on in the vicinity of a phase transition, and how nonanalytic behavior, such as v∗G−v∗L∝(T∗c−T)β with noninteger exponent β may result due to singularities in the free energy at the critical point.


