1.2: Heat and Temperature
- Page ID
- 2866
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Temperature is a macroscopic measurement
Scientists have been using concepts of temperature, heat, thermal energy, and entropy to describe systems since long before it was accepted that systems are comprised of atoms and molecules. For example, people have recognized temperature since before the word temperature existed, since we can directly detect an object's temperature by touching it. We also know from experience that when a cold object is touched to a hot object, "something" will seemingly flow from the hot object to the cold object, such that the two are eventually at the same temperature.
Temperature, heat, thermal energy, and entropy are all what we call macroscopic measurements. That is, they can be used to describe large systems with many particles, but it is not necessary to know that the objects are made of particles to take these measurements. This makes them very useful for describing overall changes in a system. Measuring any of these is typically a simple process, since no knowledge of the system's microscopic configuration is needed.
The study of how a macroscopic system's temperature, thermal energy, entropy, and other macroscopic measurements change through interactions is called thermodynamics, which is the main focus of this class. Thermodynamics became a well developed field during the 1800's. It is no coincidence that the first steam engines, refrigerators, and combustion engines were built during that time. The investigation of thermodynamics is perhaps the most useful field of physics, after only electronics.
In the early 1900's, thermodynamics was built upon in an astounding way: the macroscopic measurements, which seemingly can be defined independently of our knowledge of particles, become deeply connected with the microscopic state of a system. This was called statistical mechanics, a theory which is able to explain the macroscopic characteristics of a system by studying the statistical behavior of its particles. If there is time, this will hopefully be touched on at the end of the course. For now, let's talk about the most "basic" macroscopic measurement, temperature.
The Prototypical Thermal Process
To ask the right question is harder than to answer it. -George Cantor
To ask the right questions about temperature and heat, consider the following commonplace situation. A hot block of metal is dropped into a cold beaker of water. We know from experience that the block will become cooler while the water becomes warmer, until they reach the same temperature, at which point the process seems to be over in some sense — that is, without outside interference, the block and the water will stay at this new "warm" temperature forever. This point is called thermal equilibrium, and is the key to understanding temperature.
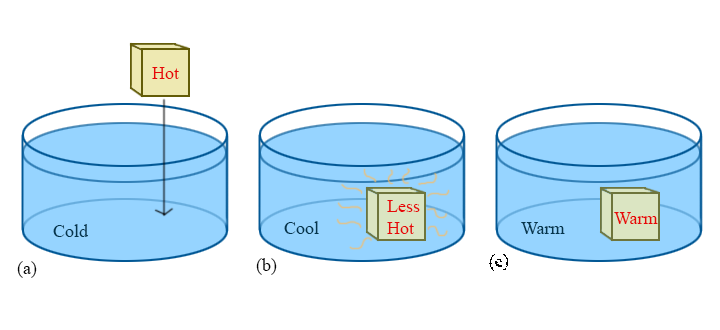
Now we naively ask:
- What is temperature, really? What is happening in these objects when they become "hotter" or "colder"? What is the relationship between temperature, heat, and thermal energy?
- What exactly is meant by heat? There is a vague idea that heat is responsible for temperature, or that heat is what flows from one object to another when they approach thermal equilibrium, but how would a physicist define it?
- What causes systems to reach thermal equilibrium? Why does heat flow between objects of different temperature? Why does it stop once it reaches a certain point? What is the significance of temperature in this process?
- Why does heat never flow from cold to hot? What is so special about the hot to cold direction?
To answer these questions fully will take the remainder of this course. For this reason, this simple hot-to-cold process will be referenced throughout the discussion of thermodynamics. It may seem trivial, or even boring, but there is a lot to be learned from this simple example and the questions that come with it.
A Starting Point
The first statement we can make, without making any quantitative claims, is a way of pinning down what temperature is all about, in terms of thermal equilibrium. This is often called the zeroth law of thermodynamics.
Temperature and Thermal Equilibrium
The zeroth law of thermodynamics states that if two thermodynamic systems are each in thermal equilibrium with a third, then they must be in thermal equilibrium with each other as well.
This is the foundation of why a thermometer is a valid way to measure temperature: it essentially states that thermometers will agree with other thermometers. Stated another way, with the validity of temperature in mind, the law can be read like this:
Temperature is a well-defined measurement of a system such that two objects in thermal contact are in equilibrium if and only if they they both have the same temperature.
These should not sound particularly profound. After a little interpretation, you should read this law as saying something like this:
"Objects with the same temperature are in thermal equilibrium. Objects with different temperatures are not in thermal equilibrium."
These are ideas everyone has a vague understanding of. However, to state them in this way required that we ask a question about what defines the relationship between temperature and thermal equilibrium, which is not what most people would jump to when considering the question "what is temperature?". Because there are other natural places to jump to when discussing temperature, we will discuss one below.
Temperature = Energy?
Short answer: No.
Many would be tempted to say that high temperature = lots of energy, and low temperature = not much energy. This would mean energy flows from objects which have lots of energy to objects which have less energy. This makes some sense. When you heat something up, energy is added to it. But there are some glaring problems with this view that should make you doubtful about the idea that temperature is a measure of energy.
Imagine a vast pool of water at room temperature. Clearly the water is not particularly hot, but due to its enormous size it contains lots of energy. Now imagine that a red-hot bead of metal is dropped into the pool of water. The tiny bead can't possibly have more energy in it than the large pool of water. And yet what happens? When the bead plops into the water, heat flows from the bead to the water. This is where we run into the problem that energy is extensive, which means it scales with the amount of matter present, while temperature is intensive, meaning its value does not depend on the size of the system. Thus the huge pool has lots of energy, but has a lower temperature than the bead.
One might then go ahead and guess that maybe temperature is energy divided by volume, so that as the object gets bigger, the change in size is compensated for and the temperature doesn't change. This seems very encouraging! An Olympic swimming pool and a glass of water would now have the same temperature, because the energy density is the same across the two objects. We now have a metric which is intensive rather then extensive, just like temperature.
But this is not temperature: this idea runs into problems when one considers multiple substances interacting. Consider a pot of water and a block of iron, having equal volumes, which we have held in contact with each other long enough that their temperatures are now the same. Imagine that we separate them and add the same amount of energy to each, say by heating it by a fire. If temperature is energy per volume, then when brought back together the two should have the same temperature, since they have the same energy and the same volume. However, when performed in real life, the iron comes out hotter than the water.
Clearly there is some connection between temperature and energy, but it is not so simple as either of these (intuitive) guesses make it seem. This is why you are encouraged to think of temperature as a measure of "hotness" for now — of whether it will be in thermal equilibrium with other systems — until you know more about energy and the concept of entropy. If that sounds vague and unsatisfying, you are in good company, as many of the scientists who helped developed thermodynamics were motivated to uncover what is meant by temperature.
Quick Note on Units
The SI unit of temperature is Kelvin, which is what you should assume is being used here at all times. Temperatures are commonly measured in degrees Celsius and Fahrenheit, so it's important to be able to convert from these to Kelvin.
For a Celsius-Kelvin conversion, matters are simple because a one degree difference in Celsius is also a one Kelvin difference. The difference is only the zero-point: zero Kelvin is -273.15 degrees Celsius. Similarly, zero degrees Celsius is 273.15 Kelvin.
If you do encounter a temperature in degrees Fahrenheit, I would personally just use Google to convert to Kelvin. Regardless, it can be useful to remember that the freezing point of water is 0 degrees Celsius, and 32 degrees Fahrenheit. If you also remember that water boils at 100 degrees Celsius and 212 degrees Fahrenheit, you should be able to convert any other temperature with knowledge about linear equations.
Note: Unsurprisingly, Kelvin, degrees Celsius, and degrees Fahrenheit are abbreviated as K, °C, and °F, respectively. Note that Kelvin does not come with a degree symbol or prefix.
Exercise With Units
If, in a particular situation, we care about the ratio of one temperature to another (e.g. \( \frac{T_{1}}{T_{2}} \) ), does it matter whether the temperatures are recorded in K, °C, or °F? (To be precise, does the choice of units for T1 and T2 affect the outcome of the computation?) Compare an easy pair of temperatures as an example to help you decide on an answer.
In a different situation, it is the difference of two temperatures that matter (e.g. T1 - T2). Argue that we can use two temperatures in K or two temperatures in °C, and get the same answer either way.
Heat
People tend to use words like heat, temperature, and thermal energy interchangeably. However, in physics, these words can never be used in place of each other. They each mean something different. We already saw how temperature refers to something which is related to energy, but is definitely not energy. What is meant by heat then?
Heat in Physics, Definition
In physics, heat is energy that spontaneously passes between a system and its surroundings in some way other than through work or the transfer of matter. When a suitable physical pathway exists, heat flows spontaneously from a hotter to a colder body.
Heat is (unfortunately) usually denoted in equations with an upper-case Q. The upper-case H is used elsewhere in thermodynamics, for what we call "enthalpy".
Ignoring the statement about "work" for a moment, this definition says that heat is energy, but of a very specific type:
Heat is energy that is flowing spontaneously from hot to cold.
Notice how the word used is flow-ing, with an 'ing' at the end. This is because heat refers only to energy which is being transferred actively from one object to another. A hot object does not 'have' heat. The word you should use there is high temperature. A correct statement would be "heat flows from the metal to the water in the beaker."
Exercise: Using Words Correctly
Which of the following statements uses physics terms correctly?
(1) "The metal block is hot because it has more thermal energy than the beaker of water."
(2) "Two objects in thermal equilibrium have equal heat."
(3) "Heat ceases to flow when objects reach thermal equilibrium."
(4) "An object with higher temperature is touched to an object of lower temperature. Heat flows from the hot object to the cold object."
(5) "Heat is a measure of an object's thermal energy."
(6) "When you touch a hot object, you feel the heat."
Answer are at the bottom of the page.
Getting Quantitative
In the 1740's, scientists noticed that there was a relationship between energy and temperature. (Previously, scientists believed that there was an invisible fluid called "caloric" which was responsible for an objects temperature, and which would flow from hot objects to cold objects). Of course it's easy to look back and exclaim that those ideas were silly, but keep in mind that energy was not understood to be a fundamental part of physics in that time, and that the concept of energy conservation was not well developed. As such, the straightforward conclusion we draw today — that when energy as heat enters an object, it's internal energy increases by exactly that amount — would not have made a huge amount of sense then. It was not until Joule performed the work-heat equivalence experiment that the scientific community accepted heat and thermal energy as being "real" energy forms.
Subsequently, huge numbers of experiments were conducted to iron out the relationship between temperature and thermal energy. The result of this investigation is best summarized with the following statement:
For small changes in T and U,
\[ \Delta U \propto \Delta T \]
The symbol there means "proportional to", which means there is a typically linear relationship between thermal energy added to an object and the amount that the object's temperature changes (when the object is not undergoing a phase-change). To bridge the proportionality gap, we introduce a constant, c, which depends heavily on the material in question, as well as its phase, and to some extent its temperature.
Temperature and Thermal Energy: Specific Heat
\[ \Delta U = mc \Delta T \]
or
\[ c = \frac{1}{m} \frac{ \Delta U}{ \Delta T} \]
This equation describes the empirically determined relationship between the change in an objects internal energy, \( \Delta U \), and the corresponding change in the object's temperature, \( \Delta T \).
The object's mass, m, is included in this form of the equation so that one constant, c, can be used for any amount of substance present. The constant, c, is what we call the "specific heat" of the substance, and is empirically determined. The second form of the equation is essentially a definition of specific heat.
NOTE: The name "specific heat" is, all physicists agree, an absolutely terrible name. It is a misnomer, and a remnant of the time when there was believed to be a difference between heat and energy. It should be "specific energy", as energy can enter the object in any form, not just as heat.
To get a feel for the ranges of specific heat, take a look at this table of specific heats for various substances (look at the first column.) Key values of c to look at: for water, c is 4186 joules per kilogram kelvin. For solid lead, c is 127 J/kg K.
Example: Heating Water
 A pot of water (say, 1 liter), is brought from room temperature (23 °C) to a boil (100 °C). How much energy must have flowed into the water during this process? (The specific heat of water is 4186 J/kg K.)
A pot of water (say, 1 liter), is brought from room temperature (23 °C) to a boil (100 °C). How much energy must have flowed into the water during this process? (The specific heat of water is 4186 J/kg K.)
Solution:
Thanks to others who have determined the specific heat of water by doing this very experiment, we can solve for the energy change easily.
\[ mc \Delta T = \Delta U \]
Since the density of water is 1 kg/L, m = 1 kg. Also note that since kelvin and degrees Celsius are the same during subtraction, no conversion is necessary. In other cases, where temperatures are divided for example, you will need to convert before computing.
\[ (1 kg)(4,186 J/kg K)(100.0 - 23.0 K) = 322,322 J \]
Extra: How Does This Energy Compare?
The kinetic energy, K, of an object is calculated as follows: \( K = \frac{1}{2} mv^{2} \)
Where m is the object's mass in kilograms, and v is the object's speed, in meters per second. How does the kinetic energy of a small car (m = 2000 kg) on the freeway (speed is 80 km/hr) compare to the energy required to boil a pot of water?
First, convert km/hr to m/s:
\[ \left( \frac{80 \text{ kilometers}}{1 \text{ hour}} \right) \left( \frac{ 1 \text{ hour}}{3,600 \text{ seconds}} \right) \left( \frac{1,000 \text{ meters}}{1 \text{ kilometer}} \right) = 22.2 m/s\]
Next, calculate the kinetic energy:
\[ K = \frac{1}{2}(2,000 kg)(22.2 m/s)^{2} = 493,827 J \]
This is larger than the energy required to boil the water — but not much larger. If the pot of water were 2 liters rather than 1 liter, then the car would be losing! It turns out that bringing water to a boil uses about as much energy as accelerating a car up to highway speeds.
You will learn next about what happens when the water is actually boiling, a point which we've swept under the rug until this point. (Spoiler: boiling water takes a lot more energy than bringing it to a boil.)
Example: Coming to Equilibrium
A 50g block of aluminum is dropped into a beaker with 300g of water. The initial temperature of the block is 200 °C, and the water is at room temperature (23 °C). What is the final temperature after equilibrium is reached? (The specific heat of water and aluminum are 4186 J/kg K and 900 J/kg K, respectively.)
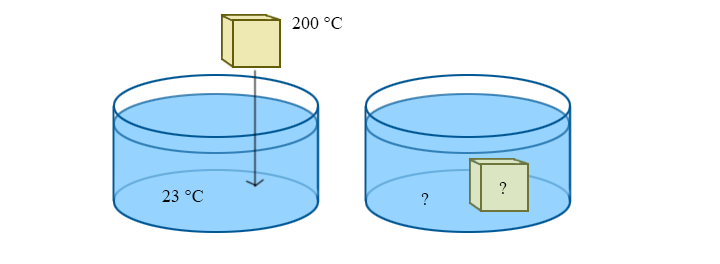
Solution
Assuming that negligible heat is leaked to the environment, we can use the specific heat equation to solve for the final temperature, Tf. At equilibrium, we know that the final temperature of the block and the water are the same: Tf, block = Tf, water = Tf
We also know from energy conservation that the amount of energy as heat that flows out of the block is the same as the amount of energy that flows into the water. We can express this by saying that \( \Delta U_{water} = - \Delta U_{block} \).
We're left with a system of equations:
\[ \Delta U_{b} = m_{b}c_{b} \Delta T_{b} \]
\[ \Delta U_{w} = m_{w}c_{w} \Delta T_{w} \]
We can write the change in temperature as \( \Delta T_{b} = T_{f} - T_{i,b} \) and \( \Delta T_{w} = T_{f} - T_{i,w} \). Using the the fact that \( \Delta U_{water} = - \Delta U_{block} \), we have
\[ \Delta U = m_{b}c_{b} (T_{f} - T_{i,w}) \]
\[ - \Delta U = m_{w}c_{w} (T_{f} - T_{i,b}) \]
From here, it is a simply a matter of solving the system of equations for Tf. After doing this, you should get:
\[ T_{f} = \frac{ m_{w}c_{w}T_{i,w} + m_{b}c_{b}T_{i,b} }{ m_{w}c_{w} + m_{b}c_{b} } \]
Notice how the form of this equation is a weighted average of temperature. The answer will always be between Ti,b and Ti,w, but will be closer to the initial temperature of the object with a larger mass-specific-heat product. This makes sense: it's essentially saying that it takes more energy to change the temperature of a bigger object. Using the given numbers, this tells us that the final temperature is 29.1 °C. Notice how much closer to the starting temperature of the water this is than the starting temperature of the aluminum.
Answers to Exercises
(1) "The metal block is hot because it has more thermal energy than the beaker of water."
Incorrect. As discussed, an object's temperature is intensive, while its energy is extensive. It is possible that the water has more energy, but the block is still hotter.
(2) "Two objects in thermal equilibrium have equal heat."
Incorrect usage of heat. Heat is a transfer of energy. An object does not 'have' heat.
(3) "Heat ceases to flow when objects reach thermal equilibrium."
Correct. Two objects in thermal equilibrium are the same temperature. Heat only flows when there is a difference in temperature.
(4) "An object with higher temperature is touched to an object of lower temperature. Heat flows from the hot object to the cold object."
Correct. This is essentially the definition of heat.
(5) "Heat is a measure of an object's thermal energy."
Incorrect. Heat is energy which moves, and can take any value independently of the thermal energy.
(6) "When you touch a hot object, you feel the heat."
Technically correct. What your nerves tell you that an object is "hot", it is the heat which flows from the object to your skin that you are feeling.


