1.3: Three Phase Model of Matter
( \newcommand{\kernel}{\mathrm{null}\,}\)
The goal of this section is simply to extend the naive discussion of energy and temperature we have running so far to include phase changes. I use the word naive in the sense that, at this point in the course, we still don't understand what the underlying mechanisms in thermal phenomena really are. There were a lot of questions and only a few half-answers on the previous page. Keep in mind that the take away from these first sections are not fundamental, but are still of value. Firstly, they can be applied to predict a fairly wide range of phenomena involving heat and energy transfers. Secondly, and more importantly, they create a framework for the more fundamental ideas to attach to. For example, when a theory comes along claiming to be about the underlying mechanisms of temperature, it can attach to and be tested against this basic framework. Does the theory explain the connection between thermal equilibrium and temperature? Does the theory explain the phases of matter? How does this theory predict the widely varied values of specific heat and "latent heat" (which we are about to learn about).
Pure Substances Have a Phase
We adopt the standard chemistry definition that a substance is any material with a definite chemical composition. By “pure,” we simply mean that only one chemical substance is present in the sample. So, water has a definite phase, but mixtures (like oobleck) do not. This is partly a disclaimer so that questions such as "is glass a liquid or a solid?" can be put out of mind for now. For the first pass at this model, we treat pure substances as though they are in one of three phases: solid, liquid, or gas.
Note that we are choosing which relevant features to include in our model and which to exclude. The choices will definitely affect the level of detail we can address in our questions and discuss in our explanations. At this time, we are deliberately choosing to be more general to keep the model as simple as possible and at the same time, applicable to as wide a range of phenomena as possible.
Phases Can Be Determined by Temperature and Pressure
Pictured below is the "phase diagram" for water in temperature-pressure space.
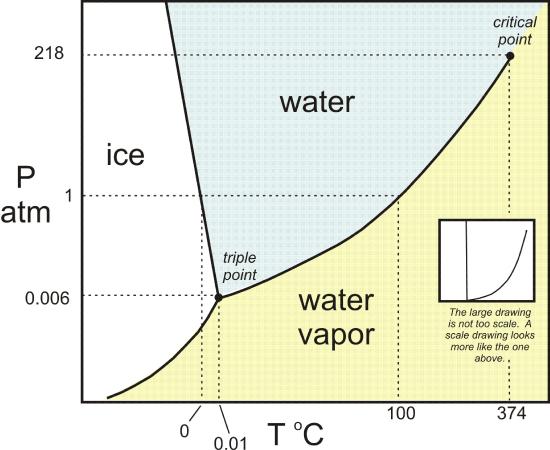
With temperature on the x-axis, and pressure on the y-axis, the diagram indicates which situations water is observed to be solid (ice), liquid (water), or gas (water vapor).
If you follow the horizontal dotted line at 1 atm, you should recover the common freezing and boiling points: 0 °C and 100 °C.
The following ideas are not important enough to try to remember them, but they're interesting.
The phase diagrams of pure substances all share this basic shape, but vary greatly in where exactly the phases occur in temperature-pressure space. Single phase regions are separated by lines, where phase transitions occur, which are called phase boundaries.
The phase boundary between liquid and gas does not continue indefinitely. Instead, it terminates at a point on the phase diagram called the critical point. This reflects the fact that, at extremely high temperatures and pressures, the liquid and gaseous phases become indistinguishable, in what is known as a supercritical fluid. In water, the critical point occurs at around Tc = 647.1 K (374.0 °C) and pc = 22.064 MPa (217.75 atm). In conditions more extreme than this, the liquid and gas phases become indistinguishable from one another in the sense that there is no longer a boiling point, but rather a smooth transition from gas to liquid.
When conditions are on a phase boundary, multiple phases can coexist within the substance. For example, at boiling point, water will transition spontaneously back and forth between liquid and gas. The special boundary point where all three phases can coexist is called the triple point. Check out what the triple point of water looks like here.
Energy and Phase Changes
In much the same way scientists observed a linear connection between energy input and temperature for pure substances in a single phase, there is a simple relationship between energy input and phase change. The trend is best summarized with a diagram.
Temperature vs. Energy Added
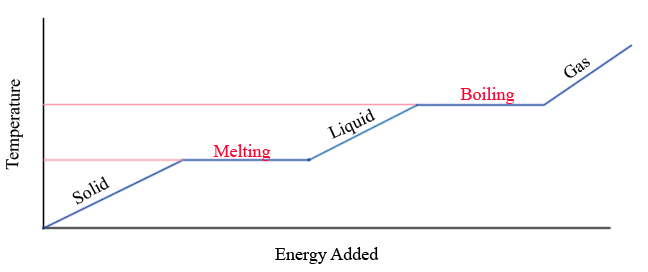
The important thing to notice is that during a phase change, temperature remains constant even while energy is being added. In real life, this could be tested by boiling a pot of water while measuring temperature with a thermometer. If you do this yourself, you will find that the water temperature remains at exactly 100 °C throughout the boiling process. Even as the flame continues to pour heat into the pot-water system, the water's temperature will not change until all the water is boiled away.
In the simplest form of the Three-Phase Model of Matter, the phase changes occur at the same temperature “on the way down” as “on the way up.” That is, the temperature of the change from liquid to solid as energy is removed is the same as the temperature of the phase change from solid to liquid as energy is added. Due to this symmetry, the liquid-solid or solid-liquid phase change temperature can be referred to as either the freezing or melting temperature. Likewise at the boiling point, the phase change temperature can be referred to as the boiling or condensation temperature.
Summary of Possible Phase Transitions
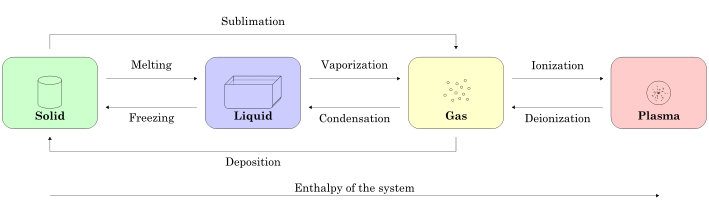
(Don't worry about plasma or enthalpy for now.)
The question often arises: "why does water at room temperature evaporate?". Everyone knows that leaving something out to dry does not require heating said object to 212 °F, and yet that seems to be what we've been saying thus far. The answer relies on substances being made of an enormous number of particles, and temperature being a measure of an average over that large number of particles. It is possible that individual particles can be spontaneously given enough energy to escape the liquid and fly off into the air, at which point that particle has "boiled". In fact, you can calculate an expected rate for this to occur (which we won't do right now).
Latent Heat
Suppose you have noticed that water does not change temperature while boiling. Once you have a way to measure the amount of energy being added to the water. it is then a sensible next step to ask: "How much energy does it take to boil the water?". Performing this exact experiment will leave you with the specific latent heat of water. The word latent comes from Latin, meaning lying hidden. The reasoning behind this title is that energy added or removed during phase changes seems to be "hidden", in that it does not show up as a change in temperature.
Energy of a Phase Change
The specific latent heat, L, expresses the amount of energy E required to convert a pure substance of mass m entirely from one phase to another with no change in temperature.
L=Em
The equation is more commonly written solved for the energy, since we often know the specific latent heat, and wish to know the energy of phase change.
E=mL
The energy is often (confusingly) called the latent heat, without the "specific" in front. In this case, it is often written using the heat Q rather than the more general energy E. This acknowledges that phase change energy commonly enters a system as heat. However, the more general "energy" encompass the fact that the energy can really enter in any form, so long as it eventually becomes internal energy of the substance changing phases.
The value of various specific latent heats are readily available online.
Example: Melting Gold and Water
How much energy does it take to melt 1 kg of ice? How much energy does it take to melt 1 kg of gold?
Solution
This problem just comes down to looking the answers up online. Quoted from a quick Google search:
"The specific latent heat of fusion of ice is the amount of heat required to change 1 kg of ice to water without a change in temperature. The specific latent heat of fusion of ice is 0.336 MJ/kg "
Similarly, a quick search should reveal that the specific latent heat of fusion of gold is around 65.0 kJ/kg.
Surprisingly, the energy required to melt ice is much greater than the amount of energy required to melt gold! You may have already encountered this fact from chemistry, but if you have not, try to think about why this might be the case.
Example: Putting Phase and Temperature Together
Imagine 0.30 kg of ice at 0 °C is added to 1.0 kg of water at 45 °C. What is the final temperature after the water comes to equilibrium, assuming no heat exchange with the surroundings? Take the specific heat capacity of water to be 4200 J/kg K and the specific latent heat of fusion of ice to be 3.4 × 105 J/kg.
Solution
Let Tf be the final temperature.
By energy conservation, the heat lost by the water must be equal to the heat gained in melting the ice, plus the heat gained in warming the ice water.\( m_{w}c_{w} \Delta
Tw=miceLice+micecwΔTmelted ice
mwcw(Tf–45)=miceLice+micecw(Tf−0)
Replacing the numbers back in and solving for Tf,
(1kg)(4200J/kg K)(45°C–Tf)=(0.30kg)(3.4×105J/kg)+(0.3kg)(4200J/kg K)Tf
(4200J/kg K)(45°C–Tf)=1.02×105J+(1260J/K)Tf
1.89×105J–1.02×105J=(1260J/K)Tf+(4200J/K)Tf
Tf=16°C
Why Sweating?
Explain why sweating is an effective means of cooling ourselves down.


