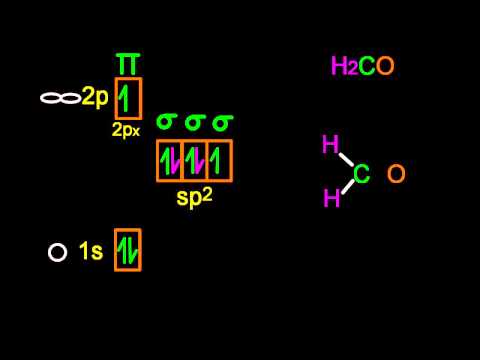
19.14: Hybrid Orbitals - sp and sp²
- Page ID
- 102033
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Figure \(\PageIndex{1}\) (Public Domain; Frank Dicksee via Wikipedia)
How do you open the closed circle?
Romeo and Juliet were two of the greatest-known fictional lovers of all time. Their embrace allowed no other person to be a part of it—they only wanted to be with each other. It took outside intervention to get them away from one another. Paired electrons are similar to Romeo and Juliet. They do not bond covalently until they are unpaired; then, they can become a part of a larger chemical structure.
sp Hybridization
A beryllium hydride \(\left( \ce{BeH_2} \right)\) molecule is predicted to be linear by VSEPR. The beryllium atom contains all paired electrons and so must also undergo hybridization. One of the \(2s\) electrons is first promoted to the empty \(2p_x\) orbital (see figure below).
Figure \(\PageIndex{2}\): Promotion of \(\ce{Be}\) \(2s\) electron. (CC BY-NC 3.0; Joy Sheng via CK-12 Foundation)
Now the hybridization takes place only with occupied orbitals, and the result is a pair of \(sp\) hybrid orbitals. The two remaining \(p\) orbitals (\(p_y\) and \(p_z\)) do not hybridize and remain unoccupied (see figure below).
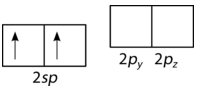Figure \(\PageIndex{3}\): \(\ce{Be}\) hybrid orbitals. (CC BY-NC 3.0; Joy Sheng via CK-12 Foundation)
The geometry of the \(sp\) hybrid orbitals is linear, with the lobes of the orbitals pointing in opposite directions along one axis, arbitrarily defined as the \(x\)-axis (see figure below). Each can bond with a \(1s\) orbital from a hydrogen atom to form the linear \(\ce{BeH_2}\) molecule.
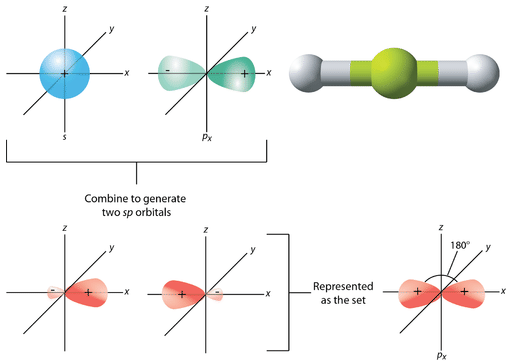Figure \(\PageIndex{4}\): The process of \(sp\) hybridization is the mixing of an \(s\) orbital with a single \(p\) orbital (the \(p_x\) orbital by convention), to form a set of two \(sp\) hybrids. The two lobes of the \(sp\) hybrids point opposite one another to produce a linear molecule. (CC BY-NC 3.0 (3D molecule available under public domain; Jodi So, using 3D molecule by Ben Mills (User: Benjah-bmm27/Wikimedia Commons via CK-12 Foundation; 3D molecule: http://commons.wikimedia.org/wiki/File:Beryllium-hydride-molecule-IR-3D-balls.png))
Other molecules whose electron domain geometry is linear and for whom hybridization is necessary also form \(sp\) hybrid orbitals. Examples include \(\ce{CO_2}\) and \(\ce{C_2H_2}\), which will be discussed in further detail later.
sp² Hybridization
Boron trifluoride \(\left( \ce{BF_3} \right)\) is predicted to have a trigonal planar geometry by VSEPR. First, a paired \(2s\) electron is promoted to the empty \(2p_y\) orbital (see figure below).
Figure \(\PageIndex{5}\): Promotion of \(2s\) electron. (CC BY-NC 3.0; Joy Sheng via CK-12 Foundation)
This is followed by hybridization of the three occupied orbitals to form a set of three \(sp^2\) hybrids, leaving the \(2p_z\) orbital unhybridized (see figure below).
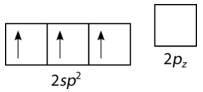Figure \(\PageIndex{6}\): Formation of \(sp^2\) orbital. (CC BY-NC 3.0; Joy Sheng via CK-12 Foundation)
The geometry of the \(sp^2\) hybrid orbitals is trigonal planar, with the lobes of the orbitals pointing towards the corners of a triangle (see figure below). The angle between any two of the hybrid orbital lobes is \(120^\text{o}\). Each can bond with a \(2p\) orbital from a fluorine atom to form the trigonal planar \(\ce{BF_3}\) molecule.
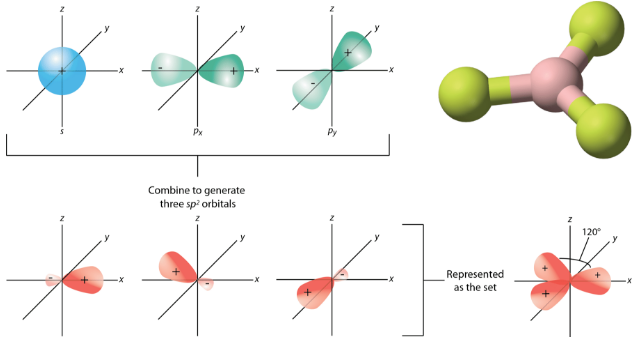Figure \(\PageIndex{7}\): The process of \(sp^2\) hybridization is the mixing of an \(s\) orbital with a set of two \(p\) orbitals (\(p_x\) and \(p_y\)) to form a set of three \(sp^2\) hybrid orbitals. Each large lobe of the hybrid orbital points to one corner of a planar triangle. (CC-BY-NC 3.0 (3D molecule available under the public domain; CK-12 Foundation - Jodi So, using 3D molecular structure by Ben Mills (Wikimedia: Benjah-bmm27) via 3D molecule: http://commons.wikimedia.org/wiki/File:Boron-trifluoride-3D-balls.png))
Other molecules with a trigonal planar electron domain geometry form \(sp^2\) hybrid orbitals. Ozone \(\left( \ce{O_3} \right)\) is an example of a molecule whose electron domain geometry is trigonal planar, though the presence of a lone pair on the central oxygen makes the molecular geometry bent. The hybridization of the central \(\ce{O}\) atom of ozone is \(sp^2\).
Summary
- Paired electrons can be hybridized and then participate in covalent bonding.
Review
- Does the ground state beryllium atom contain any unpaired electrons?
- Why does one 2s electron in Be get promoted to a 2p orbital?
- What is the geometry of the two sp orbitals?