2.6: Two Semicylindrical Electrodes

This section requires that the reader should be familiar with functions of a complex variable and conformal transformations. For readers not familiar with these, this section can be skipped without prejudice to understanding following chapters. For readers who are familiar, this is a nice example of conformal transformations to solve a physical problem.

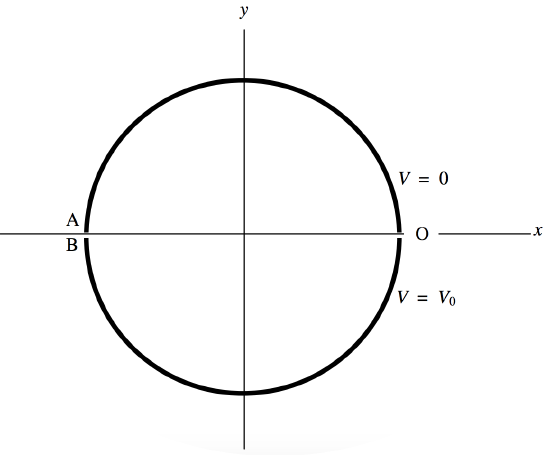
$\text{FIGURE II.5}$

We have two semicylindrical electrodes as shown in Figure $II$.5. The potential of the upper one is 0 and the potential of the lower one is $V_0$. We'll suppose the radius of the circle is 1; or, what amounts to the same thing, we'll express coordinates $x$ and $y$ in units of the radius. Let us represent the position of any point whose coordinates are (x , y) by a complex number $z = x + iy$.

Now let $w = u + iv$ be a complex number related to $z$ by $w=i\left (\frac{1-z}{1+z}\right )$; that is, $z=\frac{1+ iw}{1- iw}$. Substitute $w = u + iv \text{ and }z = x + iy$ in each of these equations, and equate real and imaginary parts, to obtain

$$\begin{align}\label{2.6.1}u&=\frac{2y}{(1+x)^2+y^2};\quad\quad &&v=\frac{1-x^2+y^2}{(1+x)^2+y^2};\\ x&=\frac{1-u^2-v^2}{u^2+(1+v)^2}; &&y=\frac{2u}{u^2+(1+v)^2}.\label{2.6.2}\end{align}$$

In that case, the upper semicircle $(V = 0)$ in the $xy$-plane maps on to the positive $u$-axis in the $uv$-plane, and the lower semicircle $(V = V_0)$ in the $xy$-plane maps on to the negative $u$-axis in the $uv$-plane. (Figure $II$.6.) Points inside the circle bounded by the electrodes in the $xy$-plane map on to points above the $u$-axis in the $uv$-plane.

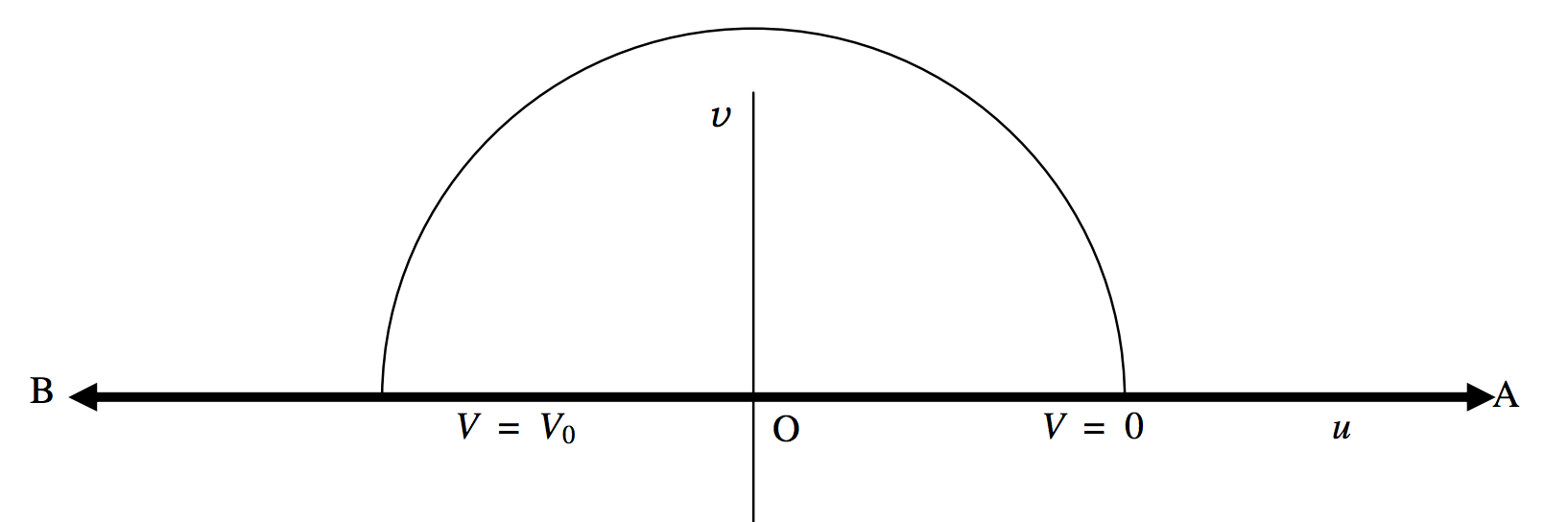
$\text{FIGURE II.6}$

In the $uv$-plane, the lines of force are semicircles, such as the one shown. The potential goes from 0 at one end of the semicircle to $V_0$ at the other, and so equation to the semicircular line of force is

$$\label{2.6.3}\frac{V}{V_0}=\frac{\text{arg}\,w}{\pi}$$

or

$$\label{2.6.4}V=\frac{V_0}{\pi}\tan^{-1}(v/u).$$

The equipotentials ($V$ = constant) are straight lines in the $uv$-plane of the form

$$\label{2.6.5}v=fu.$$

(You would prefer me to use the symbol $m$ for the slope of the equipotentials, but in a moment you will be glad that I chose the symbol $f$.)

If we now transform back to the $xy$-plane, we see that the equation to the lines of force is

$$\label{2.6.6}V=\frac{V_0}{\pi}\tan^{-1} \left (\frac{1-x^2-y^2}{2y}\right ).$$

and the equation to the equipotentials is

$$\label{2.6.7}1-x^2-y^2=2fy,$$

or

$$\label{2.6.8}x^2+y^2+2fy-1=0$$

Now aren't you glad that I chose $f$ ? Those who are handy with conic sections (see Chapter 2 of Celestial Mechanics) will understand that the equipotentials in the $xy$-plane are circles of radii $\sqrt{f^2 + 1}$, whose centres are at $(0 , \pm f )$, and which all pass through the points $(\pm 1 , 0)$. They are drawn as blue lines in Figure $II$.7. The lines of force are the orthogonal trajectories to these, and are of the form

$$\label{2.6.9}x^2+y^2+2gy+1=0$$

These are circles of radii $\sqrt{g^2 −1}$ and have their centres at $(0 , \pm g)$. They are shown as dashed red lines in Figure $II$.7.

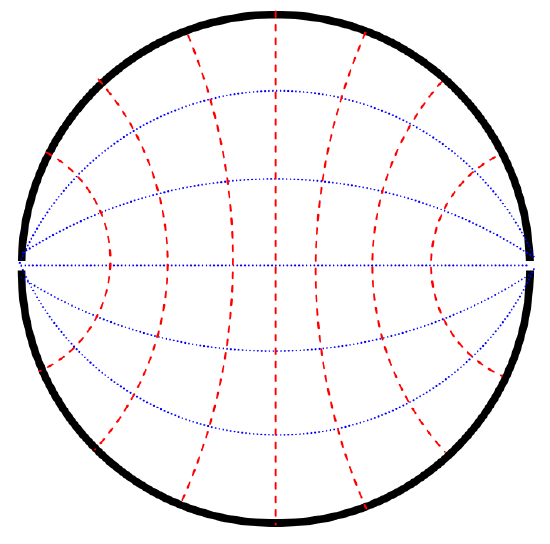
$\text{FIGURE II.7}$