5.19: Charging a Capacitor Through a Resistor
( \newcommand{\kernel}{\mathrm{null}\,}\)
This time, the charge on the capacitor is increasing, so the current, as drawn, is +˙Q.
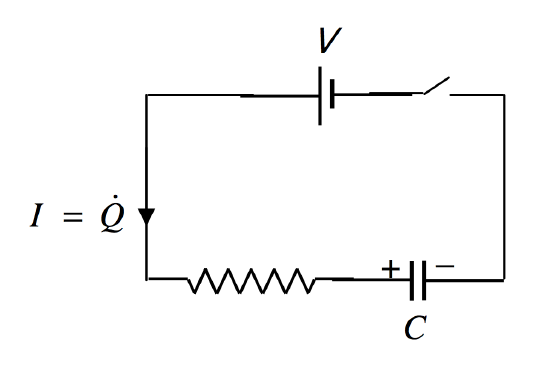
FIGURE V.25
Thus
V−˙QR−QC=0
Whence:
∫Q0dQCV−Q=1RC∫t0dt.
Remember that, at any finite t, Q is less than its asymptotic value CV, and you want to keep the denominator of the left hand integral positive.
Upon integrating Equation ???, we obtain
Q=CV(1−e−t/(RC)).
Thus the charge on the capacitor asymptotically approaches its final value CV, reaching 63% (1 - e-1) of the final value in time RC and half of the final value in time RCln2=0.6931RC.
The potential difference across the plates increases at the same rate. Potential difference cannot change instantaneously in any circuit containing capacitance.
How does the current change with time? This is found by differentiating Equation ??? with respect to time, to give
I=VRe−t/(RC).
This suggests that the current grows instantaneously from zero to V/R as soon as the switch is closed, and then it decays exponentially, with time constant RC, to zero. Is this really possible? It is possible in principle if the inductance (see Chapter 12) of the circuit is zero. But the inductance of any closed circuit cannot be exactly zero, and the circuit, as drawn without any inductance whatever, is not achievable in any real circuit, and so, in a real circuit, there will not be an instantaneous change of current. Section 10.15 will deal with the growth of current in a circuit that contains both capacitance and inductance as well as resistance.
Energy considerations
When the capacitor is fully charged, the current has dropped to zero, the potential difference across its plates is V (the EMF of the battery), and the energy stored in the capacitor (see Section 5.10) is
12CV2=12QV.
But the energy lost by the battery is QV. Let us hope that the remaining 12QV is heat generated in and dissipated by the resistor. The rate at which heat is generated by current in a resistor (see Chapter 4 Section 4.6) is I2R. In this case, according to the previous paragraph, the current at time t is
I=VRe−t/(RC),
so the total heat generated in the resistor is
V2R∫∞0e−2t/(RC)=12CV2,
so all is well. The energy lost by the battery is shared equally between R and C.
Neon lamp
Here’s a way of making a neon lamp flash periodically.
In Figure V.2512 (sorry about the fraction – I slipped the Figure in as an afterthought!), the thing that looks something like a happy face on the right is a discharge tube; the dot inside it indicates that it’s not a complete vacuum inside, but it has a little bit of gas inside.
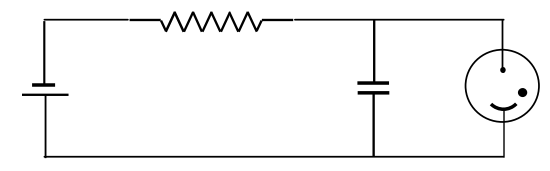
FIGURE V.2512
It will discharge when the potential difference across the electrodes is higher than a certain threshold. When an electric field is applied across the tube, electrons and positive ions accelerate, but are soon slowed by collisions. But, if the field is sufficiently high, the electrons and ions will have enough energy on collision to ionize the atoms they collide with, so a cascading discharge will occur. The potential difference rises exponentially on an RC time-scale until it reaches the threshold value, and the neon tube suddenly discharges. Then it starts all over again.
There is a similar problem involving an inductor in Chapter 10, Section 10.12.


