24.1: Introducing General Relativity
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Discuss some of the key ideas of the theory of general relativity
- Recognize that one’s experiences of gravity and acceleration are interchangeable and indistinguishable
- Distinguish between Newtonian ideas of gravity and Einsteinian ideas of gravity
- Recognize why the theory of general relativity is necessary for understanding the nature of black holes
Most stars end their lives as white dwarfs or neutron stars. When a very massive star collapses at the end of its life, however, not even the mutual repulsion between densely packed neutrons can support the core against its own weight. If the remaining mass of the star’s core is more than about three times that of the Sun (MSun), our theories predict that no known force can stop it from collapsing forever! Gravity simply overwhelms all other forces and crushes the core until it occupies an infinitely small volume. A star in which this occurs may become one of the strangest objects ever predicted by theory—a black hole.
To understand what a black hole is like and how it influences its surroundings, we need a theory that can describe the action of gravity under such extreme circumstances. To date, our best theory of gravity is the general theory of relativity, which was put forward in 1916 by Albert Einstein.
General relativity was one of the major intellectual achievements of the twentieth century; if it were music, we would compare it to the great symphonies of Beethoven or Mahler. Until recently, however, scientists had little need for a better theory of gravity; Isaac Newton’s ideas that led to his law of universal gravitation (see Orbits and Gravity) are perfectly sufficient for most of the objects we deal with in everyday life. In the past half century, however, general relativity has become more than just a beautiful idea; it is now essential in understanding pulsars, quasars (which will be discussed in Active Galaxies, Quasars, and Supermassive Black Holes), and many other astronomical objects and events, including the black holes we will discuss here.
We should perhaps mention that this is the point in an astronomy course when many students start to feel a little nervous (and perhaps wish they had taken botany or some other earthbound course to satisfy the science requirement). This is because in popular culture, Einstein has become a symbol for mathematical brilliance that is simply beyond the reach of most people (Figure 24.1.1).

So, when we wrote that the theory of general relativity was Einstein’s work, you may have worried just a bit, convinced that anything Einstein did must be beyond your understanding. This popular view is unfortunate and mistaken. Although the detailed calculations of general relativity do involve a good deal of higher mathematics, the basic ideas are not difficult to understand (and are, in fact, almost poetic in the way they give us a new perspective on the world). Moreover, general relativity goes beyond Newton’s famous “inverse-square” law of gravity; it helps explain how matter interacts with other matter in space and time. This explanatory power is one of the requirements that any successful scientific theory must meet.
The Principle of Equivalence
The fundamental insight that led to the formulation of the general theory of relativity starts with a very simple thought: if you were able to jump off a high building and fall freely, you would not feel your own weight. In this chapter, we will describe how Einstein built on this idea to reach sweeping conclusions about the very fabric of space and time itself. He called it the “happiest thought of my life.”
Einstein himself pointed out an everyday example that illustrates this effect (Figure 24.1.2). Notice how your weight seems to be reduced in a high-speed elevator when it accelerates from a stop to a rapid descent. Similarly, your weight seems to increase in an elevator that starts to move quickly upward. This effect is not just a feeling you have: if you stood on a scale in such an elevator, you could measure your weight changing (you can actually perform this experiment in some science museums).
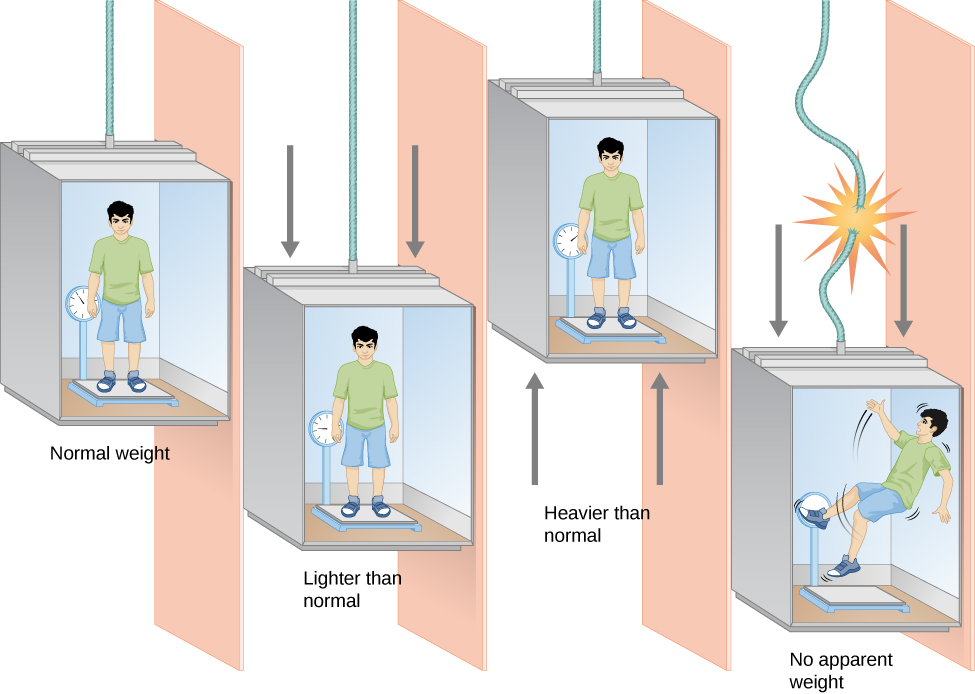
In a freely falling elevator, with no air friction, you would lose your weight altogether. We generally don’t like to cut the cables holding elevators to try this experiment, but near-weightlessness can be achieved by taking an airplane to high altitude and then dropping rapidly for a while. This is how NASA trains its astronauts for the experience of free fall in space; the scenes of weightlessness in the 1995 movie Apollo 13 were filmed in the same way. (Moviemakers have since devised other methods using underwater filming, wire stunts, and computer graphics to create the appearance of weightlessness seen in such movies as Gravity and The Martian.)
Watch how NASA uses a “weightless” environment to help train astronauts.
Another way to state Einstein’s idea is this: suppose we have a spaceship that contains a windowless laboratory equipped with all the tools needed to perform scientific experiments. Now, imagine that an astronomer wakes up after a long night celebrating some scientific breakthrough and finds herself sealed into this laboratory. She has no idea how it happened but notices that she is weightless. This could be because she and the laboratory are far away from any source of gravity, and both are either at rest or moving at some steady speed through space (in which case she has plenty of time to wake up). But it could also be because she and the laboratory are falling freely toward a planet like Earth (in which case she might first want to check her distance from the surface before making coffee).
What Einstein postulated is that there is no experiment she can perform inside the sealed laboratory to determine whether she is floating in space or falling freely in a gravitational field.1 As far as she is concerned, the two situations are completely equivalent. This idea that free fall is indistinguishable from, and hence equivalent to, zero gravity is called the equivalence principle.
Gravity or Acceleration?
Einstein’s simple idea has big consequences. Let’s begin by considering what happens if two foolhardy people jump from opposite banks into a bottomless chasm (Figure 24.1.3). If we ignore air friction, then we can say that while they freely fall, they both accelerate downward at the same rate and feel no external force acting on them. They can throw a ball back and forth, always aiming it straight at each other, as if there were no gravity. The ball falls at the same rate that they do, so it always remains in a line between them.
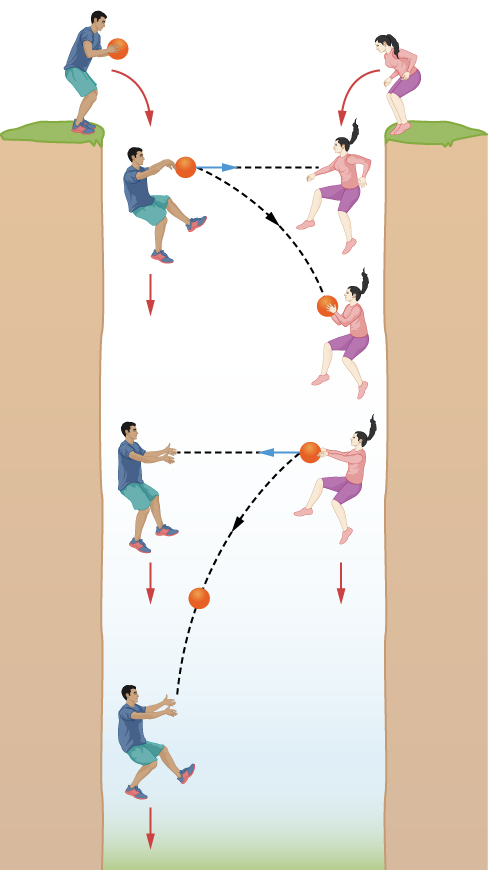
Such a game of catch is very different on the surface of Earth. Everyone who grows up feeling gravity knows that a ball, once thrown, falls to the ground. Thus, in order to play catch with someone, you must aim the ball upward so that it follows an arc—rising and then falling as it moves forward—until it is caught at the other end.
Now suppose we isolate our falling people and ball inside a large box that is falling with them. No one inside the box is aware of any gravitational force. If they let go of the ball, it doesn’t fall to the bottom of the box or anywhere else but merely stays there or moves in a straight line, depending on whether it is given any motion.
Astronauts in the International Space Station (ISS) that is orbiting Earth live in an environment just like that of the people sealed in a freely falling box (Figure 24.1.4). The orbiting ISS is actually “falling” freely around Earth. While in free fall, the astronauts live in a strange world where there seems to be no gravitational force. One can give a wrench a shove, and it moves at constant speed across the orbiting laboratory. A pencil set in midair remains there as if no force were acting on it.

In the “weightless” environment of the International Space Station, moving takes very little effort. Watch astronaut Karen Nyberg demonstrate how she can propel herself with the force of a single human hair.
Appearances are misleading, however. There is a force in this situation. Both the ISS and the astronauts continually fall around Earth, pulled by its gravity. But since all fall together—shuttle, astronauts, wrench, and pencil—inside the ISS all gravitational forces appear to be absent.
Thus, the orbiting ISS provides an excellent example of the principle of equivalence—how local effects of gravity can be completely compensated by the right acceleration. To the astronauts, falling around Earth creates the same effects as being far off in space, remote from all gravitational influences.
The Paths of Light and Matter
Einstein postulated that the equivalence principle is a fundamental fact of nature, and that there is no experiment inside any spacecraft by which an astronaut can ever distinguish between being weightless in remote space and being in free fall near a planet like Earth. This would apply to experiments done with beams of light as well. But the minute we use light in our experiments, we are led to some very disturbing conclusions—and it is these conclusions that lead us to general relativity and a new view of gravity.
It seems apparent to us, from everyday observations, that beams of light travel in straight lines. Imagine that a spaceship is moving through empty space far from any gravity. Send a laser beam from the back of the ship to the front, and it will travel in a nice straight line and land on the front wall exactly opposite the point from which it left the rear wall. If the equivalence principle really applies universally, then this same experiment performed in free fall around Earth should give us the same result.
Now imagine that the astronauts again shine a beam of light along the length of their ship. But, as shown in Figure 24.1.5, this time the orbiting space station falls a bit between the time the light leaves the back wall and the time it hits the front wall. (The amount of the fall is grossly exaggerated in Figure 24.1.5 to illustrate the effect.) Therefore, if the beam of light follows a straight line but the ship’s path curves downward, then the light should strike the front wall at a point higher than the point from which it left.
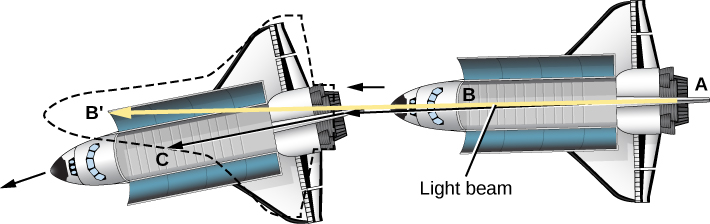
However, this would violate the principle of equivalence—the two experiments would give different results. We are thus faced with giving up one of our two assumptions. Either the principle of equivalence is not correct, or light does not always travel in straight lines. Instead of dropping what probably seemed at the time like a ridiculous idea, Einstein worked out what happens if light sometimes does not follow a straight path.
Let’s suppose the principle of equivalence is right. Then the light beam must arrive directly opposite the point from which it started in the ship. The light, like the ball thrown back and forth, must fall with the ship that is in orbit around Earth (see Figure 24.1.5). This would make its path curve downward, like the path of the ball, and thus the light would hit the front wall exactly opposite the spot from which it came.
Thinking this over, you might well conclude that it doesn’t seem like such a big problem: why can’t light fall the way balls do? But, as discussed in Radiation and Spectra, light is profoundly different from balls. Balls have mass, while light does not.
Here is where Einstein’s intuition and genius allowed him to make a profound leap. He gave physical meaning to the strange result of our thought experiment. Einstein suggested that the light curves down to meet the front of the shuttle because Earth’s gravity actually bends the fabric of space and time. This radical idea—which we will explain next—keeps the behavior of light the same in both empty space and free fall, but it changes some of our most basic and cherished ideas about space and time. The reason we take Einstein’s suggestion seriously is that, as we will see, experiments now clearly show his intuitive leap was correct.
Key Concepts and Summary
Einstein proposed the equivalence principle as the foundation of the theory of general relativity. According to this principle, there is no way that anyone or any experiment in a sealed environment can distinguish between free fall and the absence of gravity.
Footnotes
1Strictly speaking, this is true only if the laboratory is infinitesimally small. Different locations in a real laboratory that is falling freely due to gravity cannot all be at identical distances from the object(s) responsible for producing the gravitational force. In this case, objects in different locations will experience slightly different accelerations. But this point does not invalidate the principle of equivalence that Einstein derived from this line of thinking.
Glossary
- equivalence principle
- concept that a gravitational force and a suitable acceleration are indistinguishable within a sufficiently local environment
- general theory of relativity
- Einstein’s theory relating gravity and the structure (geometry) of space and time


