1.6: The Equivalence Principle (Part 2)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Gravitational Red-shifts
Earlier, we saw experimental evidence that the rate of flow of time changes with height in a gravitational field. We can now see that this is required by the equivalence principle.
By the equivalence principle, there is no way to tell the difference between experimental results obtained in an accelerating laboratory and those found in a laboratory immersed in a gravitational field.30 In a laboratory accelerating upward, a photon emitted from the floor and would be Doppler-shifted toward lower frequencies when observed at the ceiling, because of the change in the receiver’s velocity during the photon’s time of flight. The effect is given by
ΔEE=Δff=ayc2
where a is the lab’s acceleration, y is the height from floor to ceiling, and c is the speed of light.
Note
Problem 4 verifies, in one specific example, that this way of stating the equivalence principle is implied by the one stated earlier.
Exercise 1.6.1
Self-check: Verify this statement.
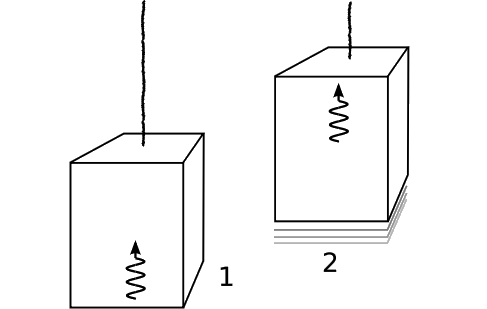
By the equivalence principle, we find that when such an experiment is done in a gravitational field g, there should be a gravitational effect on the energy of a photon equal to ΔEE=gyc2. Since the quantity gy is the gravitational potential (gravitational energy per unit mass), the photon’s fractional loss of energy is the same as the (Newtonian) loss of energy experienced by a material object of mass m and initial kinetic energy mc2.
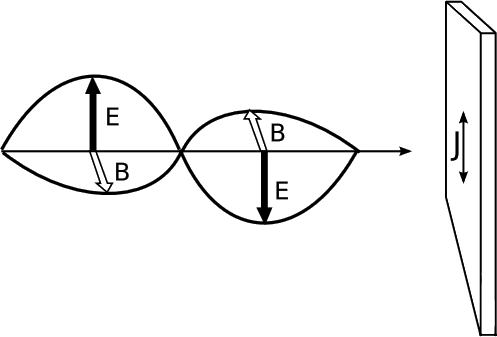
The interpretation is as follows. Classical electromagnetism requires that electromagnetic waves have inertia. For example, if a plane wave strikes an ohmic surface, as in Figure 1.5.14, the wave’s electric field excites oscillating currents in the surface. These currents then experience a magnetic force from the wave’s magnetic field, and application of the right-hand rule shows that the resulting force is in the direction of propagation of the wave. Thus the light wave acts as if it has momentum. The equivalence principle says that whatever has inertia must also participate in gravitational interactions. Therefore light waves must have weight, and must lose energy when they rise through a gravitational field.
Exercise 1.6.2
Self-check: Verify the application of the right-hand rule described above.
Further interpretation:
- The quantity mc2 is famous, even among people who don’t know what m and c stand for. This is the first hint of where it comes from. The full story is given in section 4.2.
- The relation p = Ec between the energy and momentum of a light wave follows directly from Maxwell’s equations, by the argument above; however, we will see in section 4.2 that according to relativity this relation must hold for any massless particle
- What we have found agrees with Niels Bohr’s correspondence principle, which states that when a new physical theory, such as relativity, replaces an older one, such as Newtonian physics, the new theory must agree with the old one under the experimental conditions in which the old theory had been verified by experiments. The gravitational mass of a beam of light with energy E is Ec2, and since c is a big number, it is not surprising that the weight of light rays had never been detected before Einstein trying to detect it.
- This book describes one particular theory of gravity, Einstein’s theory of general relativity. There are other theories of gravity, and some of these, such as the Brans-Dicke theory, do just as well as general relativity in agreeing with the presently available experimental data. Our prediction of gravitational Doppler shifts of light only depended on the equivalence principle, which is one ingredient of general relativity. Experimental tests of this prediction only test the equivalence principle; they do not allow us to distinguish between one theory of gravity and another if both theories incorporate the equivalence principle.
- If an object such as a radio transmitter or an atom in an excited state emits an electromagnetic wave with a frequency f, then the object can be considered to be a type of clock. We can therefore interpret the gravitational red-shift as a gravitational time dilation: a difference in the rate at which time itself flows, depending on the gravitational potential. This is consistent with the empirical results presented in Section 1.2.
Example 3: Chiao's paradox revisited
The equivalence principle says that electromagnetic waves have gravitational mass as well as inertial mass, so it seems clear that the same must hold for static fields. In Chiao’s paradox, the orbiting charged particle has an electric field that extends out to infinity. When we measure the mass of a charged particle such as an electron, there is no way to separate the mass of this field from a more localized contribution. The electric field “falls” through the gravitational field, and the equivalence principle, which is local, cannot guarantee that all parts of the field rotate uniformly about the earth, even in distant parts of the universe. The electric field pattern becomes distorted, and this distortion causes a radiation reaction which back-reacts on the particle, causing its orbit to decay.
The Pound-Rebka Experiment
The 1959 Pound-Rebka experiment at Harvard31 was one of the first high-precision, relativistic tests of the equivalence principle to be carried out under controlled conditions, and in this section we will discuss it in detail.
When y is on the order of magnitude of the height of a building, the value of ΔEE=gyc2 is ∼ 10−14, so an extremely high-precision experiment is necessary in order to detect a gravitational red-shift. A number of other effects are big enough to obscure it entirely, and must somehow be eliminated or compensated for. These are listed below, along with their orders of magnitude in the experimental design finally settled on by Pound and Rebka.
| (1) Classical Doppler broadening due to temperature. Thermal motion causes Doppler shifts of emitted photons, corresponding to the random component of the emitting atom’s velocity vector along the direction of emission. | ∼ 10−6 |
| (2) The recoil Doppler shift. When an atom emits a photon with energy E and momentum p=Ec, conservation of momentum requires that the atom recoil with momentum p=−Ec and energy p22m. This causes a downward Doppler shift of the energy of the emitted photon. A similar effect occurs on absorption, doubling the problem. | ∼ 10−12 |
| (3) Natural line width. The Heisenberg uncertainty principle says that a state with a half-life τ must have an uncertainty in its energy of at least ∼ hτ, where h is Planck’s constant. | ∼ 10−12 |
| (4) Special-relativistic Doppler shift due to temperature. Section 1.2 presented experimental evidence that time flows at a different rate depending on the motion of the observer. Therefore the thermal motion of an atom emitting a photon has an effect on the frequency of the photon, even if the atom’s motion is not along the line of emission. The equations needed in order to calculate this effect will not be derived until section 2.2; a quantitative estimate is given in example 13. For now, we only need to know that this leads to a temperature-dependence in the average frequency of emission, in addition to the broadening of the bell curve described by effect (1) above. | ∼ 10−14 per degree C |
The most straightforward way to mitigate effect (1) is to use photons emitted from a solid. At first glance this would seem like a bad idea, since electrons in a solid emit a continuous spectrum of light, not a discrete spectrum like the ones emitted by gases; this is because we have N electrons, where N is on the order of Avogadro’s number, all interacting strongly with one another, so by the correspondence principle the discrete quantum-mechanical behavior must be averaged out. But the protons and neutrons within one nucleus do not interact much at all with those in other nuclei, so the photons emitted by a nucleus do have a discrete spectrum. The energy scale of nuclear excitations is in the keV or MeV range, so these photons are x-rays or gamma-rays. Furthermore, the timescale of the random vibrations of a nucleus in a solid are extremely short. For a velocity on the order of 100 m/s, and vibrations with an amplitude of ∼ 10−10 m, the time is about 10−12 s. In many cases, this is much shorter than the half-life of the excited nuclear state emitting the gamma-ray, and therefore the Doppler shift averages out to nearly zero.
Effect (2) is still much bigger than the 10−14 size of the effect to be measured. It can be avoided by exploiting the Mössbauer effect, in which a nucleus in a solid substance at low temperature emits or absorbs a gamma-ray photon, but with significant probability the recoil is taken up not by the individual nucleus but by a vibration of the atomic lattice as a whole. Since the recoil energy varies as p22m, the large mass of the lattice leads to a very small dissipation of energy into the recoiling lattice. Thus if a photon is emitted and absorbed by identical nuclei in a solid, and for both emission and absorption the recoil momentum is taken up by the lattice as a whole, then there is a negligible energy shift. One must pick an isotope that emits photons with energies of about 10-100 keV. X-rays with energies lower than about 10 keV tend to be absorbed strongly by matter and are difficult to detect, whereas for gamma-ray energies ≳ 100 keV the M¨ossbauer effect is not sufficient to eliminate the recoil effect completely enough.
If the Mössbauer effect is carried out in a horizontal plane, resonant absorption occurs. When the source and absorber are aligned vertically, p, gravitational frequency shifts should cause a mismatch, destroying the resonance. One can move the source at a small velocity (typically a few mm/s) in order to add a Doppler shift onto the frequency; by determining the velocity that compensates for the gravitational effect, one can determine how big the gravitational effect is.
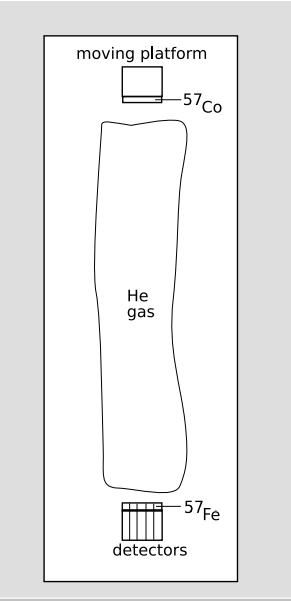
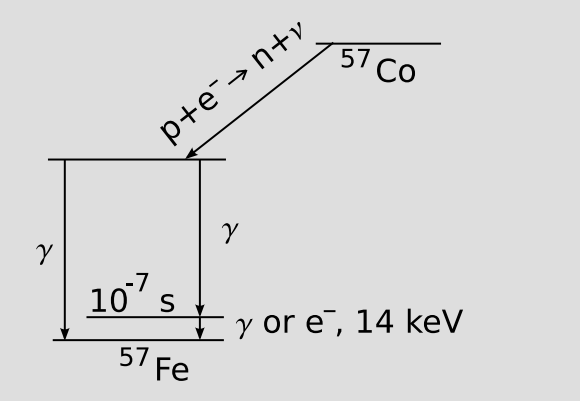
The typical half-life for deexcitation of a nucleus by emission of a gamma-ray with energy E is in the nanosecond range. To measure an gravitational effect at the 10−14 level, one would like to have a natural line width, (3), with ΔEE ≲ 10−14, which would require a half-life of ≳ 10 μs. In practice, Pound and Rebka found that other effects, such as (4) and electron-nucleus interactions that depended on the preparation of the sample, tended to put nuclei in one sample “out of tune” with those in another sample at the 10−13-10−12 level, so that resonance could not be achieved unless the natural line width gave ΔEE≳ 10−12. As a result, they settled on an experiment in which 14 keV gammas were emitted by 57Fe nuclei (Figure 1.5.17) at the top of a 22-meter tower, and absorbed by 57Fe nuclei at the bottom. The 100-ns half-life of the excited state leads to ΔEE ∼ 10−12. This is 500 times greater than the gravitational effect to be measured, so, as described in more detail below, the experiment depended on high-precision measurements of small up-and-down shifts of the bell-shaped resonance curve.
The absorbers were seven iron films isotopically enhanced in 57Fe, applied directly to the faces of seven sodium-iodide scintillation detectors (bottom of Figure 1.5.16). When a gamma-ray impinges on the absorbers, a number of different things can happen, of which we can get away with considering only the following: (a) the gamma-ray is resonantly absorbed in one of the 57Fe absorbers, after which the excited nucleus decays by re-emission of another such photon (or a conversion electron), in a random direction; (b) the gamma-ray passes through the absorber and then produces ionization directly in the sodium iodide crystal. In case b, the gamma-ray is detected. In case a, there is a 50% probability that the re-emitted photon will come out in the upward direction, so that it cannot be detected. Thus when the conditions are right for resonance, a reduction in count rate is expected. The M¨ossbauer effect never occurs with 100% probability; in this experiment, about a third of the gammas incident on the absorbers were resonantly absorbed.
The choice of y = 22 m was dictated mainly by systematic errors. The experiment was limited by the strength of the gamma-ray source. For a source of a fixed strength, the count rate in the detector at a distance y would be proportional to y−2, leading to statistical errors proportional to 1/√countrate∝y. Since the effect to be measured is also proportional to y, the signal-to-noise ratio was independent of y. However, systematic effects such as (4) were easier to monitor and account for when y was fairly large. A lab building at Harvard happened to have a 22-meter tower, which was used for the experiment. To reduce the absorption of the gammas in the 22 meters of air, a long, cylindrical mylar bag full of helium gas was placed in the shaft, p.
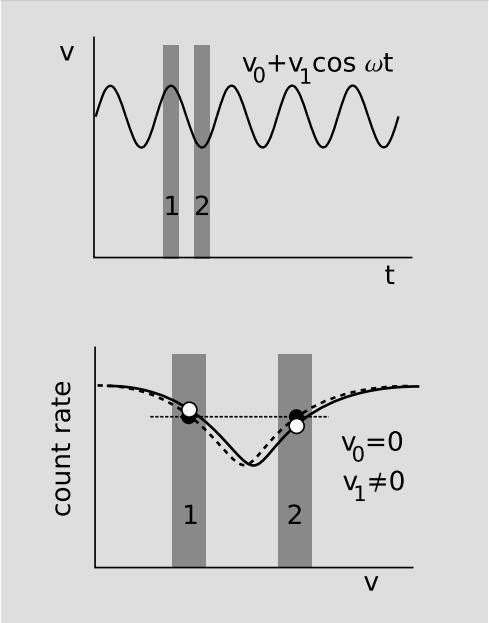
The resonance was a bell-shaped curve with a minimum at the natural frequency of emission. Since the curve was at a minimum, where its derivative was zero, the sensitivity of the count rate to the gravitational shift would have been nearly zero if the source had been stationary. Therefore it was necessary to vibrate the source up and down, so that the emitted photons would be Doppler shifted onto the shoulders of the resonance curve, where the slope of the curve was large. The resulting asymmetry in count rates is shown in Figure 1.5.18. A further effort to cancel out possible systematic effects was made by frequently swapping the source and absorber between the top and bottom of the tower.
For y = 22.6 m, the equivalence principle predicts a fractional frequency shift due to gravity of 2.46 × 10−15. Pound and Rebka measured the shift to be (2.56 ± 0.25) × 10−15. The results were in statistical agreement with theory, and verified the predicted size of the effect to a precision of 10%.

Figure 1.6.19 - Pound and Rebka at the top and bottom of the tower.
References
31 Phys. Rev. Lett. 4 (1960) 337


