14.3: The Parabola

The parabola can be defines as the limiting curve of an ellipse as one focus (in the case we’re examining, that would be $\left.F_{1}\right)$ going to infinity. The eccentricity evidently goes to one, $e \rightarrow 1$ since the center of the ellipse has gone to infinity as well. The semi-latus rectum $ℓ$ is still defined as the perpendicular distance from the focus to the curve, the equation is

$$\ell=r(1+\cos \theta)$$

Note that this describes a parabola opening to the left. Taking $OF=1$, the equation of this parabola is $y^{2}=-4 x$.

Figure $\PageIndex{1}$

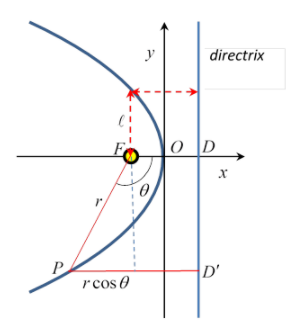
All parabolas look the same, apart from scaling (maybe just in one direction). The line perpendicular to the axis and the same distance from the curve along the axis as the focus is, but outside the curve, is the parabola’s directrix. That is, $FO=OD$.

Each point on the curve is the same distance from the focus as it is from the directrix. This can be deduced from the limit of the ellipse property that the sum of distances to the two foci is constant. Let’s call the other focus $\infty$. Then $F P+P \infty=F O+O \infty=D \infty=D^{\prime} \infty$. So from the diagram, $F P=P D^{\prime}$

Exercise $\PageIndex{1}$

Prove by finding the slope, etc., that any ray of light emitted by a point lamp at the focus will be reflected by a parabolic mirror to go out parallel to the axis.

Exercise $\PageIndex{1}$

From the diagram above, show that the equality $F P=P D^{\prime}$ easily gives the equation for the parabola, both in (r,θ) and in (x,y) coordinates.