5.4.6: Rods
( \newcommand{\kernel}{\mathrm{null}\,}\)
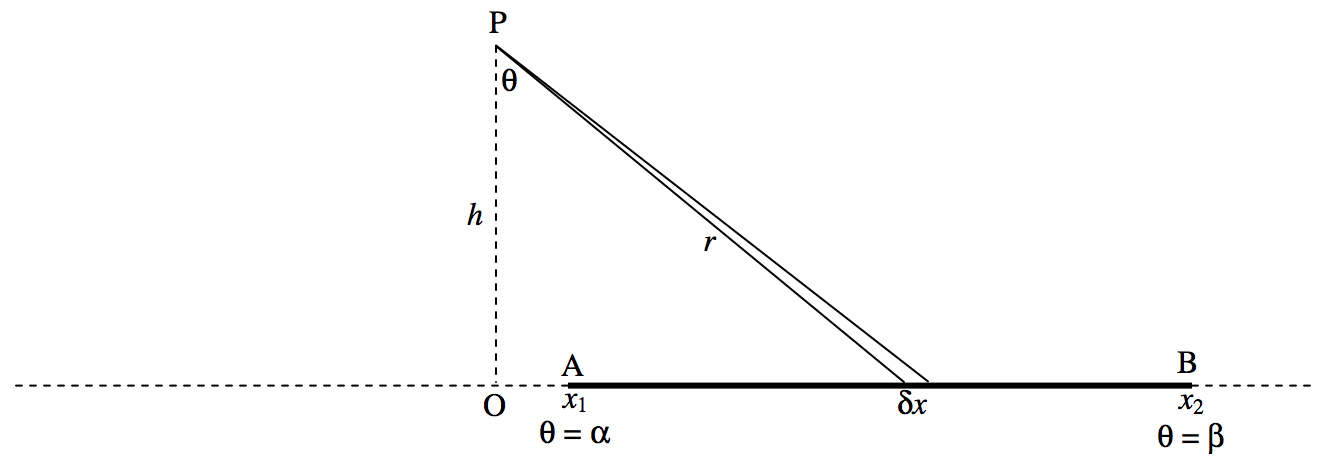
FIGURE V.5
Consider the rod shown in figure V.5, of mass per unit length λ. The field at \text{P} due to the element δx is Gλ δx/r^2. But x = \tan θ, δx = h \sec^2 θδθ, r = h \sec θ so the field at \text{P} is Gλ δθ / h This is directed from \text{P} to the element δx.
The x-component of the field due to the whole rod is
\frac{Gλ}{h} \int_α^β \sin θ \ dθ = \frac{Gλ}{h} ( \cos α - \cos β ). \label{5.4.15} \tag{5.4.15}
The y-component of the field due to the whole rod is
-\frac{Gλ}{h} \int_α^β \cos θ \ dθ = -\frac{Gλ}{h} ( \sin β - \sin α). \label{5.4.16} \tag{5.4.16}
The total field is the orthogonal sum of these, which, after use of some trigonometric identities (do it!), becomes
g = \frac{2Gλ}{h} \sin \frac{1}{2} (β - α) \label{5.4.17} \tag{5.4.17}
at an angle \frac{1}{2} (α + β) - i.e. bisecting the angle \text{APB}.
If the rod is of infinite length, we put α = − \pi/2 and β = \pi /2, and we obtain for the field at \text{P}
g = \frac{2Gλ}{h}. \label{5.4.18} \tag{5.4.18}
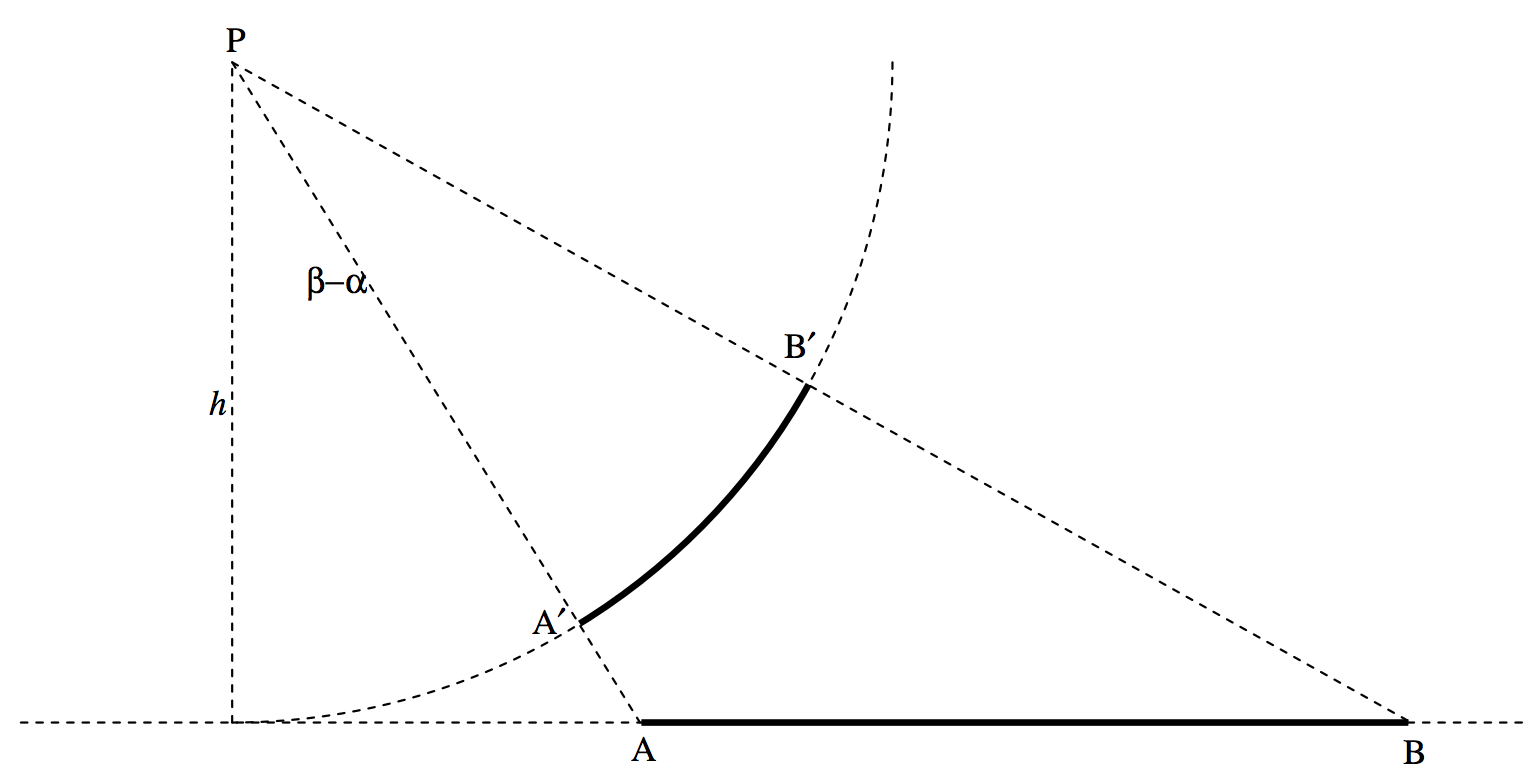
text{FIGURE V.6}
Consider an arc \text{A}^\prime \text{B}^\prime of a circle of radius h, mass per unit length λ, subtending an angle β−α at the centre \text{P} of the circle.
Exercise: Show that the field at \text{P} is g = \frac{2Gλ}{h} \sin \frac{1}{2}(β−α). This is the same as the field due to the rod \text{AB} subtending the same angle. If \text{A}^\prime \text{B}^\prime is a semicircle, the field at \text{P} would be g = \frac{2Gλ}{h}, the same as for an infinite rod.
An interesting result following from this is as follows.
\text{FIGURE V.7}
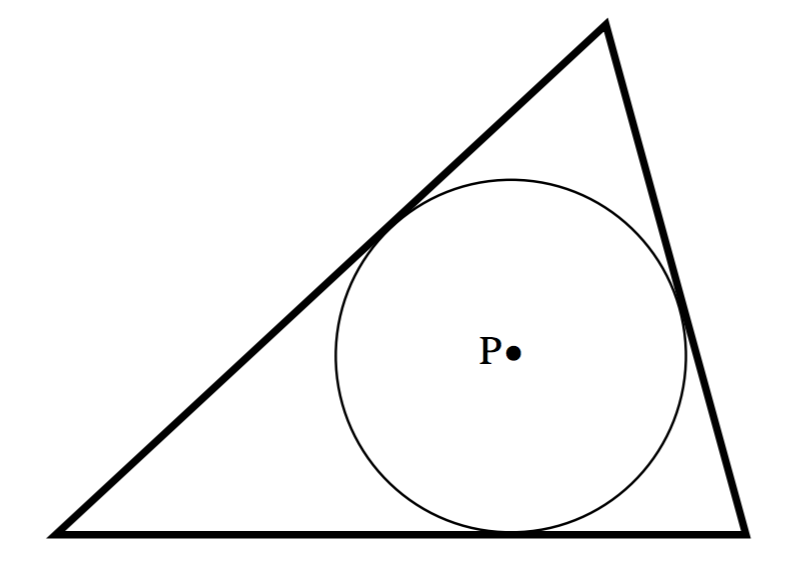
Three massive rods form a triangle. \text{P} is the incentre of the triangle (i.e. it is equidistant from all three sides.) The field at \text{P} is the same as that which would be obtained if the mass were distributed around the incircle. I.e., it is zero. The same result would hold for any quadrilateral that can be inscribed with a circle – such as a cyclic quadrilateral.


