5.4.7: Solid Cylinder
- Page ID
- 8137
We do this not because it has any particular relevance to celestial mechanics, but because it is easy to do. We imagine a solid cylinder, density \(ρ\), radius \(a\), length \(l\). We seek to calculate the field at a point \(\text{P}\) on the axis, at a distance \(h\) from one end of the cylinder (figure \(\text{V.8}\)).
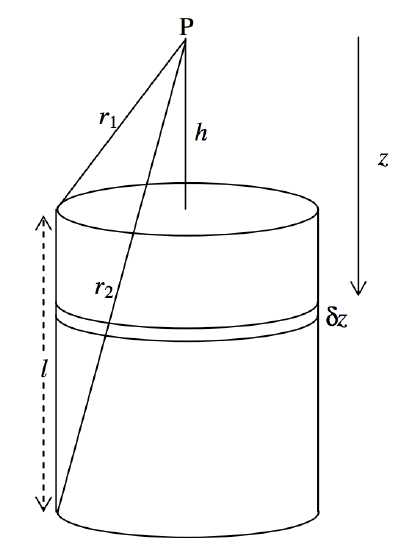
\(\text{FIGURE V.8}\)
The field at \(\text{P}\) from an elemental disc of thickness \(δz\) a distance z below P is (from Equation 5.4.9)
\[δg = Gρδzω. \label{5.4.19} \tag{5.4.19}\]
Here \(ω\) is the solid angle subtended at \(\text{P}\) by the disc, which is \(2 \pi \left[ 1 - \frac{z}{\left( z^2 + a^2 \right)^{1/2}} \right]\). Thus the field at \(\text{P}\) from the entire cylinder is
\[g = 2 \pi G ρ \int_h^{l+h} \left[ 1 - \frac{z}{(z^2 + a^2)^{1/2}} \right] dz, \label{5.4.20} \tag{5.4.20}\]
or \[g = 2 \pi G ρ \left( l - \sqrt{(l+h)^2 + a^2} + \sqrt{h^2+ a^2} \right), \label{5.4.21} \tag{5.4.21}\]
or \[g = 2\pi G ρ ( l - r_2 + r_1 ). \label{5.4.22} \tag{5.4.22}\]
It might also be of interest to express \(g\) in terms of the height \(y (= \frac{1}{2}l + h)\) of the point \(\text{P}\) above the mid-point of the cylinder. Instead of Equation \(\ref{5.4.21}\), we then have
\[g = 2 \pi G ρ \left( l - \sqrt{(y + \frac{1}{2}l)^2 + a^2} + \sqrt{(y - \frac{1}{2}l)^2 + a^2} \right) . \label{5.4.23} \tag{5.4.23}\]
If the point \(\text{P}\) is inside the cylinder,at a distance \(h\) below the upper end of the cylinder, the limits of integration in Equation \(\ref{5.4.20}\) are \(h\) and \(l − h\), and the distance \(y\) is \(\frac{1}{2}l − h\). In terms of \(y\) the gravitational field at \(\text{P}\) is then
\[g = 2 \pi G ρ \left( 2y - \sqrt{(y + \frac{1}{2}l)^2 + a^2} + \sqrt{(y-\frac{1}{2}l)^2 + a^2} \right). \label{5.4.24} \tag{5.4.24}\]
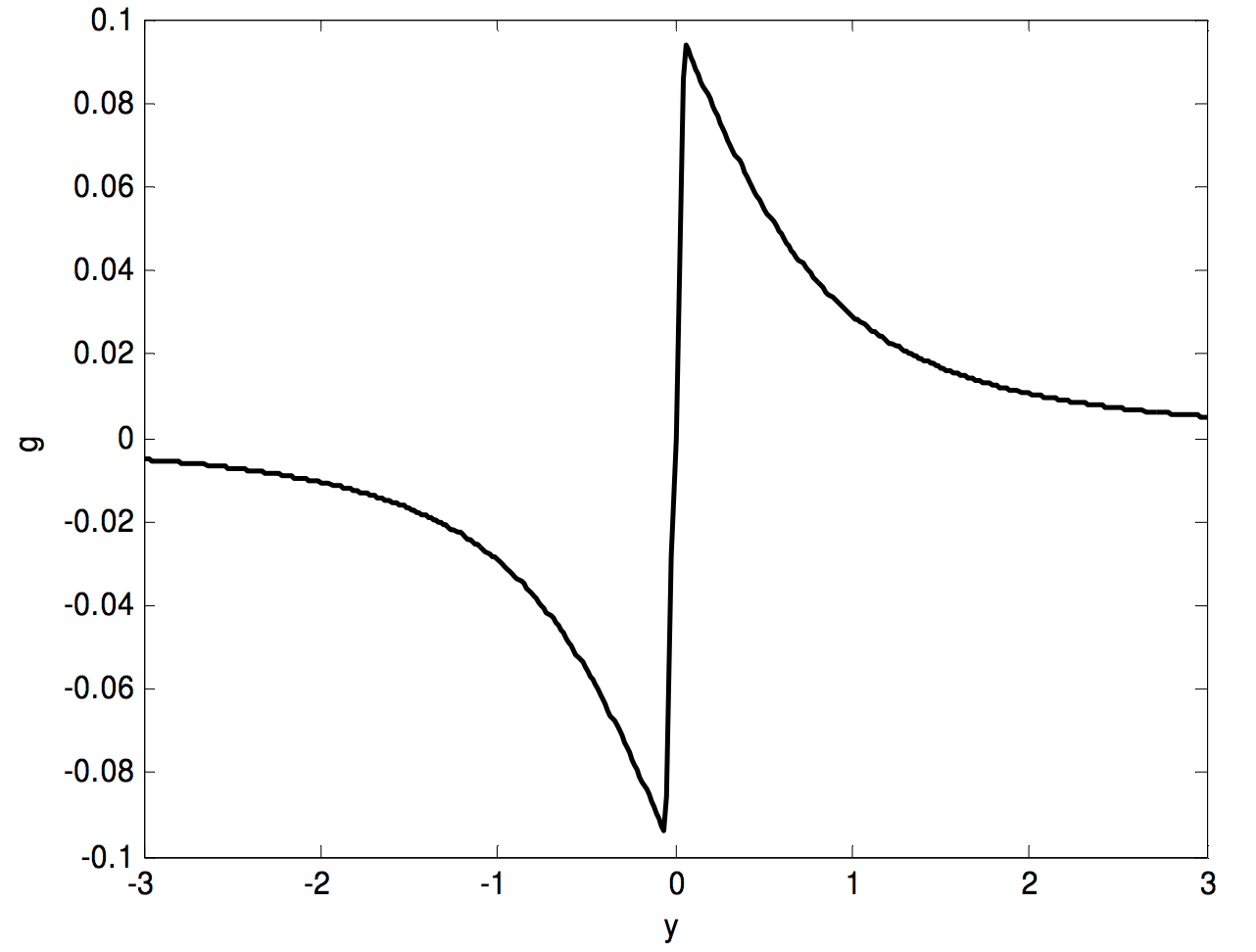
In the graph below I have assumed, by way of example, that \(l\) and \(a\) are both 1, and I have plotted \(g\) in units of \(2 \pi Gρ\) (counting \(g\) as positive when it is directed downwards) from \(y = −1\) to \(y = + 1\). The portion inside the cylinder \((- \frac{1}{2} ≤ y ≤ \frac{1}{2}l)\), represented by Equation \(\ref{5.4.24}\), is almost, but not quite, linear. The field at the centre of the cylinder is, of course, zero.
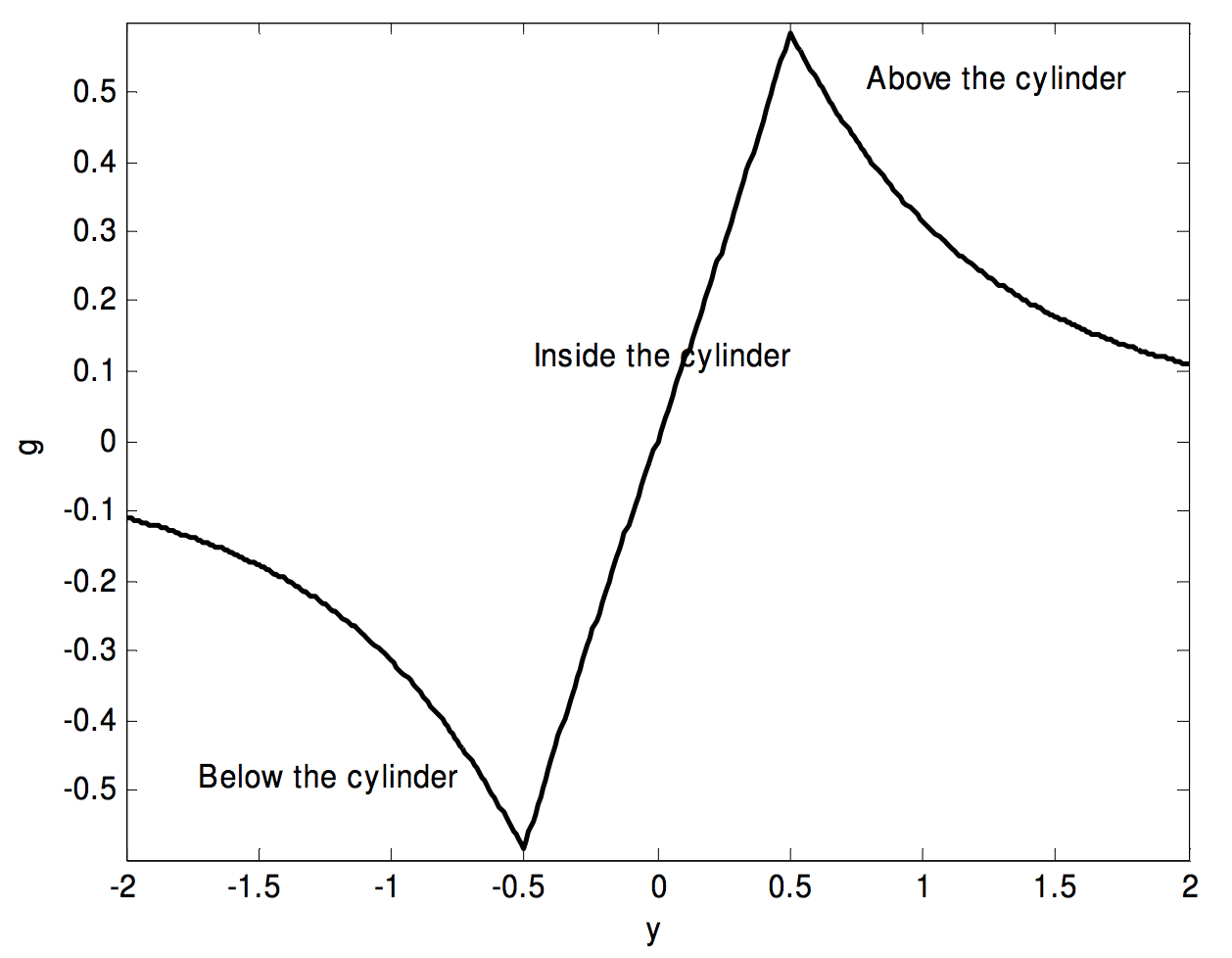
Below, I draw the same graph, but for a thin disc, with \(a = 1\) and \(l = 0.1\). We see how it is that the field reaches a maximum immediately above or below the disc, but is zero at the centre of the disc.