5.4.8: Hollow Spherical Shell
( \newcommand{\kernel}{\mathrm{null}\,}\)
We imagine a hollow spherical shell of radius a, surface density σ, and a point \text{P} at a distance r from the centre of the sphere. Consider an elemental zone of thickness δx. The mass of this element is 2πaσ \ δx. (In case you doubt this, or you didn’t know, “the area of a zone on the surface of a sphere is equal to the corresponding area projected on to the circumscribing cylinder”.)
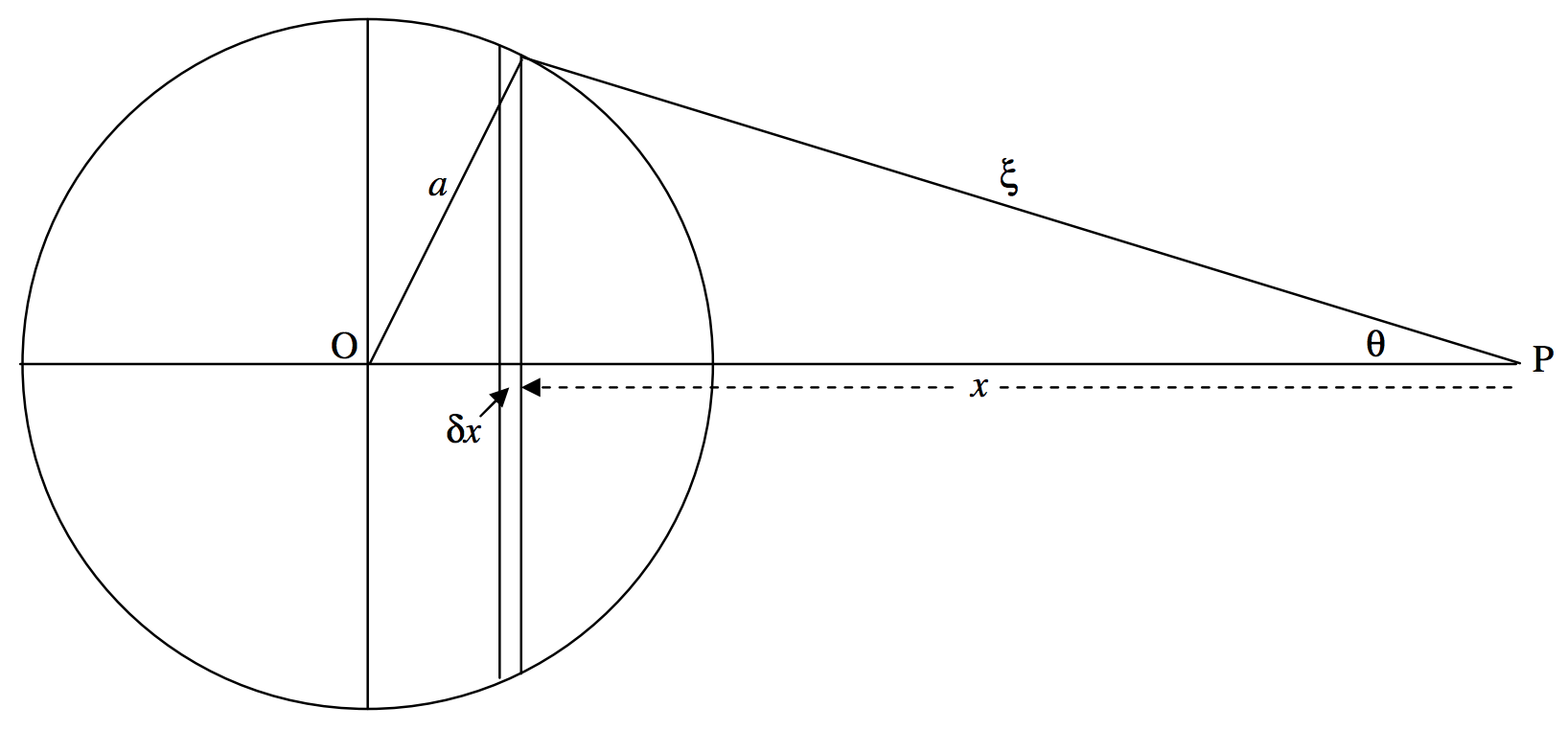
\text{FIGURE V.9}
The field due to this zone, in the direction \text{PO} is
\frac{2 πaσG \cos θδx}{ξ^2}.
Let’s express this all in terms of a single variable, ξ. We are going to have to express x and θ in terms of ξ.
We have
a^2 = r^2 + ξ^2 - 2rξ \cos θ = r^2 + ξ^2 - 2rx,
from which
\cos θ = \frac{r^2 - a^2 + ξ^2}{2rξ} \quad δx = \frac{ξδξ}{r}.
Therefore the field at \text{P} due to the zone is \frac{\pi a G σ}{r^2} \left( 1 + \frac{r^2 - a^2}{ξ^2} \right) δξ.
If \text{P} is an external point, in order to find the field due to the entire spherical shell, we integrate from ξ = r − a to r + a. This results in
g = \frac{GM}{r^2} . \label{5.4.23}
However, if \text{P} is an internal point, in order to find the field due to the entire spherical shell, we integrate from ξ = a − r to a + r, which results in g = 0.
Thus we have the important result that the field at an external point due to a hollow spherical shell is exactly the same as if all the mass were concentrated at a point at the centre of the sphere, whereas the field inside the sphere is zero.
Caution. The field inside the sphere is zero only if there are no other masses present. The hollow sphere will not shield you from the gravitational field of any other masses that might be present. Thus in figure V.10, the field at \text{P} is the sum of the field due to the hollow sphere (which is indeed zero) and the field of the mass M, which is not zero. Anti-grav is a useful device in science fiction, but does not occur in science fact.
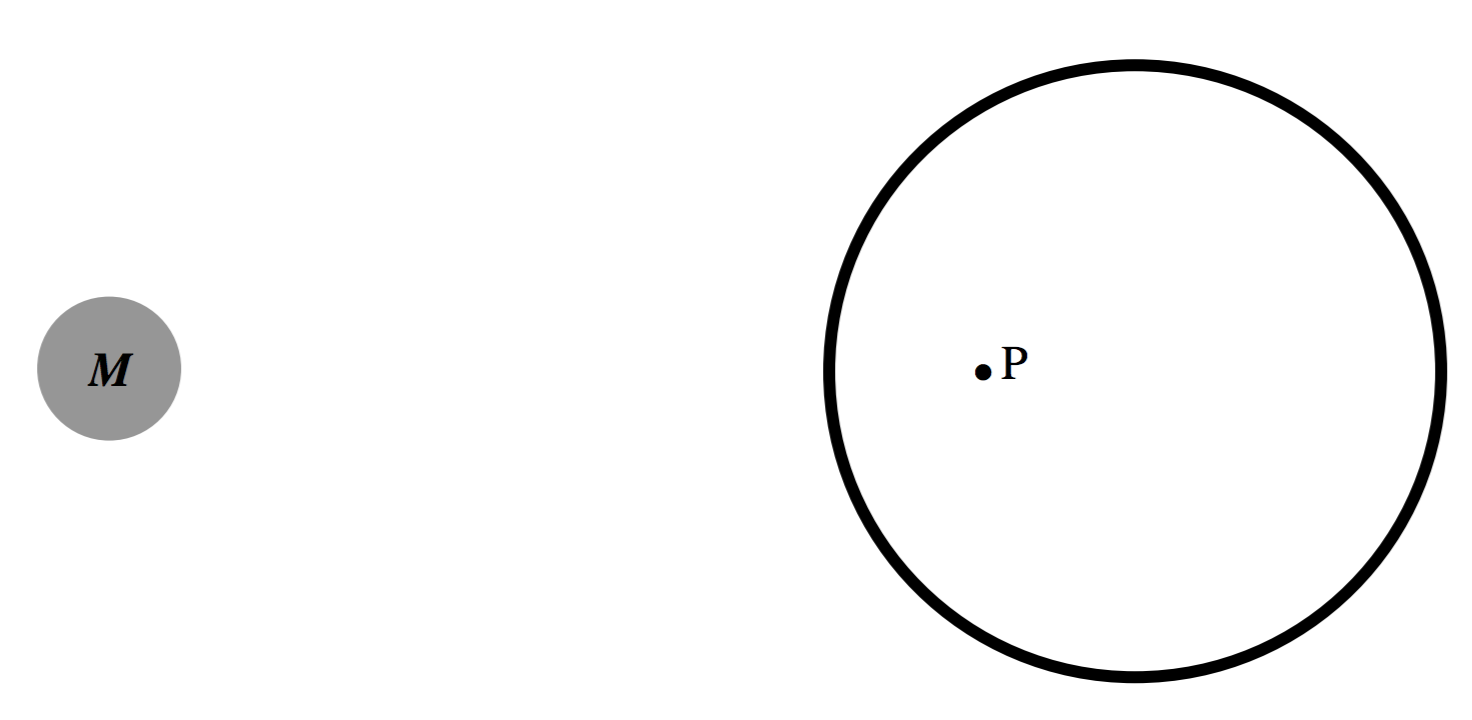
\text{FIGURE V.10}


