6.7: Precession

The First Point of Aries is the point where the ecliptic crosses the equator at the point occupied by the Sun at the March equinox. It is the point from which right ascensions are measured. We have hitherto treated it as if it were fixed relative to the stars, although we have hinted from time to time that this is not exactly so. Indeed we have said that it is essential, when stating the right ascension and declination of a star, to state the date of the equinox to which it refers.

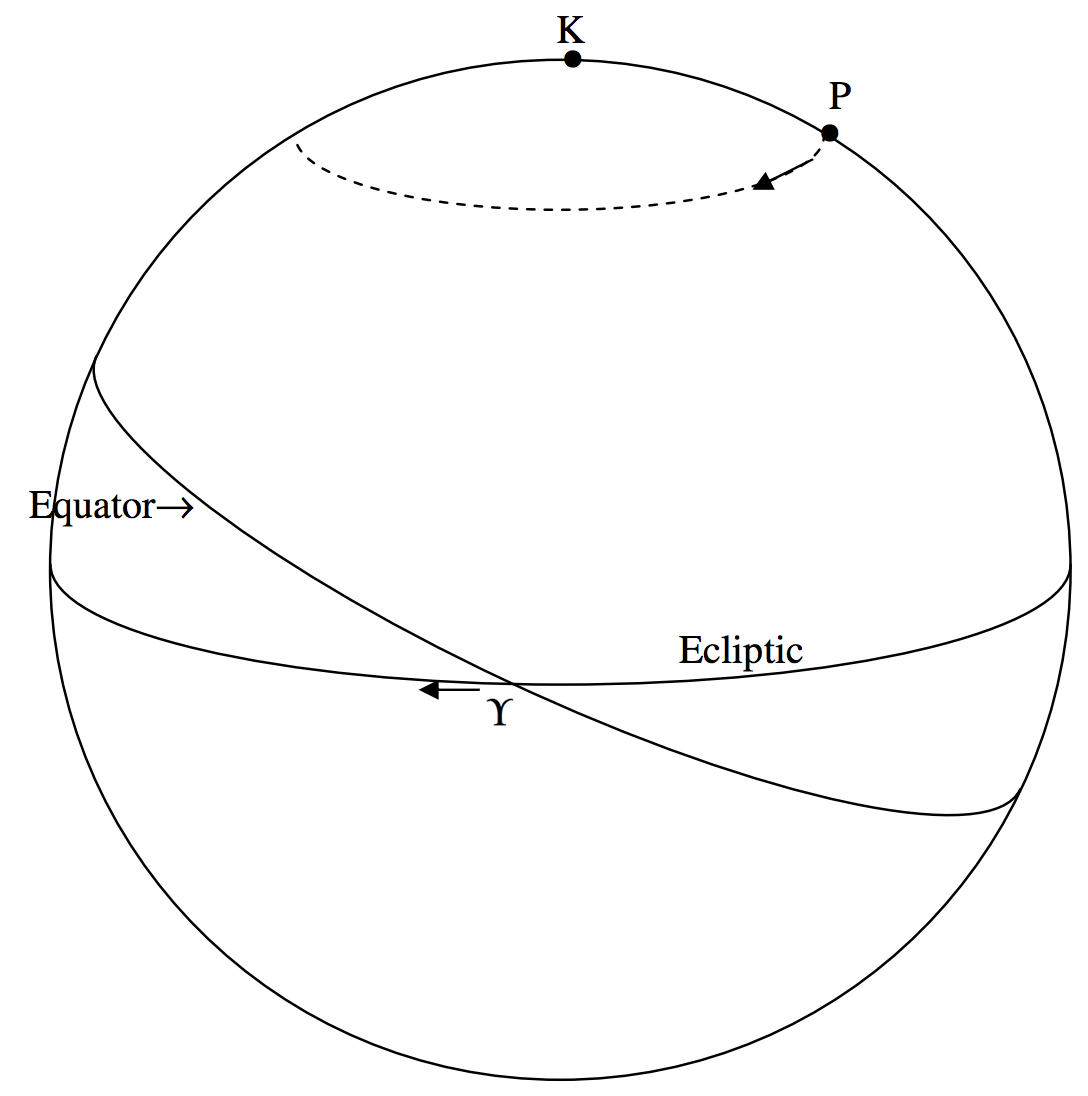
In figure \(\text{VI.6}\), I have drawn the ecliptic horizontally, and the celestial equator inclined at an angle of \(23^\circ .4\). You can see the north pole of the ecliptic, \(\text{K}\), and the north celestial pole \(\text{P}\). The great circle \(\text{P} \Upsilon\) (not drawn) is the equinoctial colure, and the right ascension of \(\Upsilon\) is \(0^h\). The right ascension and declination of \(\text{K}\) are \(18^h\), \(+66^\circ .6\), which is a point between the stars \(δ\) and \(ζ\) Draconis.

Neither the north celestial pole \(\text{P}\) nor the “First Point of Aries” \(\Upsilon\) are fixed, however. The north celestial pole \(\text{P}\) describes a small circle of radius \(23^\circ .4\) around \(\text{K}\), and the equinox regresses westwards along the ecliptic in a period of 25,800 years. This motion, called the precession of the equinoxes (or just “precession” for short) is not quite uniform, but is nearly so and will be treated as such in this section. The complete cycle of 25,800 years corresponds to a westward regression of \(\Upsilon\) along the ecliptic of \(50^{\prime \prime}.2\) per year or \(0^{\prime \prime}.137\) per day. The component of that motion along the celestial equator is \(0^{\prime \prime}.137\) \(\cos 23^\circ .4 = 0^{\prime \prime} .126 = 0^{\text{s}} .008\) per day. That is why the length of the mean sidereal day (which is defined as the interval between two consecutive upper meridian transits of the first point of Aries) is \(0^{\text{s}} .008\) shorter than the sidereal rotation period of Earth.

The precession of \(\text{P}\) around \(\text{K}\) means that the entire system of equatorial coordinates (right ascension and declination) moves continuously, and the right ascensions and declinations of all the stars are continuously changing. No matter where \(\text{P}\) is in its journey around \(\text{K}\), however, the equatorial coordinates of \(\Upsilon\) and of \(\text{K}\) are always \(0^{\text{h}}\), \(0^{\text{o}}\) and \(18^\text{h}\), \(+66^\text{o} .5\). However, equatorial coordinates of the stars must always be referred to the equinox and equator of a stated epoch.

\(\text{FIGURE VI.6}\)

During much of the twentieth century, the epoch referred to by many catalogues and atlases was \(\text{B}1950.0\). That is the beginning of the Besselian Year of 1950, at the instant (shortly before midnight on the night of 1949 Dec 31 / 1950 Jan 1) when the right ascension of the Mean Sun was \(18^\text{h} 40^\text{m}\). Most catalogues since 1984 have referred right ascensions and declinations to the mean equinox and equator of \(\text{J}2000.0\). That is the beginning of the Julian Year 2000, at the instant when Greenwich Mean Time (UT) indicated midnight. For example, in the older catalogues, the right ascension and declination of Arcturus would be given as

\[α_{1950.0} = 14^\text{h} \quad 13^\text{m}.4 \quad δ_{1950.0} = +19^\circ 26^\prime,\]

whereas in more recent catalogues they are given as

\[α_{2000.0} = 14^\text{h} \quad 15^\text{m}.8 \quad δ_{2000.0} = +19^\circ 11^\prime . \]

Thus it can be seen that for precise work the difference is not at all negligible, and to state the equatorial coordinates of an object without also stating the epoch of the equinox and equator to which the coordinates are referred is not generally useful. Of course, when setting the circles of a telescope for the night’s observations, what one needs are the right ascension and declination referred to the equinox and equator of date – i.e. for the date in question. It is therefore essential for a practical observer to know how to correct for precession.

\(\text{FIGURE VI.7}\)

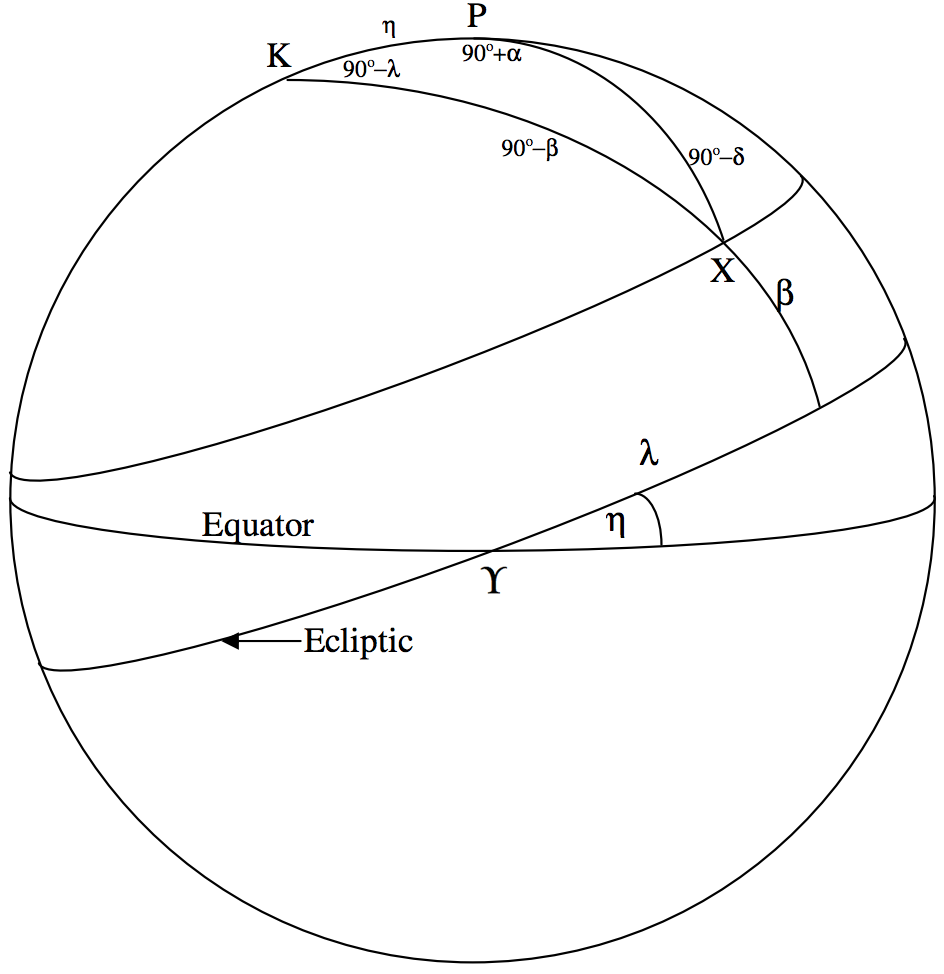
Apply the cosine formula (Equation 3.5.2) to triangle \(\text{PKX}\) to obtain

\[\sin δ = \cos η \sin β + \sin η \cos β \sin λ. \label{6.7.1} \tag{6.7.1}\]

Since \(\Upsilon\) is regressing down the ecliptic, the ecliptic longitude \(λ\) of the star \(\text{X}\) is increasing. If it is increasing at a rate \(\dot{λ}\) \((= 50^{\prime \prime}.2\) per year), the rate of change of its declination can be obtained by differentiation of Equation \(\ref{6.7.1}\) with respect to time, bearing in mind that \(β\) and \(η\) are constant:

\[\cos δ \dot{δ} = \sin η \cos β \cos λ \dot{λ} . \label{6.7.2} \tag{6.7.2}\]

But \((\cos β \cos λ)/\cosδ\) is obtained from the sine formula (Equation 3.5.1):

\[\frac{\cos β}{\cos α} = \frac{\cos δ}{\cos λ} . \label{6.7.3} \tag{6.7.3}\]

Hence we obtain for the rate of change of declination of a star due to precession:

\[\dot{δ} = \dot{λ} \sin η \cos α . \label{6.7.4} \tag{6.7.4}\]

To obtain the rate of change of right ascension, we can write Equation \(\ref{6.7.3}\) as

\[\cos α = \cos β \sec δ \cos λ \label{6.7.5} \tag{6.7.5}\]

and then differentiate with respect to time:

\[-\sin α \dot{α} = \cos β \sec δ (\tan δ \dot{δ} \cos λ - \sin λ \dot{λ}), \label{6.7.6} \tag{6.7.6}\]

which I am going to write as

\[-\sin α \dot{α} = \cos β \sec δ \cos λ ( \tan δ \dot{δ} - \tan λ \dot{λ}). \label{6.7.7} \tag{6.7.7}\]

We can get \(\cos β \sec δ \cos λ\) from Equation \(\ref{6.7.5}\), and of course we have \(δ\) from Equation \(\ref{6.7.4}\), but we still need to find an expression for \(\tan λ\) in terms of equatorial coordinates. We can do this from the cotangent formula (Equation 3.5.4), in which the inner angle is \(90^\circ + α\) and the inner side is \(η\):

\[-\cos η \sin α = \sin η \tan δ - \cos α \tan λ . \label{6.7.8} \tag{6.7.8}\]

On substitution of Equations \ref{6.7.4}, \ref{6.7.5} and \ref{6.7.8} into Equation \ref{6.7.7} we obtain, after a very small amount of algebra, for the rate of change of right ascension of a star due to precession:

\[\dot{α} = \dot{λ} ( \cos η + \sin α \tan δ \sin η). \label{6.7.9} \tag{6.7.9}\]

With \(\dot{λ} = 50^{\prime \prime}.2\) per year and \(η = 23^\circ .4\), Equations \ref{6.7.4} and \ref{6.7.9} become

\[\dot{δ} = 19^{\prime \prime} .9 \cos α \quad \text{per year} \label{6.7.10} \tag{6.7.10}\]

and \[\dot{α} = 46^{\prime \prime} .1 + 19^{\prime \prime} .9 \sin α \tan δ \quad \text{per year} \label{6.7.11} \tag{6.7.11}\]

or \[\dot{α} = 3^{s} .07 + 1^{\text{s}} .33 \sin α \tan δ \quad \text{per year}. \label{6.7.12} \tag{6.7.12}\]

These formulae should be adequate for all but very precise calculations.

Problem: Use Equations \ref{6.7.10} and \ref{6.7.12} to verify the data about Arcturus – and please let me know if it isn’t right!

At the time of Hipparcos (who discovered the phenomenon of precession as long ago as the second century B.C.), the spring equinox was in the constellation Aries – indeed at its eastern boundary. Hence it was called the First Point of Aries. Over the centuries, precession has carried the equinox westward right across the constellation Aries, and because of this, together with the way in which the constellation boundaries were formally fixed in 1928, the equinox is now near the western boundary of Pisces and is only a few degrees from Aquarius. It is still called, however, by its traditional name of the First Point of Aries. Incidentally, the ecliptic actually passes through the constellation Ophiuchus, which is not one of the traditional twelve “Signs of the Zodiac”, and it is sometimes said that this is a result of precession over the centuries. This is not the case. Precession does not alter the plane of the ecliptic, and the ecliptic continues to pass through the same constellations regardless of where the equinox is along it. The inclusion of Ophiuchus is merely a result of the way in which the constellation boundaries were formally fixed in 1928.

The Physical Cause of the Precession

The daily motion of the stars around the north celestial pole is, of course, a reflection of Earth’s rotation on its axis; and the annual motion of the Sun along the ecliptic, which is inclined at \(23^\circ .4\) to the celestial equator, is a reflection of the annual orbital motion of Earth around the Sun, the plane of Earth’s rotational equator being inclined at \(23^\circ .4\) to the plane of its orbit – i.e. to the ecliptic. Although this obliquity of \(23^\circ .4\) is approximately constant, the direction of Earth’s rotational axis is not fixed, but it precesses around the normal to the ecliptic plane with a period of 25,800 years.

From the point of view of classical mechanics, Earth is an oblate symmetric top. That is to say, it has an axis of symmetry and two of its principal moments of inertia are equal and are less than the moment of inertia about the axis of symmetry. The phenomena of precession of such a body are well understood and are studied in courses of classical mechanics. It is necessary, however, to be clear in one’s mind about the distinction between torque-free precession and torque-induced precession.

The phenomenon of torque-free precession is the precession that occurs when a symmetric top is spinning about an axis that does not coincide with its symmetry axis and it is spinning freely with no external torques acting upon it. In such circumstances, the angular momentum vector is fixed in magnitude and direction. The symmetry axis precesses about the fixed angular momentum vector while the instantaneous axis of rotation precesses about the symmetry axis. The rotation of Earth does indeed exhibit this type of behaviour, but this is not the precession that we are talking about in connection with the precession of the equinoxes. The instantaneous axis of rotation of Earth is only a very few metres away from its symmetry axis and the period of the torque-free precession is about 432 days. This gives rise to a phenomenon known as variation of latitude, and it results in the latitudes of locations of Earth’s surface varying quasi-periodically with an amplitude of less than a fifth of an arcsecond. The precession of the equinoxes that we have been discussing in this section is something entirely different.

The figure of Earth is approximately an oblate spheroid. If we call the equatorial radius \(a\) and the polar radius \(c\), the geometric ellipticity \((a − c)/ a\) is about \(1/297.0\). If we call the corresponding principal moments of inertia \(A\) and \(C\), the dynamical ellipticity \((C − A)/ A\) is about \(1/305.1\). Earth’s equator is inclined to the ecliptic, and, because of the equatorial bulge, the spinning Earth is subject to torques from both the Sun and the Moon (whose orbit is inclined to the ecliptic by about 5 degrees). The magnitude of the torque is proportional to the diameter of Earth times the gravitational field gradient \(2GM/r^3\), and the direction of the torque vector is perpendicular to the angular momentum vector.

Exercise \(\PageIndex{1}\)

Look up the masses of Sun and Moon, and their mean distances from Earth. Show that \(M/r^3\) for the Moon is about twice that for the Sun. Thus the torque on Earth exerted by the Moon is about twice the torque exerted by the Sun.

Now if a symmetric top is spinning about its axis of symmetry with angular momentum \(\textbf{L}\) and if it is subject to an external torque \(\boldsymbol{\tau}\), its angular momentum will change (not in magnitude, but in direction), and \(\textbf{L}\) will precess with an angular velocity \(\boldsymbol{\Omega}\) given by

\[\boldsymbol{\tau} = \boldsymbol{\Omega} \times \textbf{L}. \label{6.7.13} \tag{6.7.13}\]

Equation \ref{6.7.13} does not give the direction of \(\boldsymbol{\Omega}\) uniquely – that depends on the initial conditions. Figure \(\text{VI.8}\) illustrates the situation.

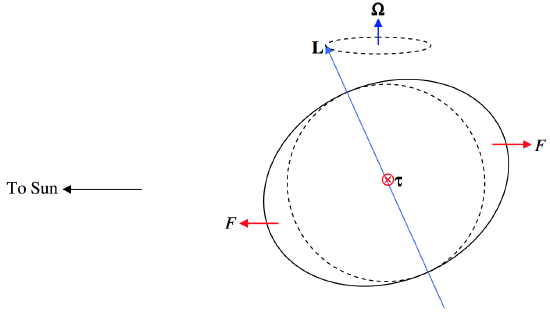
\(\text{FIGURE VI.8}\)

The equatorial bulge is much exaggerated. The figure is drawn in a reference frame that is revolving around the Sun with the Earth, so there is no net gravitational force on Earth (the gravitational attraction of the Sun is counteracted by the centrifugal force). In this frame, there is a little force \(F\) acting towards the Sun on the sunward-facing bulge, and an equal force acting away from the Sun on the opposite side. This amounts to a torque of magnitude \(\tau = Fd \sin η\), where \(η\) is the obliquity of the ecliptic and \(d\) is the diameter of Earth. Thus if we equate the magnitudes of both sides of Equation \ref{6.7.13}, we obtain for the angular speed of the precession

\[\Omega = Fd / L , \label{6.7.14} \tag{6.7.14}\]

which is independent of \(η\). This, then is the cause of the precession of the equinoxes, except that, for the purpose of figure \(\text{VI.8}\), I referred only to the Sun. You have yourself calculated that the influence of the Moon is about twice that of the Sun, and the combined effect of the Moon and the Sun is called the luni-solar precession. There is a small additional precession resulting from the influence of the other planets in the solar system.