7.22: Paschen-Back Effect

The description I have given so far of the way in which a level is split up and the states are separated in a magnetic field is good for relatively weak magnetic fields, but begins to break down for strong fields. What do I mean by "weak" and "strong"? The type of splitting I have described starts to break down when the energy separation of the states of a level becomes comparable to the separation of the levels within a multiplet. Stated otherwise, it breaks down when the strength of the coupling between \(\textbf{J}\) and \(\textbf{B}\) becomes comparable to the strength of the coupling between \(\textbf{L}\) and \(\textbf{S}\). At that stage, the coupling between \(\textbf{L}\) and \(\textbf{S}\) breaks down, and \(J\) ceases to be a "good quantum number". \(\textbf{L}\) and \(\textbf{S}\) become separately coupled to, and precess separately around, \(\textbf{B}\). The components of \(\textbf{L}\) and \(\textbf{S}\) in the direction of \(\textbf{B}\), in units of \(\hbar\), are \(M_L\) and \(M_S\), with possible values from \(−L\) to \(+L\) and \(−S\) to \(+S\). respectively. The interaction energies between \(\textbf{L}\) and \(\textbf{B}\) and between \(\textbf{S}\) and \(\textbf{B}\), are, respectively, \(\mu_B M_L B\) and \(2\mu_B M_S B\), and there will also be a relatively small remanent spin-orbit interaction between \(L\) and \(S\), represented by \(AM_L M_S\), so the total interaction energy, which determines the splitting of the level into separate states, is \((M_L + 2M_S) \mu_B B + AM_L M_S\). This gives rise to a quite different pattern of splitting of the levels into their constituent states, and consequently a quite different pattern of the splitting of a line into its components. This is the Paschen-Back effect. The Landé splitting factor can then no longer be defined as the ratio of the magnetic moment in Bohr magnetons to the angular momentum in units of \(\hbar\). \(L\) and \(S\) are no longer coupled to each other, and \(J\) is no longer a good quantum number. Rather, the \(g\)-factor is the ratio of the sum of the components of the orbital and spin magnetic moments in the direction of \(\textbf{B}\) to the sum of the components of the orbital and spin angular momenta in that direction. That is

\[g=\frac{M_L + 2M_S}{M_L + M_S}. \label{7.22.1} \tag{7.22.1}\]

Exercise \(\PageIndex{1}\)

The first excited term of \(\text{Mg}_{\text{ I}}\) is a \(^3 \text{P}_\text{o}\) term. The separation in term values between the levels \(J = 0\) and \(J = 1\) is \(20 \ \text{cm}^{-1}\) and between \(J = 1\) and \(J = 2\) is \(40 \ \text{cm}^{-1}\), so that the multiplet evidently conforms to Landé's interval rule and hence to \(LS\)-coupling. How large a magnetic field, in tesla, would be necessary so that splitting of the states within the \(^3 \text{P}_1^\text{o}\) level is \(20 \ \text{cm}^{-1}\)?

(I make it about 29 T, which is a very strong field.)

Problem. On a sheet of graph paper, draw the three levels of a \(^3 \text{P}\) multiplet. Choose a scale so that the spin-orbit coupling coefficient (equation 7.17.1) \(a\) = one inch, so that the energy levels of the three levels of the term are at \(−2\), \(−1\) and \(+1\) inches. The \(J = 0\) level has only one state, and the \(g\)-values for the other two levels are each \(1.5\). Now apply a weak magnetic field, thus separating the states, and to the right of your zero-field energy level diagram of the three levels draw the energy levels for the nine states, such that the separation between adjacent states is one tenth of an inch. The \(J = 0\) level, of course, is not split. The other two levels are split into three and five states. Mark the value of \(M_J\) against each state. (We have previously used the symbol \(M\), but in the present context, let's call it \(M_J\) so as to be able to distinguish it from \(M_L\) and \(M_S\).) You now have the Zeeman effect. Now apply a strong field. Since \(S\) and \(L\) are each \(1\), the projections of each can be \(−1, \ 0, \ +1\), so there are nine combinations of \(M_L\) and \(M_S\). For each of these, calculate \((M_L + 2M_S) \mu_B B + AM_L M_S\) supposing that (on the scale of your graph) \(\mu_B B = 4\) inches and \(A = 0.2\) inches. Here, I'll do it:

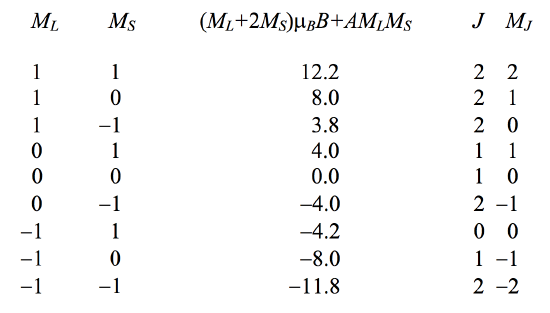
These are the energies of the states in the Paschen-Back effect, so you can now draw them on your graph paper. Leave a gap of a couple of inches between the Zeeman energies and the Paschen-Back energies. You may be interested to know how the Zeeman states correlate with the Paschen-Back states. Well, a given value of \(M_J\) correlates with the same value of \(M_S + M_L\), and that gives you two of the correlations without ambiguity. For the rest, I have tabulated, in the last column above, the \(J\) and \(M_J\) values of the Zeeman state that correlates with each Paschen-Back state. You can now join each Zeeman state to its corresponding Paschen-Back state with a straight line. You can think of the horizontal scale as being increasing magnetic field. In reality, although the Zeeman splitting starts out by increasing linearly with magnetic field, it is not linear all the way to the corresponding Paschen-Back states; the detailed calculation has to be done numerically.

Of course, in very strong magnetic fields, even the coupling between the several \(\textbf{l}\text{s}\) to form \(\textbf{L}\) and the several \(\textbf{s}\text{s}\) to form \(\textbf{S}\) breaks down, and the individual \(\textbf{l}\text{s}\) and \(\textbf{s}\text{s}\) couple strongly with \(\textbf{B}\). You then have to be careful to be sure that no two electrons have the same set of values of \(n\), \(l\), \(m_l\), \(m_s\).. This complete breakdown of the coupling of the several angular momenta to each other in favour of coupling to the magnetic field is called the complete Paschen-Back effect - but that's another story, which I don't deal with here.