22: The Boltzmann Equation

The question is: is the strength of an absorption line in a stellar spectrum related directly to the abundance of the corresponding element? The strongest lines in an A star are due to hydrogen, while the strongest lines in a G star are due to calcium; does this mean that A stars are mostly hydrogen, while G stars are mostly calcium?

In order to answer this question, we must look deep down into the structure and behavior of individual atoms. Let's focus on hydrogen, since it is the simplest of them all.

The Bohr Model of the atom

The Bohr model provides a simple, easily remembered picture of the structure of an atom:

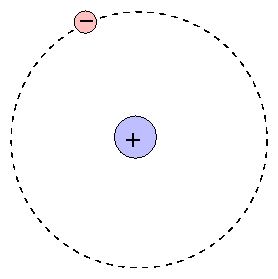
At the center is the positive nucleus, around which electron(s) move in circular orbits. The farther the electron is from the center, the higher the energy of the atom. Atoms can move from one energy state to another by absorping or emitting a photon, or by colliding with another atom or molecule. However, they are bound to jump between certain very specific energy levels:

Figure \(\PageIndex{1}\): (1) Allowed promotion, (2) allowed demotion, (3) unallowed promotion

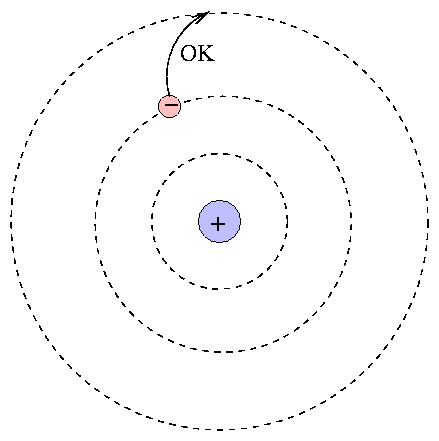
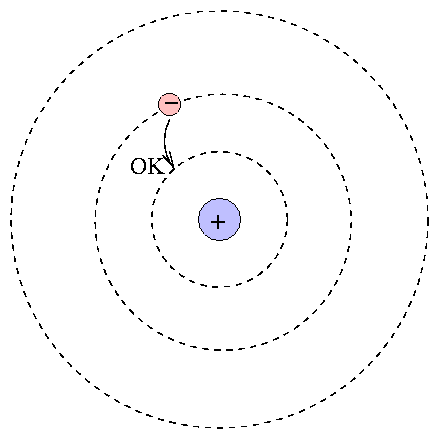
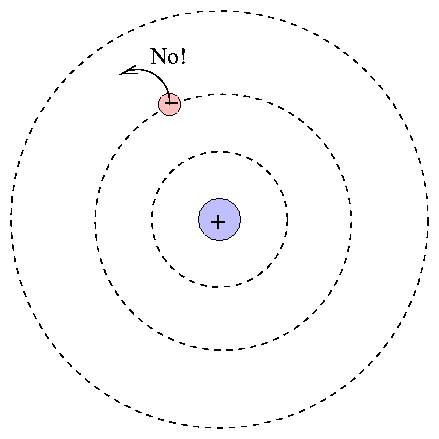
One can calculate the energy levels for hydrogen easily.

\[E_{n}=-13.6 \mathrm{eV} \frac{1}{n^{2}}\]

Exercise \(\PageIndex{1}\)

Make a table showing the energy levels for hydrogen, running from n=1 to n=3.

When an atom absorbs a photon, it jumps up to a higher level; the difference in energy of the two levels must be equal to the energy of the photon.

\[\left.E(\text { photon })=h \nu=\frac{h c}{\lambda}=E_{f}-E_{i}=(-13.6 \mathrm{eV})\right)\left(\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}}\right)\]

Exercise \(\PageIndex{2}\)

1. Make a table showing the change in energy for transitions from n=1 to n=2, n=1 to n=3, and n=2 to n=3.
2. For each transition, calculate the wavelength of a photon which must be absorbed.
3. Look at the lines in your spectra from Tuesday. Which of these lines might be produced by hydrogen?

The conditions required to create an absorption line

The Bohr model has some failures, but it will serve our purposes (and it's easy to remember, too). If we accept it, then what can we conclude from the presence of dark absorption lines in stellar spectra? Specifically, what can we conclude about the presence of H-alpha absorption lines?

Note

The lines of hydrogen in the visible part of the spectrum are given specific names because they appear so frequently. "H-alpha" refers to the n=2 to n=3 transition, "H-beta" to the n=2 to n=4 transition, "H-gamma" to the n=2 to n=5 transition, and so on.

We know that

• there must be hydrogen atoms in the solar photosphere
• there must be a source of photons deeper down in the atmosphere
• some of the hydrogen atoms must be in the n=2 state
• some of the photons must have just the right amount of energy to raise the atoms from n=2 to n=3: that's about \(\mathbf{E = 1.89 }\textbf{ eV} \mathbf{ = 3.03 \times 10^{-19}} \textbf{ J}\), corresponding to a wavelength of \(\textbf{lambda } \mathbf{ = 6563}\textbf{ Angstroms}\).

Abundances from line strengths: not so easy after all

Now that we know what's required to create a particular absorption line, we can see that the connection between line strengths and abundances isn't so simple. Going back to the example of hydrogen and calcium absorption lines,

• the hydrogen lines are produced by H atoms jumping from n=2 to n=3
• the calcium lines are produced by Ca ions jumping from n=1 to n=2

We observe the calcium lines to be stronger in the Sun, but now we realize that there could be several explanations:

1. calcium ions might outnumber hydrogen atoms in the photosphere

   and/or

2. lots of calcium ions might be in level n=1, whereas very few hydrogen atoms might be in level n=2

   and/or

3. there might be lots of photons with just the right energy to excite calcium ions to n=2, but few photons with just the right energy to excite hydrogen atoms to n=3

Hmmm. A little knowledge is a dangerous thing. We are closer to understanding stellar spectra, yet our options seem to be multiplying.

Exercise \(\PageIndex{3}\)

One of these three explanations is pretty clearly not the right answer (or, at least, not the dominant factor). Which one can we set aside, and why?

The Boltzmann equation to the rescue

If only we knew how to compute the number of atoms in a particular energy level .... then we could work backwards from the observed line strengths to the actual abundances of different types of atoms.

Under certain conditions (see below), the Boltzmann equation tells us just what we want to know: the fraction of all the atoms of a given sort which are in level n=1, or n=2, or whichever we choose. The simplest form provides a ratio of the number of atoms in two particular levels:

\[\frac{N_{b}}{N_{a}}=\left(\frac{g_{b}}{g_{a}}\right)\left(e^{-\left(E_{b}-E_{a}\right) / k T}\right)\]

Note the two terms on the right-hand side. The first term includes factors describing the degeneracy of each energy level. In a hydrogen atom, there are g = 2 ways that an atom can exist at the n=1 energy level, and g = 8 ways that an atom can arrange itself at the n=2 energy level. Calculating degeneracies for hydrogen is easy, and you can look up the values for more complex atoms.

The second factor on the right-hand side depends on two quantities: the difference in energy between the two states, and the temperature T of the gas within which the atom sits. The Boltzmass equation assumes that

• the atoms are primarily excited by collisions with other particles
• the atoms are immersed in a gas at thermal equilibrium, so that the kinetic energies and velocities of particles is described by a Maxwell-Boltzmann distribution

Under these conditions, the typical kinetic energy of a particle is

\[K E_{\mathrm{typ}} \simeq k T\]

For ordinary stellar atmospheres, these are good assumptions, and the Boltzmann equation accurately portrays the relative number of atoms of a particular sort in different energy levels.

The problem with the Balmer lines

Armed with the Boltzmann equation, we can attack the connection between line strengths and abundance quantitatively. But we soon run into a problem: the Balmer lines don't behave properly.

Look at the strength of the Balmer lines in a sequence of stellar spectra:

The Balmer lines are strongest in stars of class A0, which have temperatures of roughly T = 10,000 Kelvin. Hotter stars -- for example, B0, with T = 25,000 Kelvin -- show much weaker Balmer lines. If our model for atomic behavior is right, this must mean

• more H atoms are in the n=2 state in A0 stars than B0 stars

  and/or

• hydrogen is much more abundant in A stars than B stars

Check the first possibility:

Exercise \(\PageIndex{4}\)

1. calculate the ratio of atoms in the n=2 to n=1 energy levels for hydrogen atoms at T = 10,000 Kelvin (A stars)
2. calculate the ratio of atoms in the n=2 to n=1 energy levels for hydrogen atoms at T = 25,000 Kelvin (B stars)
3. if all stars have roughly the same abundance of hydrogen, which class ought to have stronger Balmer absorption lines?

For more information

• J. B. Tatum's "Stellar Atmospheres" text is available on-line.