19.4: Conservation of Angular Momentum about a Point
- Page ID
- 24546
So far we have introduced two conservation principles, showing that energy is constant for closed systems (no change in energy in the surroundings) and linear momentum is constant isolated system. The change in mechanical energy of a closed system is
\[W_{n c}=\Delta E_{m}=\Delta K+\Delta U, \quad(\text { closed system }) \nonumber \]
If the non-conservative work done in the system is zero, then the mechanical energy is constant,
\[0=W_{\mathrm{nc}}=\Delta E_{\mathrm{mechanical}}=\Delta K+\Delta U, \quad(\text { closed system }) \nonumber \]
The conservation of linear momentum arises from Newton’s Second Law applied to systems,
\[\overrightarrow{\mathbf{F}}^{\mathrm{ext}}=\sum_{i=1}^{N} \frac{d}{d t} \overrightarrow{\mathbf{p}}_{i}=\frac{d}{d t} \overrightarrow{\mathbf{p}}_{\mathrm{sys}} \nonumber \]
Thus if the external force in any direction is zero, then the component of the momentum of the system in that direction is a constant. For example, if there are no external forces in the x - and y -directions then
\[\begin{array}{l}
\overrightarrow{\mathbf{0}}=\left(\overrightarrow{\mathbf{F}}^{\mathrm{ext}}\right)_{x}=\frac{d}{d t}\left(\overrightarrow{\mathbf{p}}_{\mathrm{sys}}\right)_{x} \\
\overrightarrow{\mathbf{0}}=\left(\overrightarrow{\mathbf{F}}^{\mathrm{ext}}\right)_{y}=\frac{d}{d t}\left(\overrightarrow{\mathbf{p}}_{\mathrm{sys}}\right)_{y}
\end{array} \nonumber \]
We can now use our relation between torque about a point \(S\) and the change of the angular momentum about \(S\), Equation (19.3.9), to introduce a new conservation law. Suppose we can find a point \(S\) such that torque about the point \(S\) is zero,
\[\overrightarrow{\mathbf{0}}=\vec{\tau}_{S}=\frac{d \overrightarrow{\mathbf{L}}_{S}}{d t} \nonumber \]
then the angular momentum about the point \(S\) is a constant vector, and so the change in angular momentum is zero,
\[\Delta \overrightarrow{\mathbf{L}}_{s} \equiv \overrightarrow{\mathbf{L}}_{S, f}-\overrightarrow{\mathbf{L}}_{S, i}=\overrightarrow{\mathbf{0}} \nonumber \]
Thus when the torque about a point \(S\) is zero, the final angular momentum about \(S\) is equal to the initial angular momentum,
\[\overrightarrow{\mathbf{L}}_{S, f}=\overrightarrow{\mathbf{L}}_{S, i} \nonumber \]
Example \(\PageIndex{1}\): Meteor Flyby of Earth
A meteor of mass m is approaching Earth as shown in the figure. The radius of Earth is \(R_{E}\). The mass of Earth is \(M_{E}\). Assume that the meteor started very far away from Earth with speed \(v_{i}\) and at a perpendicular distance h from the axis of symmetry of the orbit. At some later time the meteor just grazes Earth (Figure 19.9). You may ignore all other gravitational forces except due to Earth. Find the distance h . Hint: What quantities are constant for this orbit?
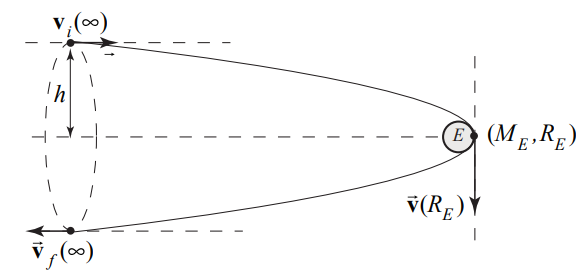
Solution
In this problem both energy and angular momentum about the center of Earth are constant (see below for justification).
The meteor’s mass is so much small than the mass of Earth that we will assume that the earth’s motion is not affected by the meteor. We’ll also need to neglect any air resistance when the meteor approaches Earth. Choose the center of Earth, (point \(S\) ) to calculate the torque and angular momentum. The force on the meteor is
\[\overrightarrow{\mathbf{F}}_{E, m}^{G}=-\frac{G m M_{E}}{r^{2}} \hat{\mathbf{r}} \nonumber \]
The vector from the center of Earth to the meteor is \(\overrightarrow{\mathbf{r}}_{S}=r \hat{r}\). The torque about \(S\) is zero because they two vectors are anti-parallel
\[\vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S} \times \overrightarrow{\mathbf{F}}_{E, m}^{G}=r \hat{\mathbf{r}} \times-\frac{G m M_{E}}{r^{2}} \hat{\mathbf{r}}=\overrightarrow{\mathbf{0}} \nonumber \]
Therefore the angular momentum about the center of Earth is a constant.
The initial angular momentum is
\[\overrightarrow{\mathbf{L}}_{S, i}=\overrightarrow{\mathbf{r}}_{S, i} \times m \overrightarrow{\mathbf{v}}_{i}=\left(x_{i} \hat{\mathbf{i}}+h \hat{\mathbf{j}}\right) \times m v \hat{\mathbf{i}}=-h m v \hat{\mathbf{k}} \nonumber \]
When the meteor just grazes Earth, the angular momentum is
\[\overrightarrow{\mathbf{L}}_{S, E}=\overrightarrow{\mathbf{r}}_{S, E} \times m \overrightarrow{\mathbf{v}}_{p}=R_{E} \hat{\mathbf{i}} \times m v_{p}(-\hat{\mathbf{j}})=-R_{E} m v_{p} \hat{\mathbf{k}} \nonumber \]
where we have used \(v_{p}\) for the speed of the meteor at its nearest approach to Earth. The constancy of angular momentum requires that
\[m v_{i} h=m v_{p} R_{E} \nonumber \]
In order to solve for h , we need to find \(v_{p}\). Because we are neglecting all forces on the meteor other than Earth’s gravity, mechanical energy is constant, and
\[\frac{1}{2} m v_{i}^{2}=\frac{1}{2} m v_{p}^{2}-\frac{G m M_{E}}{R_{E}} \nonumber \]
where we have taken the meteor to have speed \(v_{i}\) at a distance “very far away from Earth” to mean that we neglect any gravitational potential energy in the meteor-Earth system, when \(r \rightarrow \infty, U(r)=-G m M_{E} / r \rightarrow 0\). From the angular momentum condition, \(v_{p}=v_{i} h / R_{E}\) and therefore the energy condition can be rewritten as
\[v_{i}^{2}=v_{i}^{2}\left(\frac{h}{R_{E}}\right)^{2}-\frac{2 G M_{E}}{R_{E}} \nonumber \]
which we solve for the impact parameter h
\[h=\sqrt{R_{E}^{2}+\frac{2 G M_{E} R_{E}}{v_{i}^{2}}} \nonumber \]