19.2: Angular Momentum about a Point for a Particle

Angular Momentum for a Point Particle

Consider a point-like particle of mass m moving with a velocity \(\overrightarrow{\mathbf{V}}\) (Figure 19.1) with momentum \( \overrightarrow{\mathbf{p}}=m \overrightarrow{\mathbf{v}}\).

Figure \(\PageIndex{1}\): A point-like particle and its angular momentum about S.Consider a point \(S\) located anywhere in space. Let \(\overrightarrow{\mathbf{r}}_{S}\) denote the vector from the point \(S\) to the location of the object.

Define the angular momentum \(\overrightarrow{\mathbf{L}}_{s}\) about the point \(S\) of a point-like particle as the vector product of the vector from the point \(S\) to the location of the object with the momentum of the particle,

\[\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{r}}_{S} \times \overrightarrow{\mathbf{p}} \nonumber \]

The derived SI units for angular momentum are \(\left[\mathrm{kg} \cdot \mathrm{m}^{2} \cdot \mathrm{s}^{-1}\right]=[\mathrm{N} \cdot \mathrm{m} \cdot \mathrm{s}]=[\mathrm{J} \cdot \mathrm{s}]\). There is no special name for this set of units.

Because angular momentum is defined as a vector, we begin by studying its magnitude and direction. The magnitude of the angular momentum about \(S\) is given by

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=\left|\overrightarrow{\mathbf{r}}_{S}\right||\overrightarrow{\mathbf{p}}| \sin \theta \nonumber \]

where \(θ\) is the angle between the vectors and \(\overrightarrow{\mathrm{p}}\), and lies within the range \([0 \leq \theta \leq \pi]\) Analogous to the magnitude of torque, there are two ways to determine the magnitude of the angular momentum about S.

Figure \(\PageIndex{2}\): (a) Moment arm. (b) Perpendicular component of momentum.

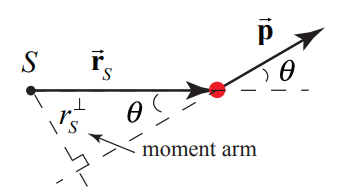
Define the moment arm, \(r_{S}^{\perp}\), (Figure \(\PageIndex{1a}\)), as the perpendicular distance from the point \(S\) to the line defined by the direction of the momentum. Then

\[r_{S}^{\perp}=\left|\overrightarrow{\mathbf{r}}_{S}\right| \sin \theta \nonumber \]

Hence the magnitude of the angular momentum is the product of the moment arm with the magnitude of the momentum,

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=r_{s}^{\perp}|\overrightarrow{\mathbf{p}}| \nonumber \]

Alternatively, let \(|\overrightarrow{\mathbf{p}}|\) denote the magnitude of the component of the momentum perpendicular to the line defined by the direction of the vector \(\overrightarrow{\mathbf{r}}_{S}\). From the geometry shown in Figure \(\PageIndex{1b}\),

\[p_{S}^{\perp}=|\overrightarrow{\mathbf{p}}| \sin \theta \nonumber \]

Thus the magnitude of the angular momentum is the product of the distance from \(S\) to the particle with \(p_{S}^{\perp}\),

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=\left|\overrightarrow{\mathbf{r}}_{s}\right| p_{s}^{\perp} \nonumber \]

Right-Hand-Rule for the Direction of the Angular Momentum

We shall define the direction of the angular momentum about the point \(S\) by a right hand rule. Draw the vectors \(\overrightarrow{\mathbf{r}}_{S} \text { and } \overrightarrow{\mathbf{p}}\) so their tails are touching. Then draw an arc starting from the vector \(\overrightarrow{\mathbf{r}}_{S}\) and finishing on the vector \(\overrightarrow{\mathrm{p}}\). (There are two such arcs; choose the shorter one.) This arc is either in the clockwise or counterclockwise direction. Curl the fingers of your right hand in the same direction as the arc. Your right thumb points in the direction of the angular momentum.

Figure 19.3 The right hand rule for determining the direction of angular momentum about \(S\).

Remember that, as in all vector products, the direction of the angular momentum about \(S\) is perpendicular to the plane formed by \(\overrightarrow{\mathbf{r}}_{S} \text { and } \overrightarrow{\mathbf{p}}\).

Example \(\PageIndex{1}\): Angular Momentum: Constant Velocity

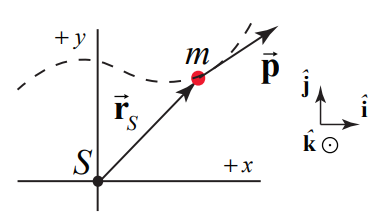
A particle of mass \(m=2.0 \mathrm{kg}\) moves as shown in Figure 19.4 with a uniform velocity \(\overrightarrow{\mathbf{v}}=3.0 \mathrm{m} \cdot \mathrm{s}^{-1} \hat{\mathbf{i}}+3.0 \mathrm{m} \cdot \mathrm{s}^{-1} \hat{\mathbf{j}}\). At time t , the particle passes through the point (2.0 m, 3.0 m). Find the direction and the magnitude of the angular momentum about the point \(S\) (the origin) at time t.

Figure 19.4 Example 19.4

Solution

Choose Cartesian coordinates with unit vectors shown in the figure above. The vector from the point \(S\) to the location of the particle is \(\overrightarrow{\mathbf{r}}_{S}=2.0 \mathrm{m} \hat{\mathbf{i}}+3.0 \mathrm{m} \hat{\mathbf{j}}\). The angular momentum vector \(\overrightarrow{\mathbf{L}}_{O}\) of the particle about the origin \(S\) is given by:

\[\begin{aligned}
\overrightarrow{\mathbf{L}}_{S} &=\overrightarrow{\mathbf{r}}_{S} \times \overrightarrow{\mathbf{p}}=\overrightarrow{\mathbf{r}}_{S} \times m \overrightarrow{\mathbf{v}} \\
&=(2.0 \mathrm{m} \hat{\mathbf{i}}+3.0 \mathrm{m} \hat{\mathbf{j}}) \times(2 \mathrm{kg})\left(3.0 \mathrm{m} \cdot \mathrm{s}^{-1} \hat{\mathbf{i}}+3.0 \mathrm{m} \cdot \mathrm{s}^{-1} \hat{\mathbf{j}}\right) \\
&=0+12 \mathrm{kg} \cdot \mathrm{m}^{2} \cdot \mathrm{s}^{-1} \hat{\mathbf{k}}-18 \mathrm{kg} \cdot \mathrm{m}^{2} \cdot \mathrm{s}^{-1}(-\hat{\mathbf{k}})+\overrightarrow{\mathbf{0}} \\
&=-6 \mathrm{kg} \cdot \mathrm{m}^{2} \cdot \mathrm{s}^{-1} \hat{\mathbf{k}}
\end{aligned} \nonumber \]

In the above, the relations \(\overrightarrow{\mathbf{i}} \times \overrightarrow{\mathbf{j}}=\overrightarrow{\mathbf{k}}, \overrightarrow{\mathbf{j}} \times \overrightarrow{\mathbf{i}}=-\overrightarrow{\mathbf{k}}, \quad \overrightarrow{\mathbf{i}} \times \overrightarrow{\mathbf{i}}=\overrightarrow{\mathbf{j}} \times \overrightarrow{\mathbf{j}}=\overrightarrow{\mathbf{0}}\) were used.

Example \(\PageIndex{2}\): Angular Momentum and Circular Motion

A particle of mass m moves in a circle of radius R about the z -axis in the x-y plane defined by z = 0 with angular velocity \(\vec{\omega}=\omega_{z} \hat{\mathbf{k}}, \omega_{z}>0\), (Figure 19.5). Find the magnitude and the direction of the angular momentum \(\overrightarrow{\mathbf{L}}_{s}\) relative to the point \(S\) lying at the center of the circular orbit, (the origin).

Figure 19.5 Example 19.2

Solution

The velocity of the particle is given by \(\overrightarrow{\mathbf{v}}=R \omega_{z} \hat{\boldsymbol{\theta}}\). The vector from the center of the circle (the point \(S\) ) to the object is given by \(\overrightarrow{\mathbf{r}}_{S}=R \hat{\mathbf{r}}\). The angular momentum about the center of the circle is the vector product

\[\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{r}}_{s} \times \overrightarrow{\mathbf{p}}=\overrightarrow{\mathbf{r}}_{S} \times m \overrightarrow{\mathbf{v}}=R m v \hat{\mathbf{k}}=R m R \omega_{z} \hat{\mathbf{k}}=m R^{2} \omega_{z} \hat{\mathbf{k}}=I_{S} \vec{\omega} \nonumber \]

The magnitude is \(\left|\overrightarrow{\mathbf{L}}_{S}\right|=m R^{2} \omega_{z}\), and the direction is in the \(+\hat{\mathbf{k}}\)-direction. For the particle, the moment of inertia about the z -axis is \(I_{S}=m R^{2}\), therefore the angular momentum about \(S\) is

\[\overrightarrow{\mathbf{L}}_{S}=I_{S} \vec{\omega} \nonumber \]

The fact that \(\overrightarrow{\mathbf{L}}_{s}\) is in the same direction as the angular velocity is due to the fact that the point \(S\) lies on the plane of motion.

Example \(\PageIndex{3}\): Angular Momentum About a Point along Central Axis for Circular Motion

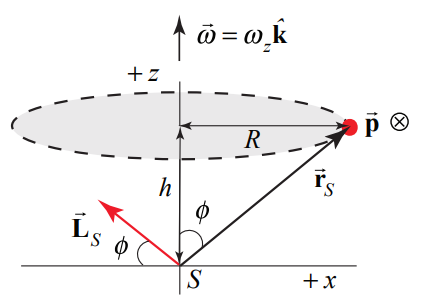
A particle of mass m moves in a circle of radius R with angular velocity \(\vec{\omega}=\omega_{z} \hat{\mathbf{k}}, \omega_{z}>0\) about the z - axis in a plane parallel to but a distance h above the x-y plane (Figure 19.6). Find the magnitude and the direction of the angular momentum \(\overrightarrow{\mathbf{L}}_{s}\) relative to the point \(S\) (the origin).

Figure 19.6 Example 19.3

Solution

The easiest way to calculate \(\overrightarrow{\mathbf{L}}_{s}\) is to use cylindrical coordinates. We begin by writing the two vectors \(\overrightarrow{\mathbf{r}}_{S} \text { and } \overrightarrow{\mathbf{p}}\) in polar coordinates. We start with the vector from point \(S\) (the origin) to the location of the moving object, \(\overrightarrow{\mathbf{r}}_{S}=R \hat{\mathbf{r}}+h \hat{\mathbf{k}}\). The momentum vector is tangent to the circular orbit so \(\overrightarrow{\mathbf{p}}=m \overrightarrow{\mathbf{v}}=m R \omega_{z} \hat{\mathbf{\theta}}\). Using the fact that \(\hat{\mathbf{r}} \times \hat{\boldsymbol{\theta}}=\hat{\mathbf{k}} \text { and } \hat{\mathbf{k}} \times \hat{\boldsymbol{\theta}}=-\hat{\mathbf{r}}\), the angular momentum about point \(S\) is

\[\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{r}}_{S} \times \overrightarrow{\mathbf{p}}=(R \hat{\mathbf{r}}+h \hat{\mathbf{k}}) \times m R \omega_{z} \hat{\mathbf{\theta}}=m R^{2} \omega_{z} \hat{\mathbf{k}}-h m R \omega_{z} \hat{\mathbf{r}} \nonumber \]

Figure 19.7 Angular momentum about the point S

The magnitude of \(\overrightarrow{\mathbf{L}}_{s}\) is given by

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=\left(\left(m R^{2} \omega_{z}\right)^{2}+\left(h m R \omega_{z}\right)^{2}\right)^{1 / 2}=m R \omega_{z}\left(h^{2}+R^{2}\right)^{1 / 2} \nonumber \]

The direction of \(\overrightarrow{\mathbf{L}}_{S}\) is given by (Figure 19.7)

\[-\frac{L_{S, z}}{L_{S, r}}=\frac{R}{h}=\tan \phi \nonumber \]

We also present a geometric argument. Suppose the particle has coordinates (x, y,h). The angular momentum about the origin is given by \(\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{r}}_{S} \times \overrightarrow{\mathbf{p}}\). The vectors \(\overrightarrow{\mathbf{r}}_{S} \text { and } \overrightarrow{\mathbf{p}}\) are perpendicular to each other so the angular momentum is perpendicular to the plane formed by those two vectors. Recall that the speed \(v=R \omega_{z}\). Suppose the vector \(\overrightarrow{\mathbf{r}}_{S}\) forms an angle \(\phi\) with the z -axis. Then \(\overrightarrow{\mathbf{L}}_{s}\) forms an angle \(\phi\) with respect to the x − y plane as shown in the figure above. The magnitude of \(\overrightarrow{\mathbf{L}}_{S}\) is

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=\left|\overrightarrow{\mathbf{r}}_{s}\right| m|\overrightarrow{\mathbf{v}}|=\left(h^{2}+R^{2}\right)^{1 / 2} m R \omega_{z} \nonumber \]

The magnitude of \(\overrightarrow{\mathbf{L}}_{s}\) is constant, but its direction is changing as the particle moves in a circular orbit about the z -axis, sweeping out a cone as shown in Figure 19.8. We draw the vector \(\overrightarrow{\mathbf{L}}_{S}\) at the origin because it is defined at that point.

Figure 19.8 Direction of angular momentum about the point \(S\) sweeps out a cone

The important point to keep in mind regarding this calculation is that for any point along the z -axis not at the center of the circular orbit of a single particle, the angular momentum about that point does not point along the z -axis but it is has a non-zero component in the x − y plane (or in the \(-\hat{\mathbf{r}}\) direction if you use polar coordinates). The z -component of the angular momentum about any point along the z -axis is independent of the location of that point along the axis.