19.6: Angular Momentum of a System of Particles

We now calculate the angular momentum about the point $S$ associated with a system of N point particles. Label each individual particle by the index $j, j=1,2, \cdots, N$. Let the $j^{\mathrm{th}}$ particle have mass $m_{j}$ and velocity $\overrightarrow{\mathbf{V}}$. The momentum of an individual particle is then $\overrightarrow{\mathbf{p}}_{j}=m_{j} \overrightarrow{\mathbf{v}}_{j}$. Let $\overrightarrow{\mathbf{r}}_{S, j}$ be the vector from the point $S$ to the $j^{\mathrm{th}}$ particle, and let $\theta_{j}$ be the angle between the vectors $\overrightarrow{\mathbf{r}}_{S, j}$ and $\overrightarrow{\mathbf{p}}_{j}$ (Figure 19.10).

Figure $\PageIndex{1}$: System of particles

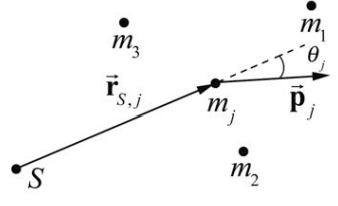
The angular momentum $\overrightarrow{\mathbf{L}}_{S, j}$ of the $j^{\text {th }}$ particle is

$$\overrightarrow{\mathbf{L}}_{S, j}=\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{p}}_{j} \nonumber$$

The angular momentum for the system of particles is the vector sum of the individual angular momenta,

$$\overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}=\sum_{j=1}^{i=N} \overrightarrow{\mathbf{L}}_{S, j}=\sum_{j=1}^{i=N} \overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{p}}_{j} \nonumber$$

The change in the angular momentum of the system of particles about a point $S$ is given by

$$\frac{d \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}}{d t}=\frac{d}{d t} \sum_{j=1}^{j=N} \overrightarrow{\mathbf{L}}_{S, j}=\sum_{j=1}^{j=N}\left(\frac{d \overrightarrow{\mathbf{r}}_{S, j}}{d t} \times \overrightarrow{\mathbf{p}}_{j}+\overrightarrow{\mathbf{r}}_{S, j} \times \frac{d \overrightarrow{\mathbf{p}}_{j}}{d t}\right) \nonumber$$

Because the velocity of the $j^{\text {th }}$ particle is $\overrightarrow{\mathbf{v}}_{S, j}=d{\mathbf{r}}_{S, j} / d t$, the first term in the parentheses vanishes (the cross product of a vector with itself is zero because they are parallel to each other)

$$\frac{d \overrightarrow{\mathbf{r}}_{S, j}}{d t} \times \overrightarrow{\mathbf{p}}_{j}=\overrightarrow{\mathbf{v}}_{S, j} \times m_{j} \overrightarrow{\mathbf{v}}_{S, j}=0 \nonumber$$

Substitute Equation (19.5.4) and $\overrightarrow{\mathbf{F}}_{j}=d \overrightarrow{\mathbf{p}}_{j} / d t$ into Equation (19.5.3) yielding

$$\frac{d \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}}{d t}=\sum_{j=1}^{i=N}\left(\overrightarrow{\mathbf{r}}_{S, j} \times \frac{d \overrightarrow{\mathbf{p}}_{j}}{d t}\right)=\sum_{j=1}^{i=N}\left(\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{F}}_{j}\right) \nonumber$$

Because

$$\sum_{j=1}^{j=N}\left(\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{F}}_{j}\right)=\sum_{j=1}^{j=N} \vec{\tau}_{S, j}=\vec{\tau}_{S}^{\mathrm{ext}}+\vec{\tau}_{S}^{\mathrm{int}} \nonumber$$

We have already shown in Chapter 17.4 that when we assume all internal forces are directed τ along the line connecting the two interacting objects then the internal torque about the point $S$ is zero,

$$\vec{\tau}_{S}^{\mathrm{int}}=\overrightarrow{\boldsymbol{0}} \nonumber$$

Equation (19.5.6) simplifies to

$$\sum_{j=1}^{i=N}\left(\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{F}}_{j}\right)=\sum_{j=1}^{j=N} \vec{\tau}_{S, j}=\vec{\tau}_{S}^{\mathrm{ext}} \nonumber$$

Therefore Equation (19.5.5) becomes

$$\vec{\tau}_{S}^{\mathrm{ext}}=\frac{d \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}}{d t} \nonumber$$

The external torque about the point $S$ is equal to the time derivative of the angular momentum of the system about that point.

Example $\PageIndex{1}$: Angular Momentum of Two Particles undergoing Circular Motion

Two identical particles of mass m move in a circle of radius R, with angular velocity $\vec{\omega}=\omega_{z} \hat{\mathbf{k}}, \omega_{z}>0$, $\omega$ about the z -axis in a plane parallel to but a distance h above the x-y plane. The particles are located on opposite sides of the circle (Figure 19.11). Find the magnitude and the direction of the angular momentum about the point $S$ (the origin).

Figure 19.11 Example 19.5

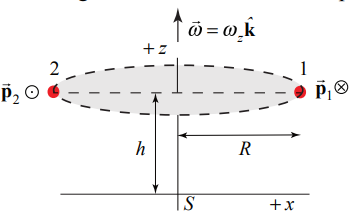
Solution

The angular momentum about the origin is the sum of the contributions from each object. The calculation of each contribution will be identical to the calculation in Example 19.3

Figure 19.12 Angular momentum of particle 1 about origin

Figure 19.13 Angular momentum of particle 2 about origin

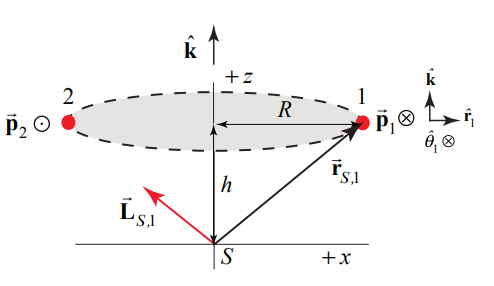
For particle 1 (Figure 19.12), the angular momentum about the point $S$ is

$$\overrightarrow{\mathbf{L}}_{S, 1}=\overrightarrow{\mathbf{r}}_{S, 1} \times \overrightarrow{\mathbf{p}}_{1}=\left(R \hat{\mathbf{r}}_{1}+h \hat{\mathbf{k}}\right) \times m R \omega_{z} \hat{\mathbf{\theta}}_{1}=m R^{2} \omega_{z} \hat{\mathbf{k}}-h m R \omega_{z} \hat{\mathbf{r}}_{1} \nonumber$$

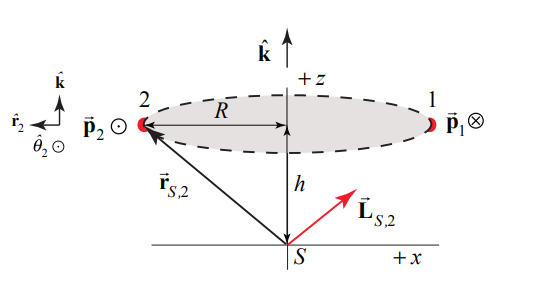
For particle 2, (Figure 19.13), the angular momentum about the point $S$ is

$$\overrightarrow{\mathbf{L}}_{S, 2}=\overrightarrow{\mathbf{r}}_{S, 2} \times \overrightarrow{\mathbf{p}}_{2}=\left(R \hat{\mathbf{r}}_{2}+h \hat{\mathbf{k}}\right) \times m R \omega_{z} \hat{\mathbf{\theta}}_{2}=m R^{2} \omega_{z} \hat{\mathbf{k}}-h m R \omega_{z} \hat{\mathbf{r}}_{2} \nonumber$$

Because the particles are located on opposite sides of the circle, $\hat{\mathbf{r}}_{1}=-\hat{\mathbf{r}}_{2}$. The vector sum only points along the z -axis and is equal to

$$\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{L}}_{S, 1}+\overrightarrow{\mathbf{L}}_{S, 2}=2 m R^{2} \omega_{z} \hat{\mathbf{k}} \nonumber$$

The two angular momentum vectors are shown in Figure 19.14.

Figure 19.14 Angular momentum about the point $S$ of both particles and their sum

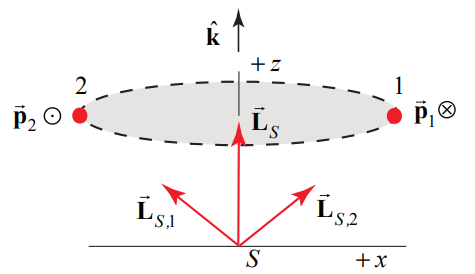
The moment of inertia of the two particles about the z -axis is given by $I_{S}=2 m R^{2}$. Therefore $\overrightarrow{\mathbf{L}}_{S}=I_{S} \vec{\omega}$. The important point about this example is that the two objects are symmetrically distributed with respect to the z -axis (opposite sides of the circular orbit). Therefore the angular momentum about any point $S$ along the z -axis has the same value $\overrightarrow{\mathbf{L}}_{s}=2 m r^{2} \omega \hat{\mathbf{k}}$ which is constant in magnitude and points in the + z -direction. This result generalizes to any rigid body in which the mass is distributed symmetrically about the axis of rotation.

Example $\PageIndex{2}$: Angular Momentum of a System of Particles about Different Points

Consider a system of N particles, and two points A and B (Figure 19.15). The angular momentum of the $j^{i h}$ particle about the point A is given by

$$\overrightarrow{\mathbf{L}}_{A, j}=\overrightarrow{\mathbf{r}}_{A, j} \times m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

Figure 19.15 Vector triangle relating position of object and points A and B

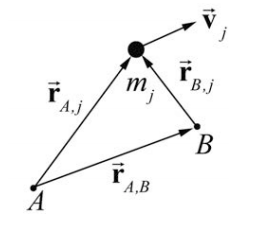
The angular momentum of the system of particles about the point A is given by the sum

$$\overrightarrow{\mathbf{L}}_{A}=\sum_{j=1}^{N} \overrightarrow{\mathbf{L}}_{A, j}=\sum_{j=1}^{N} \overrightarrow{\mathbf{r}}_{A, j} \times m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

The angular momentum about the point B can be calculated in a similar way and is given by

$$\overrightarrow{\mathbf{L}}_{B}=\sum_{j=1}^{N} \overrightarrow{\mathbf{L}}_{B, j}=\sum_{j=1}^{N} \overrightarrow{\mathbf{r}}_{B, j} \times m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

From Figure 19.15, the vectors

$$\overrightarrow{\mathbf{r}}_{A, j}=\overrightarrow{\mathbf{r}}_{B, j}+\overrightarrow{\mathbf{r}}_{A, B} \nonumber$$

We can substitute Equation (19.5.14) into Equation (19.5.12) yielding

$$\overrightarrow{\mathbf{L}}_{A}=\sum_{j=1}^{N}\left(\overrightarrow{\mathbf{r}}_{B, j}+\overrightarrow{\mathbf{r}}_{A, B}\right) \times m_{j} \overrightarrow{\mathbf{v}}_{j}=\sum_{j=1}^{N} \overrightarrow{\mathbf{r}}_{B, j} \times m_{j} \overrightarrow{\mathbf{v}}_{j}+\sum_{j=1}^{N} \overrightarrow{\mathbf{r}}_{A, B} \times m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

The first term in Equation (19.5.15) is the angular momentum about the point B . The vector $\overrightarrow{\mathbf{r}}_{A, B}$ is a constant and so can be pulled out of the sum in the second term, and Equation (19.5. 15) becomes

$$\overrightarrow{\mathbf{L}}_{A}=\overrightarrow{\mathbf{L}}_{B}+\overrightarrow{\mathbf{r}}_{A, B} \times \sum_{j=1}^{N} m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

The sum in the second term is the momentum of the system

$$\overrightarrow{\mathbf{p}}_{\mathrm{sys}}=\sum_{j=1}^{N} m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

Therefore the angular momentum about the points A and B are related by

$$\overrightarrow{\mathbf{L}}_{A}=\overrightarrow{\mathbf{L}}_{B}+\overrightarrow{\mathbf{r}}_{A, B} \times \overrightarrow{\mathbf{p}}_{\mathrm{sys}} \nonumber$$

Thus if the momentum of the system is zero, the angular momentum is the same about any point.

$$\overrightarrow{\mathbf{L}}_{A}=\overrightarrow{\mathbf{L}}_{B}, \quad\left(\overrightarrow{\mathbf{p}}_{\mathrm{sys}}=\overrightarrow{\mathbf{0}}\right) \nonumber$$

In particular, the momentum of a system of particles is zero by definition in the center of mass reference frame because in that reference frame $\overrightarrow{\mathbf{p}}_{\mathrm{sys}}=\overrightarrow{\mathbf{0}}$. Hence the angular momentum is the same about any point in the center of mass reference frame.