6.3C: Body thrown vertically upwards with initial speed v₀
( \newcommand{\kernel}{\mathrm{null}\,}\)
If we measure y upwards from the ground, the equation of motion is
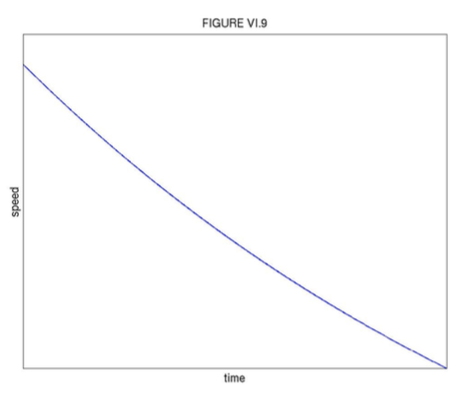
The first time integral is
and this is shown in Figure VI.9.
It reaches a maximum height after time T, when v=0(at which time the acceleration is just −g):
t+1γln(1+v0ˆv).
The second time integral (obtained by writing v as dydt in Equation 6.3.25) and the space integral (obtained by writing ¨y as vdvdy in the equation of motion) require some patience, but the results are
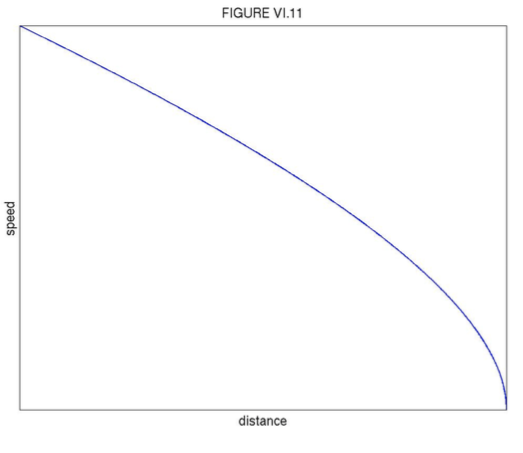
v=v0−γy−ˆvln(ˆv+v0ˆv+v).
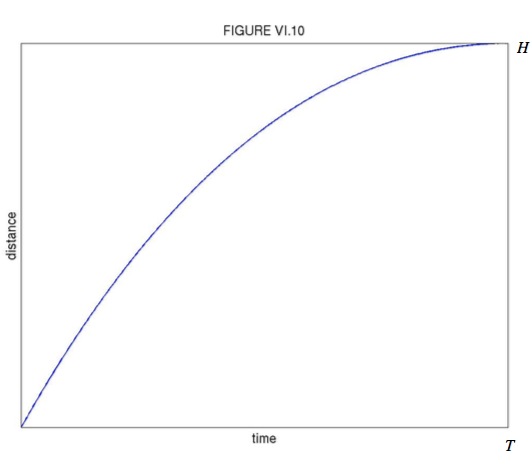
These are illustrated in Figures VI.10 and VI.11.