6.3B: Body falling under gravity in a resisting medium, resistive force proportional to the speed
( \newcommand{\kernel}{\mathrm{null}\,}\)
We are here probably considering a small sphere falling slowly through a viscous liquid, with laminar flow around the sphere, rather than a skydiver hurtling through the air. In the latter case, the airflow is likely to be highly turbulent and the resistance proportional to a higher power of the speed than the first.
We'll use the symbol y for the distance fallen. That is to say, we measure y downwards from the starting point. The equation of motion is
¨y=g−γv,
where g is the gravitational acceleration.
The body reaches a constant speed when ¨y becomes zero. This occurs at a speed ˆv=gγ, which is called the terminal speed.
To obtain the first time integral, we write the equation of motion as
dvdt=γ(ˆv−v)
or
dvˆv−v=γdt.
dvv−ˆv=−γdt.
DON'T! In the middle of an exam, while covering this derivation that you know so well, you can suddenly find yourself in inextricable difficulties. The thing to note is this. If you look at the left hand side of the equation, you will anticipate that a logarithm will appear when you integrate it. Keep the denominator positive! Some mathematicians may know the meaning of the logarithm of a negative number, but most of us ordinary mortals do not - so keep the denominator positive!
With initial condition v=0 when t=0, the first time integral becomes
v=ˆv(1−eγt).
This is illustrated in Figure VI.5.
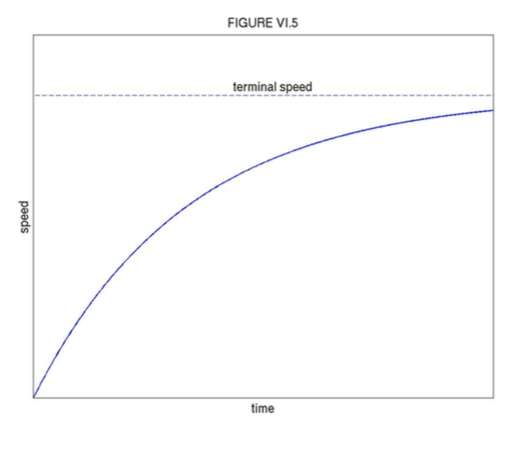
Students will have seen equations similar to this before in other branches of physics - e.g. growth of charge in a capacitor or growth of current in an inductor. That is why learning physics becomes easier all the time, because you have seen it all before in quite different contexts. Perhaps you have already noticed that third-year physics is easier than second-year physics; just think how much easier fourth-year is going to be! At any rate, v approaches the terminal speed asymptotically, never quite reaching it, but reaching half of the terminal speed in time ln2γ=.693γ (you have seen that before while studying radioactive decay), and reaching (1−e−1) = 63% of the terminal speed in time 1γ.
If the body is thrown downwards, so that its initial speed is not zero but is v=v0 when t=0, you will write the equation of motion either as Equation 6.3.10 or as Equation 6.3.11, depending on whether the initial speed is slower than or faster than the terminal speed, thus ensuring that the denominator is kept firmly positive. In either case, the result is
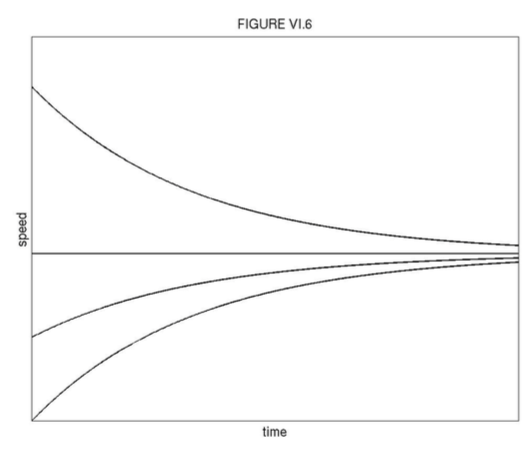
v=ˆv+(v0−ˆv)e−γt
Figure VI.6 shows v as a function of t for initial conditions v0=0,12ˆv,ˆv,2ˆv.
Returning to the initial condition v=0 when t=0, we readily find the second time integral to be
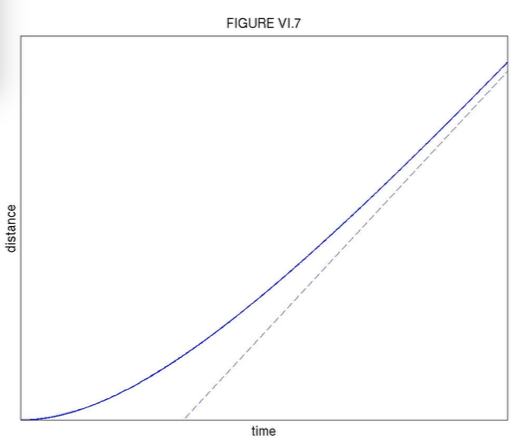
y=ˆvt−ˆvγ(1−e−γt).
You should check whether this equation is what is expected for when t=0 and when t approaches infinity. The second time integral is shown in Figure VI.7.
The space integral is found either by eliminating t between the first and second time integrals, or by writing ¨y as vdvdy in the equation of motion:
vdvdy=γ(ˆv−v),
whence
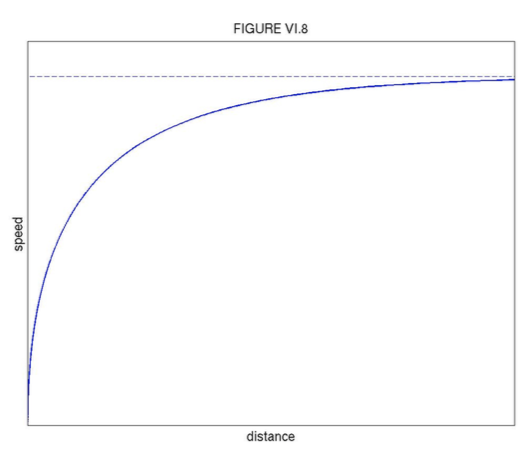
y=ˆvγln(1−vˆv)−vγ.
This is illustrated in Figure VI.8. Notice that the equation gives y as a function of v, but only
numerical calculation will give v for a given y.
Assume g = 9.8 m s-2 . A particle, starting from rest, is dropped through a medium such that the terminal speed is 9.8 m s-1. How long will it take to fall through 9.8 m?
Solution
We are asked for t, given y, and we know the equation relating t and y- it is the second time integral, Equation 6.3.14 - so what could be easier? We have γ=gˆv = 1s−1, so Equation 6.3.14 becomes
9.8=9.8t−9.8(1−e−t)
and suddenly we find that it is not as easy as expected!
The equation can be written
f(t)=t+e−t−2=0.
For Newton-Raphson iteration we need
f′(t)=1−e−t.
and, after some rearrangement, the Newton-Raphson iteration (t→t−ff′) becomes
t=1−tet−1+2.
(It may be noticed that 6.3.20, which derives from the Newton-Raphson process, is merely a rearrangement of Equation 6.3.18.)
Starting with an exceedingly stupid first guess of t = 100 s, the iterations proceed as follows:
t = 100.000 000 000
2.000 000 000
1.843 482 357
1.841 406 066
1.841 405 661
1.841 405 660 s
Assume g = 9.8 m s-2 . A particle, starting from rest, falls through a resisting medium, the damping constant being γ= 1.96 s-1 (i.e. ˆv = 5 m s-1 ). How fast is it moving after it has fallen 0.3 m?
Solution
We are asked for v, given y. We want the space integral, Equation 6.3.16. On substituting the data, we obtain
f(v)=5ln(1−0.2v)+v+0.588=0.
From this,
f′(v)=v/(v−5)
The Newton-Raphson process (t→t−ff′), after some algebra, arrives at
v=u(5ln(0.2u)+0.588)v+5=u(5lnu−7.459189560)v+5,
where u=5−v.
This time Newton-Raphson does not allow us the luxury of an exceedingly stupid first guess, but we know that the answer must lie between 0 and 5 m s-1 , so our moderately intelligent first guess can be v=2.5ms-1 .
Newton-Raphson iterations:
v = 2.500 000 000
2.122 264 100
2.051 880 531
2.049 766 247
2.049 764 400 m s-1
Problems
Here are four problems concerning a body falling from rest such that the resistance is proportional to the speed. Assume that v = 9.8 m s−2 . Answers to questions 6.3.3 - 6.3.6 are to be given to a precision of 0.0001 seconds.
A particle falls from rest in a medium such that the damping constant is γ = 1.0 s−1. How long will it take to fall through 10 m?
It takes t seconds to fall through y metres. Construct a table showing t for 201 values of y going from 0 to 20 metres in steps of 0.1 metre, assuming that γ = 1.0 s−1.
Construct a table showing t for 201 values of y going from 0 to 20 metres in steps of 0.1 metres for γ = 0.0, 0.5, 1.0, 1,5, 2.0 s . The table is to have six columns. The first column gives the distance fallen to a precision of 0.1 metres. The remaining five columns will give the time, to a precision of 0.0001 seconds, that the body takes to fall a given distance, to a precision of 0.0001 seconds
Draw, by computer, a graph showing t (the dependent variable, plotted vertically) versus y (plotted horizontally) for the five values of γ in question 3.
These four problems are in order of increasing difficulty. The first is merely an exercise in solving an implicit equation (Equation 6.3.14) numerically, and might serve as an introductory example of how, for example, to solve an equation by Newton-Raphson iteration (I make the answer 1.8656 s.) The last two, if started from scratch, could well take up an entire afternoon before it is solved to one's complete satisfaction. It might be observed that the graphs of question 4 could be drawn fairly easily by calculating y explicitly as a function of t, thus obviating the necessity of Newton-Raphson iteration. No such short cuts, however, can be made for constructing the table of question 3.
In fact I solved questions 3 and 4 in just a few minutes − but I did not start from scratch. As you progress through your scientific career, you will become aware that there are certain operations that you encounter time and time again. To do questions 3 and 4, for example, you need to be able to solve an equation by Newton-Raphson iteration; you need to be able to construct a table of a function y=f(x;a), or in this case t=f(y;γ); and you need to be able to instruct a computer to draw graphs of tabulated values. I learned long ago that all of these are problems that crop up frequently, and I therefore long ago wrote short programs (only a few lines of Fortran each) for doing each of them. All I had to do on this occasion was to marry these existing programs together, tailored to the particular functions needed. Likewise a student will recognize similar problems for which he or she frequently needs a solution. You should accumulate and keep a set of these small programs for use in the future whenever you may need them. For example, this is by no means the last time you will need Newton-Raphson iteration to solve an equation. Write a Newton-Raphson program now and keep it for future occasions!


