8.1: Force Laws

Last updated
Save as PDF

Page ID: 24466

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Those who are in love with practice without knowledge are like the sailor who gets into a ship without rudder or compass and who never can be certain whether he is going. Practice must always be founded on sound theory

~Leonardo da Vinci

There are forces that don't change appreciably from one instant to another, which we refer to as constant in time, and forces that don't change appreciably from one point to another, which we refer to as constant in space. The gravitational force on an object near the surface of the earth is an example of a force that is constant in space. There are forces that depend on the configuration of a system. When a mass is attached to one end of a spring, the spring force acting on the object increases in strength whether the spring is extended or compressed. There are forces that spread out in space such that their influence becomes less with distance. Common examples are the gravitational and electrical forces. The gravitational force between two objects falls off as the inverse square of the distance separating the objects provided the objects are of a small dimension compared to the distance between them. More complicated arrangements of attracting and repelling interactions give rise to forces that fall off with other powers of r : constant, \(1 / r, 1 / r^{2}, 1/ r^{3}\)

A force may remain constant in magnitude but change direction; for example the gravitational force acting on a planet undergoing circular motion about a star is directed towards the center of the circle. This type of attractive central force is called a centripetal force.

A force law describes the relationship between the force and some measurable property of the objects involved. We shall see that some interactions are describable by force laws and other interactions cannot be so simply described.

Hooke’s Law

In order to stretch or compress a spring from its equilibrium length, a force must be exerted on the spring. Consider an object of mass m that is lying on a horizontal surface. Attach one end of a spring to the object and fix the other end of the spring to a wall. Let \(l_{0}\) denote the equilibrium length of the spring (neither stretched or compressed). Assume that the contact surface is smooth and hence frictionless in order to consider only the effect of the spring force. If the object is pulled to stretch the spring or pushed to compress the spring, then by Newton’s Third Law the force of the spring on the object is equal and opposite to the force that the object exerts on the spring. We shall refer to the force of the spring on the object as the spring force and experimentally determine a relationship between that force and the amount of stretch or compress of the spring. Choose a coordinate system with the origin located at the point of contact of the spring and the object when the spring-object system is in the equilibrium configuration. Choose the \(\hat{\mathbf{i}}\) unit vector to point in the direction the object moves when the spring is being stretched. Choose the coordinate function x to denote the position of the object with respect to the origin (Figure 8.1).

Figure 8.1 Spring attached to a wall and an object

Initially stretch the spring until the object is at position x . Then release the object and measure the acceleration of the object the instant the object is released. The magnitude of the spring force acting on the object is \(|\overrightarrow{\mathbf{F}}|=m|\overrightarrow{\mathbf{a}}|\) Now repeat the experiment for a range of stretches (or compressions). Experiments show that for each spring, there is a range of maximum values \(x_{\max }>0\) for stretching and minimum values \(x_{\min }<0\) for compressing such that the magnitude of the measured force is proportional to the stretched or compressed length and is given by the formula.

\[|\overrightarrow{\mathbf{F}}|=k|x| \nonumber \]

where the spring constant k has units \(\mathrm{N} \cdot \mathrm{m}^{-1}\). The free-body force diagram is shown in Figure 8.2.

Figure 8.2 Spring force acting on object

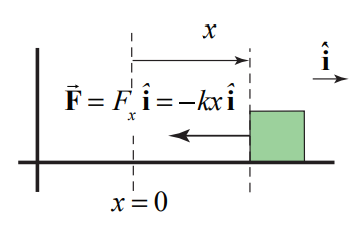
The constant k is equal to the negative of the slope of the graph of the force vs. the compression or stretch (Figure 8.3).

Figure 8.3 Plot of x -component of the spring force \(F_{x}\) vs. x

The direction of the acceleration is always towards the equilibrium position whether the spring is stretched or compressed. This type of force is called a restoring force. Let Fx denote the x -component of the spring force. Then

\[F_{x}=-k x \nonumber \]

Now perform similar experiments on other springs. For a range of stretched lengths, each spring exhibits the same proportionality between force and stretched length, although the spring constant may differ for each spring.

It would be extremely impractical to experimentally determine whether this proportionality holds for all springs, and because a modest sampling of springs has confirmed the relation, we shall infer that all ideal springs will produce a restoring force, which is linearly proportional to the stretched (or compressed) length. This experimental relation regarding force and stretched (or compressed) lengths for a finite set of springs has now been inductively generalized into the above mathematical model for ideal springs, a force law known as a Hooke’s Law.

This inductive step, referred to as Newtonian induction, is the critical step that makes physics a predictive science. Suppose a spring, attached to an object of mass m, is stretched by an amount Δx . Use the force law to predict the magnitude of the force between the rubber band and the object, \(|\overrightarrow{\mathbf{F}}|=k|\Delta x|\), without having to experimentally measure the acceleration. Now use Newton’s Second Law to predict the magnitude of the acceleration of the object.

\[|\overrightarrow{\mathrm{a}}|=\frac{|\overrightarrow{\mathbf{r}}|}{m}=\frac{k|\Delta x|}{m} \nonumber \]

Carry out the experiment, and measure the acceleration within some error bounds. If the magnitude of the predicted acceleration disagrees with the measured result, then the model for the force law needs modification. The ability to adjust, correct or even reject models based on new experimental results enables a description of forces between objects to cover larger and larger experimental domains.

Many real springs have been wound such that a force of magnitude \(F_{0}\) must be applied before the spring begins to stretch. The value of \(F_{0}\) is referred to as the pre-tension of the spring. Under these circumstances, Hooke’s law must be modified to account for this pretension,

\[\left\{\begin{array}{ll}
F_{x}=-F_{0}-k x, & x>0 \\
F_{x}=+F_{1}-k x, & x<0
\end{array}\right. \nonumber \]

Note the value of the pre-tension \(F_{0}\) and \(F_{1}\) may differ for compressing or stretching a spring.