14.4: Change in Potential Energy and Zero Point for Potential Energy

We already calculated the work done by different conservative forces: constant gravity near the surface of the earth, the spring force, and the universal gravitation force. We chose the system in each case so that the conservative force was an external force. In each case, there was no change of potential energy and the work done was equal to the change of kinetic energy,

\[W_{\mathrm{ext}}=\Delta K_{\mathrm{sys}} \nonumber \]

We now treat each of these conservative forces as internal forces and calculate the change in potential energy of the system according to our definition

\[\Delta U_{\mathrm{sys}}=-W_{\mathrm{c}}=-\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}} \cdot d \overrightarrow{\mathbf{r}} \nonumber \]

We shall also choose a zero reference potential for the potential energy of the system, so that we can consider all changes in potential energy relative to this reference potential.

Change in Gravitational Potential Energy Near Surface of the Earth

Let’s consider the example of an object falling near the surface of the earth. Choose our system to consist of the earth and the object. The gravitational force is now an internal conservative force acting inside the system. The distance separating the object and the center of mass of the earth, and the velocities of the earth and the object specifies the initial and final states.

Let’s choose a coordinate system with the origin on the surface of the earth and the + y - direction pointing away from the center of the earth. Because the displacement of the earth is negligible, we need only consider the displacement of the object in order to calculate the change in potential energy of the system.

Suppose the object starts at an initial height \(y_{i}\) above the surface of the earth and ends at final height \(y_{f}\). The gravitational force on the object is given by \(\overrightarrow{\mathbf{F}}^{g}=-m g \hat{\mathbf{j}}\), the displacement is given by \(d \overrightarrow{\mathbf{r}}=d y \hat{\mathbf{j}}\), and the scalar product is given by \(\overrightarrow{\mathbf{F}}^{g} \cdot d \overrightarrow{\mathbf{r}}=-m g \hat{\mathbf{j}} \cdot d y \hat{\mathbf{j}}=-m g d y\). The work done by the gravitational force on the object is then

\[W^{g}=\int_{y_{i}}^{y_{f}} \overrightarrow{\mathbf{F}}^{g} \cdot d \overrightarrow{\mathbf{r}}=\int_{y_{i}}^{y_{f}}-m g d y=-m g\left(y_{f}-y_{i}\right) \nonumber \]

The change in potential energy is then given by

\[\Delta U^{g}=-W^{g}=m g \Delta y=m g y_{f}-m g y_{i} \nonumber \]

We introduce a potential energy function U so that

\[\Delta U^{g} \equiv U_{f}^{g}-U_{i}^{g} \nonumber \]

Only differences in the function \(U^{g}\) have a physical meaning. We can choose a zero reference point for the potential energy anywhere we like. We have some flexibility to adapt our choice of zero for the potential energy to best fit a particular problem. Because the change in potential energy only depended on the displacement, \(\Delta y\). In the above expression for the change of potential energy (Equation (14.4.4)), let \(y_{f}=y\) be an arbitrary point and \(y_{i}=0\) denote the surface of the earth. Choose the zero reference potential for the potential energy to be at the surface of the earth corresponding to our origin \(y=0\), with \(U^{g}(0)=0\). Then

\[\Delta U^{g}=U^{g}(y)-U^{g}(0)=U^{g}(y) \nonumber \]

Substitute \(y_{i}=0, y_{f}=y\) and Equation (14.4.6) into Equation (14.4.4) yielding a potential energy as a function of the height y above the surface of the earth,

\[U^{g}(y)=m g y, \text { with } U^{g}(y=0)=0 \nonumber \]

Hooke’s Law Spring-Object System

Consider a spring-object system lying on a frictionless horizontal surface with one end of the spring fixed to a wall and the other end attached to an object of mass m (Figure 14.7). The spring force is an internal conservative force. The wall exerts an external force on the spring-object system but since the point of contact of the wall with the spring undergoes no displacement, this external force does no work.

Figure 14.7 A spring-object system.

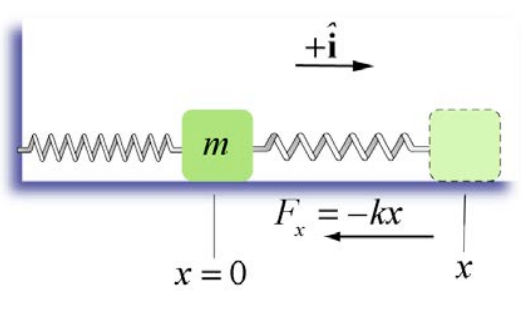
Choose the origin at the position of the center of the object when the spring is relaxed (the equilibrium position). Let x be the displacement of the object from the origin. We choose the \(+\hat{\mathbf{i}}\) unit vector to point in the direction the object moves when the spring is being stretched (to the right of x = 0 in the figure). The spring force on a mass is then given by \(\overrightarrow{\mathbf{F}}^{s}=F_{x}^{s} \hat{\mathbf{i}}=-k x \hat{\mathbf{i}}\). The displacement is \(d \overrightarrow{\mathbf{r}}=d x \hat{\mathbf{i}}\). The scalar product is \(\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=-k x \hat{\mathbf{i}} \cdot d x \hat{\mathbf{i}}=-k x d x\). The work done by the spring force on the mass is

\[W^{s}=\int_{x=x_{i}}^{x=x_{f}} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=-\frac{1}{2} \int_{x=x_{i}}^{x=x_{f}}-\frac{1}{2}(-k x) d x=-\frac{1}{2} k\left(x_{f}^{2}-x_{i}^{2}\right) \nonumber \]

We then define the change in potential energy in the spring-object system in moving the object from an initial position \(x_{i}\) from equilibrium to a final position \(x_{f}\) from equilibrium by

\[\Delta U^{\mathrm{s}} \equiv U^{\mathrm{s}}\left(x_{f}\right)-U^{\mathrm{s}}\left(x_{i}\right)=-W^{\mathrm{s}}=\frac{1}{2} k\left(x_{f}^{2}-x_{i}^{2}\right) \nonumber \]

Therefore an arbitrary stretch or compression of a spring-object system from equilibrium \(x_{i}=0\) to a final position \(x_{f}=x\) changes the potential energy by

\[\Delta U^{\mathrm{s}}=U^{\mathrm{s}}\left(x_{f}\right)-U^{\mathrm{s}}(0)=\frac{1}{2} k x^{2} \nonumber \]

For the spring-object system, there is an obvious choice of position where the potential energy is zero, the equilibrium position of the spring- object,

\[U^{\mathrm{s}}(0) \equiv 0 \nonumber \]

Then with this choice of zero reference potential, the potential energy as a function of the displacement x from the equilibrium position is given by

\[U^{s}(x)=\frac{1}{2} k x^{2}, \text { with } U^{s}(0) \equiv 0 \nonumber \]

Inverse Square Gravitation Force

Consider a system consisting of two objects of masses \(m_{1}\) and \(m_{2}\) that are separated by a center-to-center distance \(r_{2, 1}\). A coordinate system is shown in the Figure 14.8. The internal gravitational force on object 1 due to the interaction between the two objects is given by

\[\overrightarrow{\mathbf{F}}_{2,1}^{G}=-\frac{G m_{1} m_{2}}{r_{2,1}^{2}} \hat{\mathbf{r}}_{2,1} \nonumber \]

The displacement vector is given by \(d \overrightarrow{\mathbf{r}}_{2,1}=d r_{2,1} \hat{\mathbf{r}}_{2,1}\). So the scalar product is

\[\overrightarrow{\mathbf{F}}_{2,1}^{G} \cdot d \overrightarrow{\mathbf{r}}_{2,1}=-\frac{G m_{1} m_{2}}{r_{2,1}^{2}} \hat{\mathbf{r}}_{2,1} \cdot d r_{2,1} \hat{\mathbf{r}}_{2,1}=-\frac{G m_{1} m_{2}}{r_{2,1}^{2}} d r_{2,1} \nonumber \]

Figure 14.8 Gravitational interaction

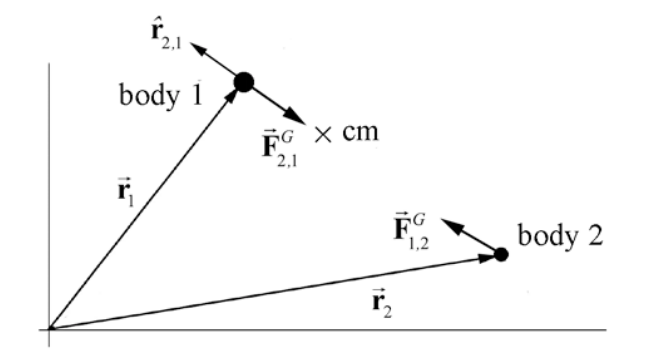
Using our definition of potential energy (Equation (14.3.4)), we have that the change in the gravitational potential energy of the system in moving the two objects from an initial position in which the center of mass of the two objects are a distance \(r_{i}\) apart to a final position in which the center of mass of the two objects are a distance \(r_{f}\) apart is given by

\[\Delta U^{G}=-\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1}^{G} \cdot d \overrightarrow{\mathbf{r}}_{2,1}=-\int_{r_{i}}^{f}-\frac{G m_{1} m_{2}}{r_{2,1}^{2}} d r_{2,1}=-\left.\frac{G m_{1} m_{2}}{r_{2,1}}\right|_{r_{i}} ^{r_{f}}=-\frac{G m_{1} m_{2}}{r_{f}}+\frac{G m_{1} m_{2}}{r_{i}} \nonumber \]

We now choose our reference point for the zero of the potential energy to be at infinity, \(r_{i}=\infty\) with the choice that \(U^{G}(\infty) \equiv 0\). By making this choice, the term \(1 / r\) in the i expression for the change in potential energy vanishes when \(r_{i}=\infty\). The gravitational potential energy as a function of the relative distance r between the two objects is given by

\[U^{G}(r)=-\frac{G m_{1} m_{2}}{r}, \text { with } U^{G}(\infty) \equiv 0 \nonumber \]