15.6: Two Dimensional Elastic Collisions

Two-dimensional Elastic Collision in Laboratory Reference Frame

Consider the elastic collision between two particles in which we neglect any external forces on the system consisting of the two particles. Particle 1 of mass \(m_{1}\) is initially moving with velocity \(\overrightarrow{\mathbf{V}}_{1, i}\) and collides elastically with a particle 2 of mass that is \(m_{2}\) initially at rest. We shall refer to the reference frame in which one particle is at rest, ‘the target’, as the laboratory reference frame. After the collision particle 1 moves with velocity \(\overrightarrow{\mathbf{V}}_{1, f}\), and particle 2 moves with velocity \(\overrightarrow{\mathbf{V}}_{2, f}\), (Figure 15.9). The angles \(\theta_{1, f}\) and \(\theta_{2, f}\) that the particles make with the positive forward direction of particle 1 are called the laboratory scattering angles.

Figure 15.9 Two-dimensional collision in laboratory reference frame

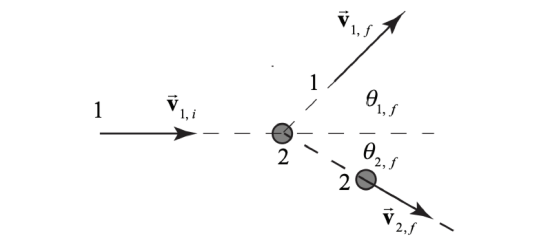
Generally the initial velocity \(\overrightarrow{\mathbf{v}}_{1, i}\) of particle 1 is known and we would like to determine the final velocities \(\overrightarrow{\mathbf{V}}_{1, f}\) and \(\overrightarrow{\mathbf{V}}_{2, f}\), which requires finding the magnitudes and directions of each of these vectors, \(v_{1, f}, v_{2, f}, \theta_{1, f}\) and \(\theta_{2, f}\) These quantities are related by the two equations describing the constancy of momentum, and the one equation describing constancy of the kinetic energy. Therefore there is one degree of freedom that we must specify in order to determine the outcome of the collision. In what follows we shall express our results for \(v_{1, f}, v_{2, f}, \text { and } \theta_{2, f}\) in terms of \(v_{1, i} \text { and } \theta_{1, f}\).

The components of the total momentum \[\overrightarrow{\mathbf{p}}_{i}^{\mathrm{sys}}=m_{1} \overrightarrow{\mathbf{v}}_{1, i}+m_{2} \overrightarrow{\mathbf{v}}_{2, i} \nonumber \] \[\begin{array}{l}
p_{x, i}^{\mathrm{sys}}=m_{1} v_{1, i} \\
p_{y, i}^{\mathrm{sys}}=0
\end{array} \nonumber \] The components of the momentum \[\overrightarrow{\mathbf{p}}_{f}^{\mathrm{sys}}=m_{1} \overrightarrow{\mathbf{v}}_{1, f}+m_{2} \overrightarrow{\mathbf{v}}_{2, f} \nonumber \] in the final state are given by \[\begin{array}{l}
p_{x, f}^{\mathrm{sys}}=m_{1} v_{1, f} \cos \theta_{1, f}+m_{2} v_{2, f} \cos \theta_{2, f} \\
p_{y, f}^{\mathrm{sys}}=m_{1} v_{1, f} \sin \theta_{1, f}-m_{2} v_{2, f} \sin \theta_{2, f}
\end{array} \nonumber \] There are no any external forces acting on the system, so each component of the total momentum remains constant during the collision, \[p_{x, i}^{\mathrm{sss}}=p_{x, f}^{\mathrm{ss}} \nonumber \] \[p_{y, i}^{\mathrm{ss}}=p_{y, f}^{\mathrm{sys}} \nonumber \] Equations (15.6.3) and (15.6.4) become \[m_{1} v_{1, i}=m_{1} v_{1, f} \cos \theta_{1, f}+m_{2} v_{2, f} \cos \theta_{2, f} \nonumber \], \[0=m_{1} v_{1, f} \sin \theta_{1, f}-m_{2} v_{2, f} \sin \theta_{2, f} \nonumber \]. The collision is elastic and therefore the system kinetic energy of is constant \[K_{i}^{\mathrm{sys}}=K_{f}^{\mathrm{sys}} \nonumber \] Using the given information, Equation (15.6.7) becomes \[\frac{1}{2} m_{1} v_{1, i}^{2}=\frac{1}{2} m_{1} v_{1, f}^{2}+\frac{1}{2} m_{2} v_{2, f}^{2} \nonumber \] Rewrite the expressions in Equations (15.6.5) and (15.6.6) as \[m_{2} v_{2, f} \cos \theta_{2, f}=m_{1}\left(v_{1, i}-v_{1, f} \cos \theta_{1, f}\right) \nonumber \] \[m_{2} v_{2, f} \sin \theta_{2, f}=m_{1} v_{1, f} \sin \theta_{1, f} \nonumber \] Square each of the expressions in Equations (15.6.9) and (15.6.10), add them together and use the identity \[\cos ^{2} \theta+\sin ^{2} \theta=1 \nonumber \] yielding \[v_{2, f}^{2}=\frac{m_{1}^{2}}{m_{2}^{2}}\left(v_{1, i}^{2}-2 v_{1, i} v_{1, f} \cos \theta_{1, f}+v_{1, f}^{2}\right) \nonumber \] Substituting Equation (15.6.11) into Equation (15.6.8) yields \[\frac{1}{2} m_{1, i}=\frac{1}{2} m_{1} v_{1, f}^{2}+\frac{1}{2} \frac{m_{1}^{2}}{m_{2}}\left(v_{1, i}^{2}-2 v_{1, i} v_{1, f} \cos \theta_{1, f}+v_{1, f}^{2}\right) \nonumber \] Equation (15.6.12) simplifies to \[0=\left(1+\frac{m_{1}}{m_{2}}\right) v_{1, f}^{2}-\frac{m_{1}}{m_{2}} 2 v_{1, i} v_{1, f} \cos \theta_{1, f}-\left(1-\frac{m_{1}}{m_{2}}\right) v_{1, i}^{2} \nonumber \] Let \(\alpha=m_{1} / m_{2}\) then Equation (15.6.13) can be written as \[0=(1+\alpha) v_{1, f}^{2}-2 \alpha v_{1, i} v_{1, f} \cos \theta_{1, f}-(1-\alpha) v_{1, i}^{2} \nonumber \] The solution to this quadratic equation is given by \[v_{1, f}=\frac{\alpha v_{1, i} \cos \theta_{1, f} \pm\left(\alpha^{2} v_{1, i}^{2} \cos ^{2} \theta_{1, f}+(1-\alpha) v_{1, i}^{2}\right)^{1 / 2}}{(1+\alpha)} \nonumber \] Divide the expressions in Equation (15.6.9), yielding \[\frac{v_{2, f} \sin \theta_{2, f}}{v_{2, f} \cos \theta_{2, f}}=\frac{v_{1, f} \sin \theta_{1, f}}{v_{1, i}-v_{1, f} \cos \theta_{1, f}} \nonumber \] Equation (15.6.16) simplifies to \[\tan \theta_{2, f}=\frac{v_{1, f} \sin \theta_{1, f}}{v_{1, i}-v_{1, f} \cos \theta_{1, f}} \nonumber \]

The relationship between the scattering angles in Equation (15.6.17) is independent of the masses of the colliding particles. Thus the scattering angle for particle 2 is \[\theta_{2, f}=\tan ^{-1}\left(\frac{v_{1, f} \sin \theta_{1, f}}{v_{1, i}-v_{1, f} \cos \theta_{1, f}}\right) \nonumber \] We can now use Equation (15.6.10) to find an expression for the final velocity of particle 1 \[v_{2, f}=\frac{v_{1, f} \sin \theta_{1, f}}{\alpha \sin \theta_{2, f}} \nonumber \]

Example 15.5 Elastic Two-dimensional collision of identical particles

Figure 15.10 Momentum flow diagram for two-dimensional elastic collision

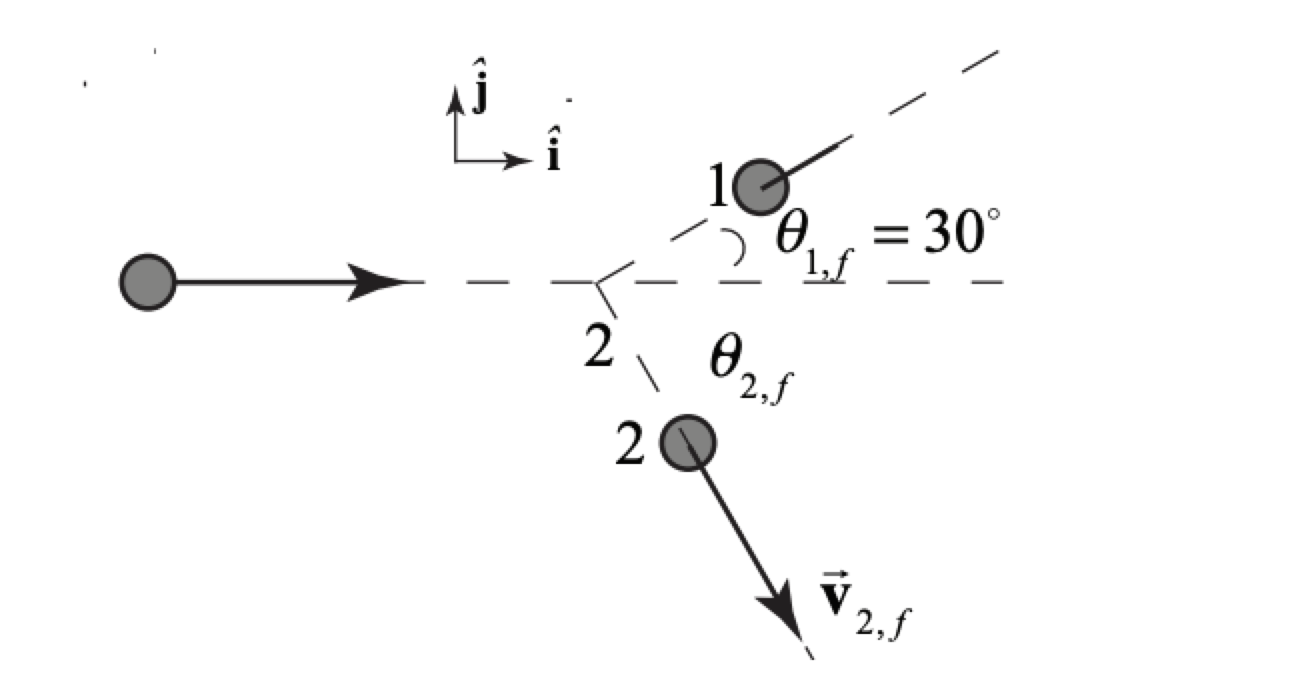
Object 1 with mass is initially moving with a speed = 3.0\(\mathrm{m} \cdot \mathrm{s}^{-1}\) and collides elastically with object 2 that has the same mass, \(m_{2}=m_{1}\), and is initially at rest. After the collision, object 1 moves with an unknown speed \(v_{1, f}\) at an angle \(\theta_{1, f}\), with respect to its initial direction of motion and object 2 moves with an unknown speed \(v_{2, f}\), at an unknown angle \(\theta_{2, f}\), f (as shown in the Figure 15.10). Find the final speeds of each of the objects and the angle \(\theta_{2, f}\).

Solution

Because the masses are equal, \(\alpha=1\). We are given that \(v_{1, i}=3.0 \mathrm{m} \cdot \mathrm{s}^{-1}\). We are given that \(v_{1, i}=3.0 \mathrm{m} \cdot \mathrm{s}^{-1}\) and \(\theta_{1, f}=30^{\circ}\). Hence Equation (15.5.14) reduces to \[v_{1, f}=v_{1, i} \cos \theta_{1, f}=\left(3.0 \mathrm{m} \cdot \mathrm{s}^{-1}\right) \cos 30^{\circ}=2.6 \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber \]

Substituting Equation (15.6.20) in Equation (15.6.17) yields \[\begin{aligned}
\theta_{2, f} &=\tan ^{-1}\left(\frac{v_{1, f} \sin \theta_{1, f}}{v_{1, i}-v_{1, f} \cos \theta_{1, f}}\right) \\
\theta_{2, f} &=\tan ^{-1}\left(\frac{\left(2.6 \mathrm{m} \cdot \mathrm{s}^{-1}\right) \sin \left(30^{\circ}\right)}{3.0 \mathrm{m} \cdot \mathrm{s}^{-1}-\left(2.6 \mathrm{m} \cdot \mathrm{s}^{-1}\right) \cos \left(30^{\circ}\right)}\right) \\
&=60^{\circ}
\end{aligned} \nonumber \] The above results for \(v_{1, f}\) and \(\theta_{2, f}\) may be substituted into either of the expressions in Equation (15.6.9), or Equation (15.6.11), to find \(v_{2, f}=1.5 \mathrm{m} \cdot \mathrm{s}^{-1}\). Equation (15.6.11) also has the solution \(v_{2, f} = 0\), which would correspond to the incident particle missing the target completely.

Before going on, the fact that \(\theta_{1, f}+\theta_{2, f}=90^{\circ}\) that is, the objects move away from the collision point at right angles, is not a coincidence. A vector derivation is presented in Example 15.6. We can see this result algebraically from the above result. Substituting Equation (15.6.20) \(v_{1, f}=v_{1, i} \cos \theta_{1, f}\) in Equation (15.6.17) yields \[\tan \theta_{2, f}=\frac{\cos \theta_{1, f} \sin \theta_{1, f}}{1-\cos \theta_{1, f}^{2}}=\cot \theta_{1, f}=\tan \left(90^{\circ}-\theta_{1, f}\right) \nonumber \] showing that \(\theta_{1, f}+\theta_{2, f}=90^{\circ}\), the angles \(\theta_{1, f}\) and \(\theta_{2, f}\) are complements.

Example 15.6 Two-dimensional elastic collision between particles of equal mass

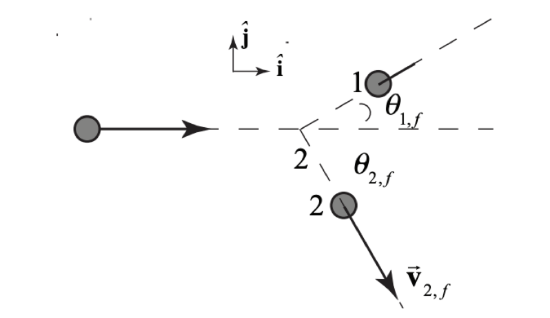
Show that the equal mass particles emerge from a two-dimensional elastic collision at right angles by making explicit use of the fact that momentum is a vector quantity.

Figure 15.11 Elastic scattering of identical particles

Solution

Choose a reference frame in which particle 2 is initially at rest (Figure 15.11). There are no external forces acting on the two objects during the collision (the collision forces are all internal), therefore momentum is constant \[\overrightarrow{\mathbf{p}}_{i}^{\mathrm{sys}}=\overrightarrow{\mathbf{p}}_{f}^{\mathrm{sys}} \nonumber \] which becomes \[m_{1} \overrightarrow{\mathbf{v}}_{1, i}=m_{1} \overrightarrow{\mathbf{v}}_{1, f}+m_{1} \overrightarrow{\mathbf{v}}_{2, f} \nonumber \] Equation (15.6.24) simplifies to \[\overrightarrow{\mathbf{v}}_{1, i}=\overrightarrow{\mathbf{v}}_{1, f}+\overrightarrow{\mathbf{v}}_{2, f} \nonumber \] Recall the vector identity that the square of the speed is given by the dot product \(\overrightarrow{\mathbf{v}} \cdot \overrightarrow{\mathbf{v}}=v^{2}\). With this identity in mind, we take the dot product of each side of Equation (15.6.25) with itself, \[\begin{aligned}
\overrightarrow{\mathbf{v}}_{1, i} \cdot \overrightarrow{\mathbf{v}}_{1, i} &=\left(\overrightarrow{\mathbf{v}}_{1, f}+\overrightarrow{\mathbf{v}}_{2, f}\right) \cdot\left(\overrightarrow{\mathbf{v}}_{1, f}+\overrightarrow{\mathbf{v}}_{2, f}\right) \\
&=\overrightarrow{\mathbf{v}}_{1, f} \cdot \overrightarrow{\mathbf{v}}_{1, f}+2 \overrightarrow{\mathbf{v}}_{1, f} \cdot \overrightarrow{\mathbf{v}}_{2, f}+\overrightarrow{\mathbf{v}}_{2, f} \cdot \overrightarrow{\mathbf{v}}_{2, f}
\end{aligned} \nonumber \] This becomes \[v_{1, i}^{2}=v_{1, f}^{2}+2 \overrightarrow{\mathbf{v}}_{1, f} \cdot \overrightarrow{\mathbf{v}}_{2, f}+v_{2, f}^{2} \nonumber \] Recall that kinetic energy is the same before and after an elastic collision, and the masses of the two objects are equal, so constancy of energy, (Equation (15.4.2)) simplifies to \[v_{1, i}^{2}=v_{1, f}^{2}+v_{2, f}^{2} \nonumber \] Comparing Equation (15.6.27) to Equation (15.6.28), we see that \[\overrightarrow{\mathbf{v}}_{1, f} \cdot \overrightarrow{\mathbf{v}}_{2, f}=0 \nonumber \] The dot product of two nonzero vectors is zero when the two vectors are at right angles to each other justifying our claim that the collision particles emerge at right angles to each other.

Example 15.7 Two-dimensional collision between particles of unequal mass

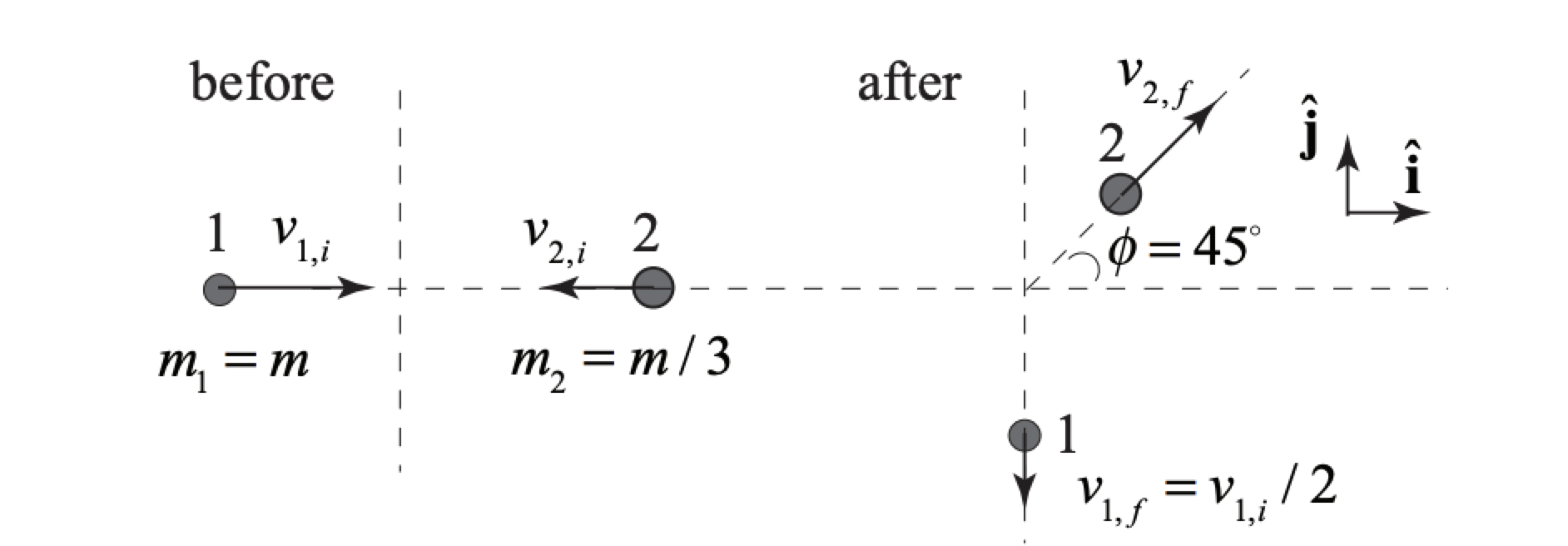
Particle 1 of mass \(m_{1}\), initially moving in the positive x-direction (to the right in the figure below) with speed \(v_{1, i}\) collides with particle 2 of mass \(m_{2}=m_{1} / 3\) which is initially moving in the opposite direction (Figure 15.12) with an unknown speed \(v_{2, i}\). Assume that the total external force acting on the particles is zero. Do not assume the collision is elastic. After the collision, particle 1 moves with speed \(v_{1, f}=v_{1, i} / 2\) in the negative y-direction. After the collision, particle 2 moves with an unknown speed \(v_{2, f}\) at an angle \(\theta_{2, f}=45^{\circ}\) with respect to the positive x-direction. (i) Determine the initial speed \(v_{2 i}\) of particle 2 and the final speed \(v_{2, f}\) of particle 2 in terms of \(\mathcal{V}_{1, i}\). (ii) Is the collision elastic?

Figure 15.12 Two-dimensional collision between particles of unequal mass

Solution

We choose as our system the two particles. We are given that \(v_{1, f}=v_{1, i} / 2\). We apply the two momentum conditions, \[m_{1} v_{1, i}-\left(m_{1} / 3\right) v_{2, i}=\left(m_{1} / 3\right) v_{2, f}(\sqrt{2} / 2) \nonumber \] \[0=m_{1} v_{1, f}-\left(m_{1} / 3\right) v_{2, f}(\sqrt{2} / 2) \nonumber \] Solve Equation (15.5.31) for \(v_{2, f}\): \[v_{2, f}=3 \sqrt{2} v_{1, f}=\frac{3 \sqrt{2}}{2} v_{1, i} \nonumber \] Substitute Equation (15.6.32) into Equation (15.6.30) and solve for \(v_{2, i}\) \[v_{2, i}=(3 / 2) v_{1, i} \nonumber \] The initial kinetic energy is then \[K_{i}=\frac{1}{2} m_{1} v_{1, i}^{2}+\frac{1}{2}\left(m_{1} / 3\right) v_{2, i}^{2}=\frac{7}{8} m_{1} v_{1, i}^{2} \nonumber \] The final kinetic energy is \[K_{f}=\frac{1}{2} m_{1} v_{1, f}^{2}+\frac{1}{2} m_{2} v_{2, f}^{2}=\frac{1}{8} m_{1} v_{1, i}^{2}+\frac{3}{4} m_{1} v_{1, i}^{2}=\frac{7}{8} m_{1} v_{1, i}^{2} \nonumber \] Comparing our results, we see that kinetic energy is constant so the collision is elastic.