16.4: Conservation of Energy for Fixed Axis Rotation

Consider a closed system \(\left(\Delta E_{\text {system}}=0\right)\) under action of only conservative internal forces. Then the change in the mechanical energy of the system is zero

\[\Delta E_{m}=\Delta U+\Delta K=\left(U_{f}+K_{f}\right)-\left(U_{i}+K_{i}\right)=0 \nonumber \]

For fixed axis rotation with a component of angular velocity ω about the fixed axis, the change in kinetic energy is given by

\[\Delta K \equiv K_{f}-K_{i}=\frac{1}{2} I_{S} \omega_{f}^{2}-\frac{1}{2} I_{S} \omega_{i}^{2} \nonumber \]

where \(S\) is a point that lies on the fixed axis. Then conservation of energy implies that

\[U_{f}+\frac{1}{2} I_{S} \omega_{f}^{2}=U_{i}+\frac{1}{2} I_{S} \omega_{i}^{2} \nonumber \]

Example 16.4 Energy and Pulley System

A wheel in the shape of a uniform disk of radius R and mass \(m_{\mathrm{p}}\) is mounted on a frictionless horizontal axis. The wheel has moment of inertia about the center of mass \(I_{\mathrm{cm}}=(1 / 2) m_{\mathrm{p}} R^{2}\) A massless cord is wrapped around the wheel and one end of the cord is attached to an object of mass \(m_{2}\) that can slide up or down a frictionless inclined plane. The other end of the cord is attached to a second object of mass \(m_{1}\) that hangs over the edge of the inclined plane. The plane is inclined from the horizontal by an angle θ (Figure 16.12). Once the objects are released from rest, the cord moves without slipping around the disk. Calculate the speed of block 2 as a function of distance that it moves down the inclined plane using energy techniques. Assume there are no energy losses due to friction and that the rope does not slip around the pulley

Figure 16.13 Coordinate system for pulley and blocks

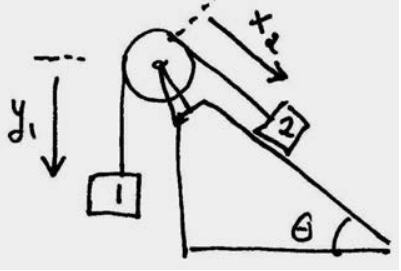
Solution: Define a coordinate system as shown in Figure 16.13. Choose the zero for the gravitational potential energy at a height equal to the center of the pulley. In Figure 16.14 illustrates the energy diagrams for the initial state and a dynamic state at an arbitrary time when the blocks are sliding.

Figure 16.14 Energy diagrams for initial state and dynamic state at arbitrary time

Then the initial mechanical energy is

\[E_{i}=U_{i}=-m_{1} g y_{1, i}-m_{2} g x_{2, i} \sin \theta \nonumber \]

The mechanical energy, when block 2 has moved a distance

\[d=x_{2}-x_{2, i} \nonumber \]

is given by

\[E=U+K=-m_{1} g y_{1}-m_{2} g x_{2} \sin \theta+\frac{1}{2} m_{1} v_{1}^{2}+\frac{1}{2} m_{2} v_{2}^{2}+\frac{1}{2} I_{p} \omega^{2} \nonumber \]

The rope connects the two blocks, and so the blocks move at the same speed

\[v \equiv v_{1}=v_{2} \nonumber \]

The rope does not slip on the pulley; therefore as the rope moves around the pulley the tangential speed of the rope is equal to the speed of the blocks

\[v_{\tan }=R \omega=v \nonumber \]

Equation (16.3.6) can now be simplified

\[E=U+K=-m_{1} g y_{1}-m_{2} g x_{2} \sin \theta+\frac{1}{2}\left(m_{1}+m_{2}+\frac{I_{P}}{R^{2}}\right) v^{2} \nonumber \]

Because we have assumed that there is no loss of mechanical energy, we can set \(E_{i}=E\) and find that

\[-m_{1} g y_{1, i}-m_{2} g x_{2, i} \sin \theta=-m_{1} g y_{1}-m_{2} g x_{2} \sin \theta+\frac{1}{2}\left(m_{1}+m_{2}+\frac{I_{P}}{R^{2}}\right) v^{2} \nonumber \]

which simplifies to

\[-m_{1} g\left(y_{1,0}-y_{1}\right)+m_{2} g\left(x_{2}-x_{2,0}\right) \sin \theta=\frac{1}{2}\left(m_{1}+m_{2}+\frac{I_{P}}{R^{2}}\right) v^{2} \nonumber \]

We finally note that the movement of block 1 and block 2 are constrained by the relationship

\[d=x_{2}-x_{2, i}=y_{1, i}-y_{1} \nonumber \]

Then Equation (16.3.11) becomes

\[g d\left(-m_{1}+m_{2} \sin \theta\right)=\frac{1}{2}\left(m_{1}+m_{2}+\frac{I_{P}}{R^{2}}\right) v^{2} \nonumber \]

We can now solve for the speed as a function of distance \(d=x_{2}-x_{2, i}\) that block 2 has traveled down the incline plane

\[v=\sqrt{\frac{2 g d\left(-m_{1}+m_{2} \sin \theta\right)}{\left(m_{1}+m_{2}+\left(I_{P} / R^{2}\right)\right)}} \nonumber \]

If we assume that the moment of inertial of the pulley is \(I_{\mathrm{cm}}=(1 / 2) m_{\mathrm{p}} R^{2}\), then the speed becomes

\[v=\sqrt{\frac{2 g d\left(-m_{1}+m_{2} \sin \theta\right)}{\left(m_{1}+m_{2}+(1 / 2) m_{P}\right)}} \nonumber \]

Example 16.5 Physical Pendulum

A physical pendulum consists of a uniform rod of mass \(m_{1}\) pivoted at one end about the point \(S\). The rod has length \(l_{1}\) and moment of inertia \(I_{1}\) about the pivot point. A disc of mass \(m_{2}\) and radius \(r_{2}\) with moment of inertia \(I_{\mathrm{cm}}\) about its center of mass is rigidly attached a distance \(l_{2}\) from the pivot point. The pendulum is initially displaced to an angle \(\theta_{i}\) and then released from rest. (a) What is the moment of inertia of the physical pendulum about the pivot point \(S\) ? (b) How far from the pivot point is the center of mass of the system? (c) What is the angular speed of the pendulum when the pendulum is at the bottom of its swing?

Figure 16.15 Rod and with fixed disc pivoted about the point S

Solution: a) The moment of inertia about the pivot point is the sum of the moment of inertia of the rod, given as \(I_{1}\), and the moment of inertia of the disc about the pivot point. The moment of inertia of the disc about the pivot point is found from the parallel axis theorem,

\[I_{\text {disc }}=I_{\mathrm{cm}}+m_{2} l_{2}^{2} \nonumber \]

The moment of inertia of the system consisting of the rod and disc about the pivot point \(S\) is then

\[I_{S}=I_{1}+I_{\mathrm{disc}}=I_{1}+I_{\mathrm{cm}}+m_{2} l_{2}^{2} \nonumber \]

The center of mass of the system is located a distance from the pivot point

\[l_{\mathrm{cm}}=\frac{m_{1}\left(l_{1} / 2\right)+m_{2} l_{2}}{m_{1}+m_{2}} \nonumber \]

b) We can use conservation of mechanical energy, to find the angular speed of the pendulum at the bottom of its swing. Take the zero point of gravitational potential energy to be the point where the bottom of the rod is at its lowest point, that is, \(\theta=0\). The initial state energy diagram for the rod is shown in Figure 16.16a and the initial state energy diagram for the disc is shown in Figure 16.16b.

Figure 16.16 (a) Initial state energy diagram for rod (b) Initial state energy diagram for disc

The initial mechanical energy is then

\[E_{i}=U_{i}=m_{1} g\left(l_{1}-\frac{l_{1}}{2} \cos \theta_{i}\right)+m_{2} g\left(l_{1}-l_{2} \cos \theta_{i}\right) \nonumber \]

At the bottom of the swing, \(\theta_{f}=0\), and the system has angular velocity ω f . The mechanical energy at the bottom of the swing is

\[E_{f}=U_{f}+K_{f}=m_{1} g \frac{l_{1}}{2}+m_{2} g\left(l_{1}-l_{2}\right)+\frac{1}{2} I_{S} \omega_{f}^{2} \nonumber \]

with \(I_{S}\) as found in Equation (16.3.17). There are no non-conservative forces acting, so the mechanical energy is constant therefore equating the expressions in (16.3.19) and (16.3.20) we get that

\[m_{1} g\left(l_{1}-\frac{l_{1}}{2} \cos \theta_{i}\right)+m_{2} g\left(l_{1}-l_{2} \cos \theta_{i}\right)=m_{1} g \frac{l_{1}}{2}+m_{2} g\left(l_{1}-l_{2}\right)+\frac{1}{2} I_{S} \omega_{f}^{2} \nonumber \]

This simplifies to

\[\left(\frac{m_{1} l_{1}}{2}+m_{2} l_{2}\right) g\left(1-\cos \theta_{i}\right)=\frac{1}{2} I_{S} \omega_{f}^{2} \nonumber \]

We now solve for \(\omega_{f}\) (taking the positive square root to insure that we are calculating angular speed)

\[\omega_{f}=\sqrt{\frac{2\left(\frac{m_{1} l_{1}}{2}+m_{2} l_{2}\right) g\left(1-\cos \theta_{i}\right)}{I_{S}}} \nonumber \]

Finally we substitute in Equation(16.3.17) in to Equation (16.3.23) and find

\[\omega_{f}=\sqrt{\frac{2\left(\frac{m_{1} l_{1}}{2}+m_{2} l_{2}\right) g\left(1-\cos \theta_{i}\right)}{I_{1}+I_{\mathrm{cm}}+m_{2} l_{2}^{2}}} \nonumber \]

Note that we can rewrite Equation (16.3.22), using Equation (16.3.18) for the distance between the center of mass and the pivot point, to get

\[\left(m_{1}+m_{2}\right) l_{c m} g\left(1-\cos \theta_{i}\right)=\frac{1}{2} I_{S} \omega_{f}^{2} \nonumber \]

We can interpret this equation as follows. Treat the system as a point particle of mass \(m_{1}+m_{2}\) located at the center of mass \(l_{c m}\). Take the zero point of gravitational potential energy to be the point where the center of mass is at its lowest point, that is, \(\theta=0\). Then

\[E_{i}=\left(m_{1}+m_{2}\right) l_{c m} g\left(1-\cos \theta_{i}\right) \nonumber \]

\[E_{f}=\frac{1}{2} I_{S} \omega_{f}^{2} \nonumber \]

Thus conservation of energy reproduces Equation (16.3.25).