19.8: Principle of Conservation of Angular Momentum

Consider a system of particles. We begin with the result that we derived in Section 19.7 that the torque about a point \(S\) is equal to the time derivative of the angular momentum about that point S,

\begin{equation}\vec{\tau}_{S}^{\mathrm{ext}}=\frac{d \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}}{d t}\end{equation}

With this assumption, the torque due to the external forces is equal to the rate of change of the angular momentum

\begin{equation}\vec{\tau}_{S}^{\mathrm{ext}}=\frac{d \overrightarrow{\mathrm{L}}_{S}^{\mathrm{sys}}}{d t}\end{equation}

Principle of Conservation of Angular Momentum

If the external torque acting on a system is zero, then the angular momentum of the system is constant. So for any change of state of the system the change in angular momentum is zero

\begin{equation}\Delta \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}} \equiv\left(\overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}\right)_{f}-\left(\overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}\right)_{i}=\overrightarrow{\mathbf{0}}\end{equation}

Equivalently the angular momentum is constant

\begin{equation}\left(\overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}\right)_{f}=\left(\overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}\right)_{i}\end{equation}

So far no isolated system has been encountered such that the angular momentum is not constant so our assumption that internal torques cancel is pairs can be taken as an experimental observation.

Example \(\PageIndex{1}\): Collision Between Pivoted Rod and Object

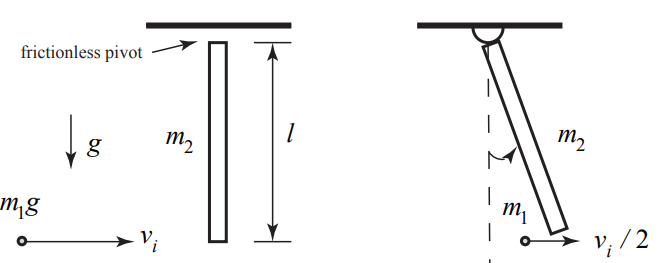
A point-like object of mass \(m_{1}\) moving with constant speed \(v_{i}\) strikes a rigid uniform rod of length l and mass \(m_{2}\) that is hanging by a frictionless pivot from the ceiling. Immediately after striking the rod, the object continues forward but its speed decreases to \(v_{i} / 2\) (Figure 19.19). The moment of inertia of the rod about its center of mass is

\[I_{c m}=(1 / 12) m_{2} l^{2} \nonumber \]

Gravity acts with acceleration g downward.

1. (a) For what value of \(v_{i}\) will the rod just touch the ceiling on its first swing?
2. (b) For what ratio \(m_{2} / m_{1}\) will the collision be elastic?

Figure 19.19 Example 19.7

Solution

We begin by identifying our system, which consists of the object and the uniform rod. We identify three states; an initial state i : immediately before the collision, state a : immediately after the collision, and state f : the instant the rod touches the ceiling when the final angular speed is zero. We would like to know if any of our fundamental quantities: momentum, energy, and angular momentum, are constant during these state changes, state i to state a , state a to state f.

Figure 19.20 Free-body force diagrams on particle and rod

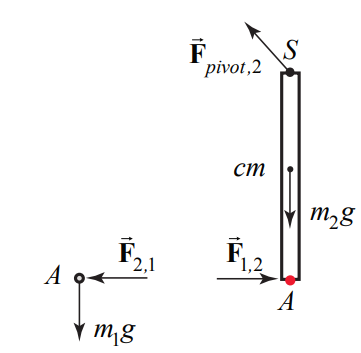
We start with the transition from state i to state a . The pivot force holding the rod to the ceiling is an external force acting at the pivot point \(S\). There is also the gravitational force acting at the center of mass of the rod and on the object. There are also internal forces due to the collision of the rod and the object at point A (Figure 19.20).

The external force means that momentum is not constant. The point of action of the external pivot force is fixed and so does no work. However, we do not know whether or not the collision is elastic and so we cannot assume that mechanical energy is constant. Choose the pivot point \(S\) as the point about which to calculate torque, then the torque diagrams are shown in Figure 19.21.

Figure 19.21 Torque diagrams on particle and rod with torque calculated about pivot point S

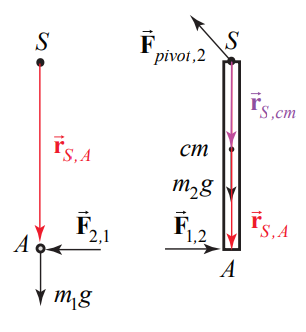
The torque on the system about the pivot \(S\) is then the sum of terms

\begin{equation}\vec{\tau}_{S}^{\mathrm{sys}}=\overrightarrow{\mathbf{r}}_{S, S} \times \overrightarrow{\mathbf{F}}_{\text {pivot}, 2}+\overrightarrow{\mathbf{r}}_{S, A} \times \overrightarrow{\mathbf{F}}_{1,2}+\overrightarrow{\mathbf{r}}_{S, A} \times \overrightarrow{\mathbf{F}}_{2,1}+\overrightarrow{\mathbf{r}}_{S, c m} \times m_{2} \overrightarrow{\mathbf{g}}+\overrightarrow{\mathbf{r}}_{S, A} \times m_{1} \overrightarrow{\mathbf{g}} \cdot(19.5 .37)\end{equation}

The external pivot force does not contribute any torque because \(\overrightarrow{\mathbf{r}}_{S, S}=\overrightarrow{\mathbf{0}}\). The internal forces between the rod and the object are equal in magnitude and opposite in direction, \(\overrightarrow{\mathbf{F}}_{1,2}=-\overrightarrow{\mathbf{F}}_{2,1}\) (Newton’s Third Law), and so their contributions to the torque add to zero. If the collision is instantaneous then the gravitational force is parallel to \(\overrightarrow{\mathbf{r}}_{S, c m} \text { and } \overrightarrow{\mathbf{r}}_{S, A}\) so the two gravitational torques are zero. Therefore the torque on the system about the pivot point is zero, \(\vec{\tau}_{S}^{\mathrm{sys}}=\overrightarrow{0}\). Thus the angular momentum about the pivot point is constant,

\begin{equation}\overrightarrow{\mathbf{L}}_{S, i}^{\mathrm{sys}}=\overrightarrow{\mathbf{L}}_{S, a}^{\mathrm{sys}}\end{equation}

Figure 19.22 Angular momentum diagram

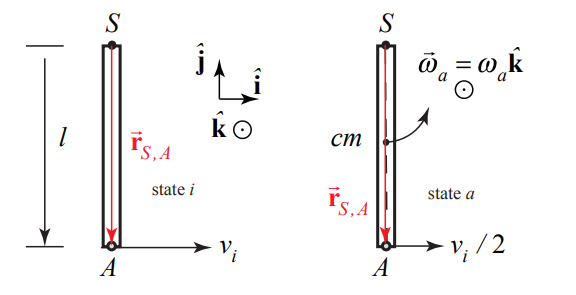
In order to calculate the angular momentum we draw a diagram showing the momentum of the object and the angular speed of the rod in (Figure 19.22). The angular momentum about \(S\) immediately before the collision is

\begin{equation}\overrightarrow{\mathbf{L}}_{S, i}^{\mathrm{sys}}=\overrightarrow{\mathbf{r}}_{S, 1} \times m_{1} \overrightarrow{\mathbf{v}}_{i}=l(-\hat{\mathbf{j}}) \times m_{1} v \hat{\mathbf{i}}=\operatorname{lm}_{1} v \hat{\mathbf{k}}\end{equation}

The angular momentum about \(S\) immediately after the collision is

\begin{equation}\overrightarrow{\mathbf{L}}_{S, a}^{\mathrm{yys}}=\overrightarrow{\mathbf{r}}_{S, 1} \times m_{1} \overrightarrow{\mathbf{v}}_{i} / 2+I_{S} \overrightarrow{\boldsymbol{\omega}}_{a}=l(-\hat{\mathbf{j}}) \times m_{1}\left(v_{i} / 2\right) \hat{\mathbf{i}}+I_{s} \omega_{a} \hat{\mathbf{k}}=\left(l m_{1} v_{i} / 2\right) \hat{\mathbf{k}}+I_{s} \omega_{a} \hat{\mathbf{k}}\end{equation}

Therefore the condition that the angular momentum about \(S\) is constant during the collision becomes

\begin{equation}\operatorname{lm}_{1} v_{i} \hat{\mathbf{k}}=\left(\operatorname{lm}_{1} v_{i} / 2+I_{s} \omega_{a}\right) \hat{\mathbf{k}}\end{equation}

We can solve for the angular speed immediately after the collision

\begin{equation}\omega_{a}=\frac{\operatorname{lm}_{1} v_{i}}{2 I_{S}}\end{equation}

\begin{equation}\omega_{a}=\frac{l m_{1} v_{i}}{2 I_{S}}\end{equation}

By the parallel axis theorem the moment of inertial of a uniform rod about the pivot point is

\begin{equation}I_{S}=m_{2}(l / 2)^{2}+I_{c m}=(1 / 4) m_{2} l^{2}+(1 / 12) m_{2} l^{2}=(1 / 3) m_{2} l^{2}\end{equation}

Therefore the angular speed immediately after the collision is

\begin{equation}\omega_{2}=\frac{3 m_{1} v_{i}}{2 m_{2} l}\end{equation}

Figure 19.23 Energy diagram for transition from state a to state f .

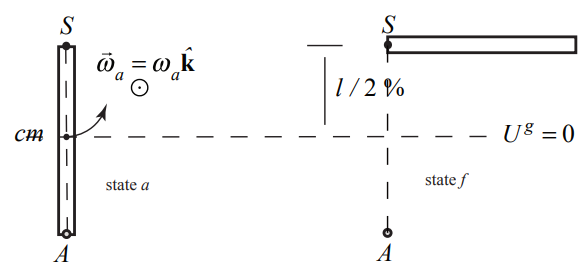
For the transition from state a to state f , we know that the gravitational force is conservative and the pivot force does no work so mechanical energy is constant.

\begin{equation}E_{a}^{m e c h}=E_{f}^{m e c h}\end{equation}

We draw an energy diagram only for the rod because the kinetic energy for the particle is not changing between states a and f , (Figure 19.23), with a choice of zero for the potential energy at the center of mass. The mechanical energy of the rod and particle immediately after the collision is

\begin{equation}E_{a}^{m e c h}=\frac{1}{2} I_{S} \omega_{a}^{2}+\frac{1}{2} m_{1}\left(v_{i} / 2\right)^{2}\end{equation}

Using our results for the moment of inertia \(I_{S}\) (Equation (19.5.39)) and \(\omega_{2}\) (Equation (19.5.40)), we have that

\begin{equation}E_{a}^{\text {mech}}=\frac{1}{2}(1 / 3) m_{2} l^{2}\left(\frac{3 m_{1} v_{i}}{2 m_{2} l}\right)^{2}+\frac{1}{2} m_{1}\left(v_{i} / 2\right)^{2}=\frac{3 m_{1}^{2} v_{i}^{2}}{8 m_{2}}+\frac{1}{2} m_{1}\left(v_{i} / 2\right)^{2}\end{equation}

The mechanical energy when the rod just reaches the ceiling when the final angular speed is zero is then

\begin{equation}E_{f}^{m e c h}=m_{2} g(l / 2)+\frac{1}{2} m_{1}\left(v_{i} / 2\right)^{2}\end{equation}

Then the condition that the mechanical energy is constant becomes

\begin{equation}\frac{3 m_{1}^{2} v_{i}^{2}}{8 m_{2}}+\frac{1}{2} m_{1}\left(v_{i} / 2\right)^{2}=m_{2} g(l / 2)+\frac{1}{2} m_{1}\left(v_{i} / 2\right)^{2}\end{equation}

We can now solve Equation (19.5.42) for the initial speed of the object

\begin{equation}v_{i}=\frac{m_{2}}{m_{1}} \sqrt{\frac{4 g l}{3}}\end{equation}

We now return to the transition from state i to state a . and determine the constraint on the mass ratio in order for the collision to be elastic. The mechanical energy before the collision is

\begin{equation}E_{i}^{m e c h}=\frac{1}{2} m_{1} v_{i}^{2}\end{equation}

If we impose the condition that the collision is elastic then

\begin{equation}E_{i}^{m e c h}=E_{a}^{m e c h}\end{equation}

Substituting Equations (19.5.41) and (19.5.44) into Equation (19.5.45) yields

\begin{equation}\frac{1}{2} m_{1} v_{i}^{2}=\frac{3 m_{1}^{2} v_{i}^{2}}{8 m_{2}}+\frac{1}{2} m_{1}\left(v_{i} / 2\right)^{2}\end{equation}

This simplifies to

\begin{equation}\frac{3}{8} m_{1} v_{i}^{2}=\frac{3 m_{1}^{2} v_{i}^{2}}{8 m_{2}}\end{equation}

Hence we can solve for the mass ratio necessary to ensure that the collision is elastic if the final speed of the object is half it’s initial speed

\begin{equation}\frac{m_{2}}{m_{1}}=1\end{equation}

Notice that this mass ratio is independent of the initial speed of the object.